How to Simplify Fractions
A fraction is considered to be “simplified” when it is expressed in the lowest term. That means the only common divisor between the numerator and denominator is [latex]1[/latex], and no other.
METHODS IN SIMPLIFYING FRACTIONS
Method 1: Simplify Fractions by Repeated Division
- Keep dividing the numerator and denominator by a common divisor until such time that the only remaining common divisor is [latex]1[/latex].
- Although there is no right way which common divisor to use in the beginning, I would suggest using the first five ([latex]5[/latex]) prime numbers in order as possible common divisor:
[latex]2[/latex], [latex]3[/latex], [latex]5[/latex], [latex]7[/latex], [latex]11[/latex], …
Method 2: Simplify Fractions Using the Greatest Common Factor
- Find the greatest common factor (GCF) of the numerator and denominator.
- Divide the top and bottom numbers of the fraction by the GCF to reduce to the lowest term.
- You can find the GCF either by trial and error when the numbers are relatively small, or by using Prime Factorization.
This is a simple illustration showing the fraction [latex]\Large{8 \over {12}}[/latex] is being reduced to its simplest form. Can you see a pattern?
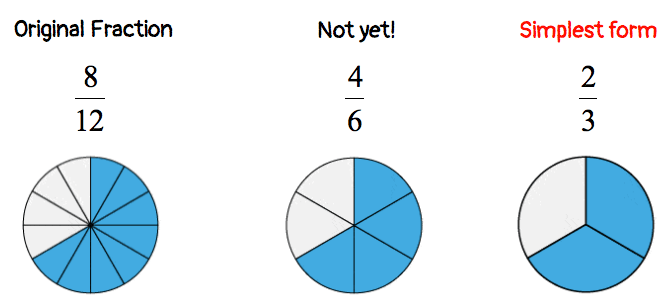
Let’s go over a few more examples with detailed explanations.
Examples of How to Simplify Fractions
Example 1: Simplify the fraction below.
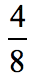
Simplify using Method 1: Repeated Division Method
It is obvious that [latex]1[/latex] is not the only common divisor between the numerator and denominator. Since they are both even numbers, they must be divisible by [latex]2[/latex].
- Divide the top and bottom by [latex]2[/latex]. Here’s what we got after doing so.
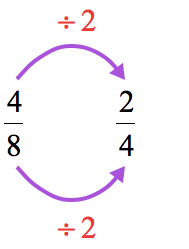
The output fraction after dividing the top and bottom by [latex]2[/latex] is [latex]\Large{2 \over 4}[/latex]. Can we stop here? Not yet! They can still be reduced by a second division of [latex]2[/latex].
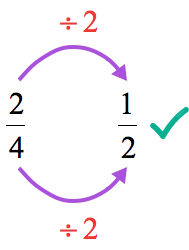
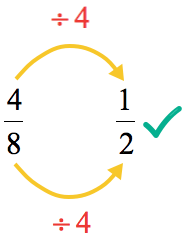
- Divide again the top and bottom by [latex]2[/latex]. The answer is [latex]\Large{1 \over 2}[/latex] (as the simplest form of [latex]\Large{4 \over 8}[/latex] because the only divisor of its numerator and denominator is [latex]1[/latex].
Simplify using Method 2: Greatest Common Factor Method
In the above solution using repeated division, we have simplified [latex]\Large{4 \over 8}[/latex] by dividing its numerator and denominator two times by the number [latex]2[/latex]. But wait! Is there a shortcut? Some of you may have observed that using a common divisor of [latex]4[/latex] can directly simplify it with a single step!
In fact, the Greatest Common Factor (GCF) of this fraction is [latex]4[/latex] because it is the LARGEST number that evenly divides the numerator and denominator. Because the numbers are small, the GCF can be determined by trial and error.
Example 2: Simplify the fraction below.
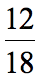
Simplify using Method 1: Repeated Division Method
Start simplifying using the first few prime numbers ([latex]2[/latex], [latex]3[/latex], [latex]5[/latex], [latex]7[/latex], [latex]11[/latex], etc).
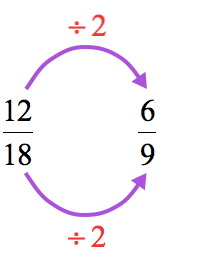
- Divide the top and bottom numbers by the first prime number which is [latex]2[/latex].
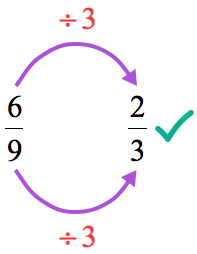
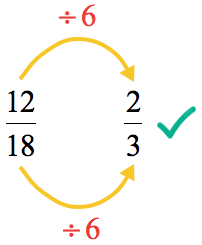
- We still have a common divisor! Divide the top and bottom by the next larger prime number which is [latex]3[/latex]. We should get the final answer after this step.
Simplify using Method 2: Greatest Common Factor Method
To find the greatest common divisor, we are going to perform prime factorization on each number. Next, identify the common factors between them. Finally, multiply the common factors to get the required GCF that can simplify the fraction.
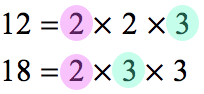
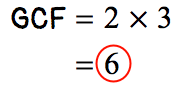
Since GCF = [latex]6[/latex], use this number to divide the numerator and denominator to get the answer in a single step.
Example 3: Simplify the fraction below.
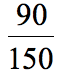
Simplify using Method 1: Repeated Division Method
We can start testing numbers [latex]2[/latex], [latex]3[/latex], [latex]5[/latex], etc. to simplify this. But there is an obvious divisor that stands out! Since both numbers end with zero, they should be divisible by [latex]10[/latex].
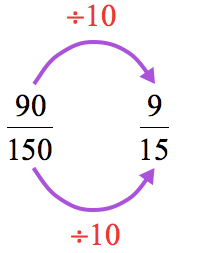
Now, [latex]2[/latex] can’t divide both and so try [latex]3[/latex].
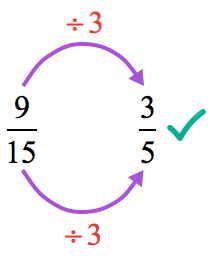
Simplify using Method 2: Greatest Common Factor Method
Prime factorize each number and get the product of the common factors to obtain the needed GCF.
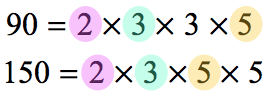
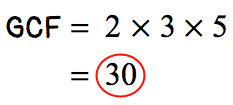
Simplify the given fraction in one-step using the divisor GCF = [latex]30[/latex].
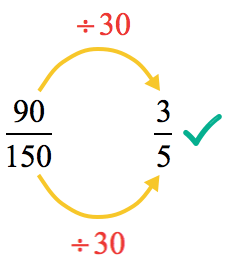
Example 4: Simplify the fraction below.
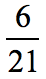
Solution:
Divide the numerator and denominator by a common divisor of [latex]3[/latex].
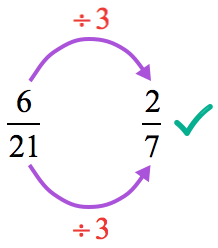
Example 5: Simplify the fraction.
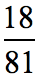
Solution:
Simplify using the repeated division method.
- Divide both numerator and denominator by [latex]3[/latex], two times!
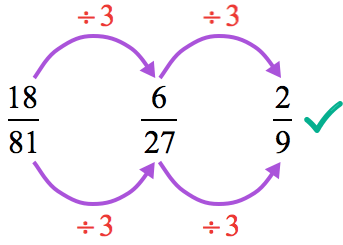
Example 6: Simplify the fraction below.
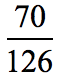
Solution:
Simplify this fraction by the greatest common factor method.
- Find the GCF by prime factoring both the numerator and denominator. Identify the common factors. Multiply them together to get the required GCF.
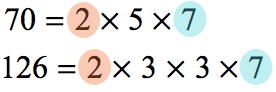
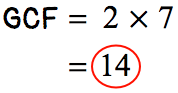
- After determining the GCF, divide the numerator and denominator to get the final answer.
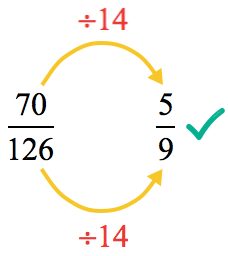
Example 7: Simplify the fraction below.
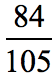
Solution:
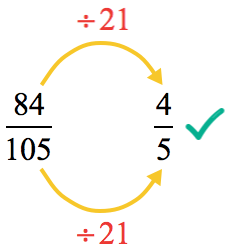
Find the greatest common factor between the numerator and denominator, and use this number to simplify the fraction.
- Determine the GCF
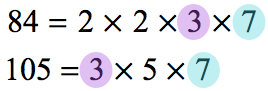
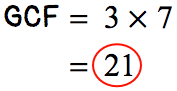
- Divide the numerator and denominator by GCF = [latex]21[/latex].
You may also be interested in these related math lessons or tutorials:
Adding and Subtracting Fractions with the Same Denominator
Add and Subtract Fractions with Different Denominators
Multiplying Fractions
Dividing Fractions
Equivalent Fractions
Reciprocal of a Fraction
