Writing and Identifying Equivalent Fractions

Fractions that are the same in value but “look” different are known as equivalent fractions. How can that be? As long as you multiply or divide the top and bottom of a fraction by the same nonzero whole number, the resulting fraction will be equivalent to the original.

Examples of Showing or Converting Equivalent Fractions

Example 1: Are the fractions below equivalent to each other?

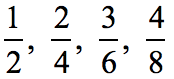
If we model all these fractions as the shaded parts of circles with the same size but subdivided into different equal parts, it becomes obvious that all colored regions occupy the same amount of area.

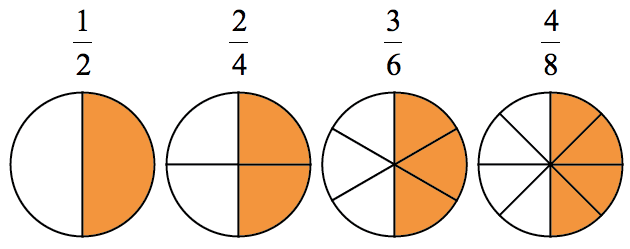
an illustration showing 1/2 as a circle divided into two equal parts with one part shaded, 2/4 as a circle divided into four equals parts with two parts shaded, 3/6 as a circle divided into six equal parts with three parts shaded, and finally 4/8 as a circle divided into eight equal parts with four parts shaded. note that 1/2, 2/4, 3/6, and 4/8 are equivalent fractions.

This is our visual/geometric “proof” why they are equivalent fractions.

Example 2: Are the fractions below equivalent?

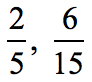
There are two ways we can show why these fractions are equivalent using some arithmetic.

One way is to start with [latex]{2 \over 5}[/latex] and multiply its top and bottom by [latex]3[/latex] to get the target fraction [latex]{6 \over 15}[/latex]

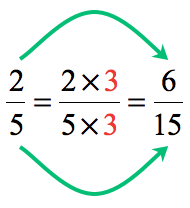
when we multiply both the numerator and denominator of 2/5 by 3, we get 6/15. thus, 2/5 and 6/15 are equivalent fractions.

Another way is to reverse the order. I start with [latex]{6 \over 15}[/latex] and divide its top and bottom by [latex]3[/latex] to arrive at [latex]{2 \over 5}[/latex]

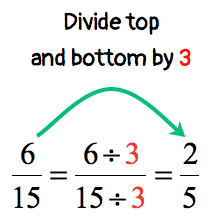
when we divide the numerator and denominator of 6/15 both by 3 we get 2/5. that is why 6/15 and 2/5 are equivalent fractions.

Therefore, fractions [latex]{2 \over 5}[/latex] and [latex]{6 \over 15}[/latex] are equivalent fractions!

In addition, here are the two fractions represented in circles having the same size but with different equal subdivisions. The two seemingly different fractions occupy the same area.

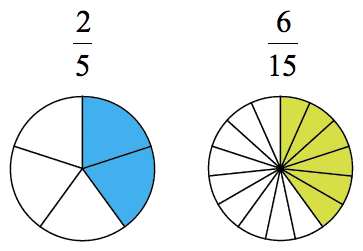
2/5 is represented by a circle divided into five equal parts with two parts shaded. similarly. 6/15 is shown as a circle divided into fifteen equal parts with six parts shaded. since 2/5 and 6/15 have the same amount of shaded area, therefore they are equivalent fractions.

This is how it looks when they overlap.

animated gif showing that two fifths (2/5) and six fifteenths (6/15) have the same shaded area thus they are equivalent.

Example 3: Show that the fractions below are equivalent fractions.

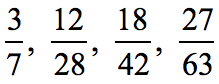
The strategy is to pick any of the four fractions and using some arithmetic, transform it into the other three fractions. For this example, I would pick the smallest fraction which is [latex]{3 \over 7}[/latex].

Step 1: Convert [latex]{3 \over 7}[/latex] to [latex]{12 \over 28}[/latex] to show that they are equivalent fractions.

Multiply [latex]{3 \over 7}[/latex] by [latex]{4 \over 4}[/latex] to get [latex]{12 \over 28}[/latex].

Thus,

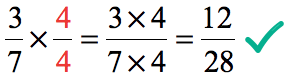
multiplying both the numerator and denominator of 2/7 by 4 we get 12/28. that means 3/7 is equivalent to 12/28.

Step 2: Convert [latex]{3 \over 7}[/latex] to [latex]{18 \over 42}[/latex] to show that they are equivalent fractions.

Multiply [latex]{3 \over 7}[/latex] by [latex]{6 \over 6}[/latex] to get [latex]{18 \over 42}[/latex].

Thus,

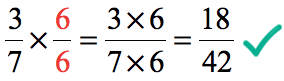
if we multiply the top and bottom of the fraction 3/7 by 6 we get 18/42 which implies that 3/7 is equivalent to 18/42.

Step 3: Convert [latex]{3 \over 7}[/latex] to [latex]{27 \over 63}[/latex] to show that they are equivalent fractions.

Multiply [latex]{3 \over 7}[/latex] by [latex]{9 \over 9}[/latex] to get [latex]{27 \over 63}[/latex].

Thus,

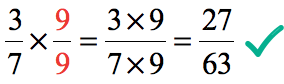
when 3/7 is multiplied by 9 both on its numerator and denominator we obtain the fraction 27/63. it means that 3/7 is equivalent to 27/63.

Since [latex]{3 \over 7}[/latex] can be converted into [latex]{12 \over 28}[/latex], [latex]{18 \over 42}[/latex] and [latex]{27 \over 63}[/latex], all of them are equivalent fractions.

Example 4: Show that the fractions below are equivalent fractions.

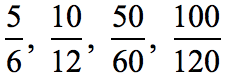
This time, I will pick the largest fraction which is [latex]{{100} \over {120}}[/latex] and work myself backward by transforming it to the other three fractions with lesser values. Since the values would be going down, it makes sense to use division instead of multiplication.

Step 1: Transform [latex]{100 \over 120}[/latex] to [latex]{50 \over 60}[/latex].

Divide both the top and bottom of [latex]{100 \over 120}[/latex] by [latex]2[/latex] to obtain [latex]{50 \over 60}[/latex].

Thus,

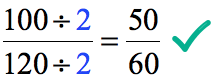
100/120 is equivalent to 50/60 since they can be both reduced to 5/6.

Step 2: Transform [latex]{100 \over 120}[/latex] to [latex]{10 \over 12}[/latex].

Divide both the top and bottom of [latex]{100 \over 120}[/latex] by [latex]10[/latex] to obtain [latex]{10 \over 12}[/latex].

Thus,

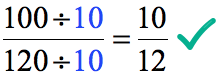
if you divide the numerator and denominator of the fraction 100/120 by 10 we obtain 10/12. this shows that 100/120 is equivalent to 10/12.

Step 3: Transform [latex]{100 \over 120}[/latex] to [latex]{5 \over 6}[/latex].

Divide both the top and bottom of [latex]{100 \over 120}[/latex] by [latex]20[/latex] to obtain [latex]{5 \over 6}[/latex].

Thus,

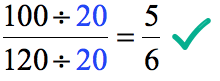
dividing the numerator and denominator of 100/120 by 10 we get 5/6. this implies that 100/120 and 5/6 are equivalent fractions.

This can be a short arithmetic “proof” demonstrating that they are indeed equivalent fractions.

There is also an easier way to show that two fractions are equivalent. We may call it the “Cross-Multiplication” Rule.

Cross-Multiplication Rule

Here are the steps:

Step 1: To check if [latex]{a \over b}[/latex] and [latex]{c \over d}[/latex] are equivalent fractions, set them equal to each other.

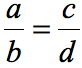
Step 2: Perform the cross-multiplication procedure. The diagram below should help.

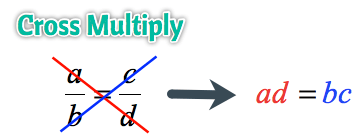
Multiply the left numerator to the right denominator. Write it as [latex]ad[/latex].

Then write the equal symbol ([latex]=[/latex]).

Finally, multiply the left denominator to the right numerator. Write it as [latex]bc[/latex].

Step 3: If [latex]ad=bc[/latex] is a true statement then [latex]{a \over b}[/latex] and [latex]{c \over d}[/latex] are equivalent fractions. Otherwise, if [latex]ad \ne bc[/latex] then the two fractions are not equivalent.

Examples of How to Apply the Cross-Multiplication Rule to Verify if the Two Given Fractions are Equivalent

Example 5: Are the fractions below equivalent?

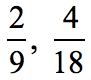
The cross products are equal. This means that they are equivalent fractions.

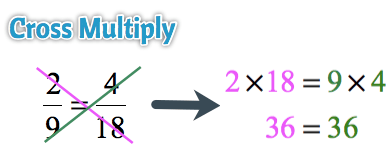
Example 6: Are the fractions below equivalent?

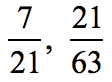
These two fractions may seem to be totally different in value. But the cross multiplication rule should reveal their equivalency.

when you cross multiply the proportion 7/21 = 21/63 you will get 7 x 63 = 21 x 21 = 441

Yes, they are indeed equivalent fractions!

You might also be interested in:

Adding and Subtracting Fractions with the Same Denominator
Add and Subtract Fractions with Different Denominators
Multiplying Fractions
Dividing Fractions
Simplifying Fractions
Reciprocal of a Fraction