Add and Subtract Fractions with the Same or Like Denominator

When adding or subtracting fractions, consider the problem simple if the denominators are equal or the same. The rules are outlined below.

Steps on How to Add and Subtract Fractions with the Same Denominator

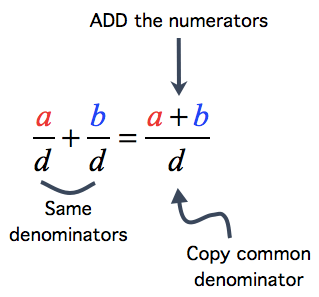
To ADD fractions with like or the same denominator, simply add the numerators then copy the common denominator. Always reduce your final answer to its lowest term.

let a, b, and d be integers but b ≠ 0. (a/d) + (b/d) = (a+b)/d. we can simply add the numerators because they have the same or like denominator which is d.

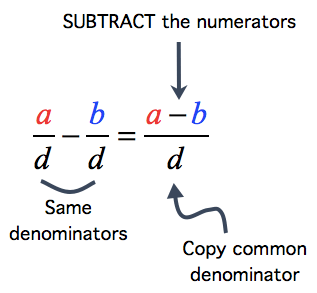
To SUBTRACT fractions with like or the same denominator, just subtract the numerators then copy the common denominator. Always reduce your final answer to its lowest term.

we assume here also that a, b and d are integers but b ≠ 0. subtracting two fractions with the same denominator simply means to subtract the numerators then copy the like denominator which is d. so we have (a/d) - (b/d) = (a-b)/d.

Examples of Adding and Subtracting Fractions with Like Denominator

Example 1: Add the fractions.

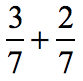
sum of three sevenths and two sevenths or (3/7) + (2/7)

The denominators of the two fractions are both 7. Since they have the same denominator, we can easily add these fractions by adding their numerators and copying the common denominator which is 7.

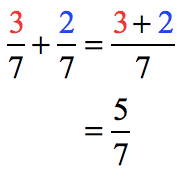
to add 3/7 and 2/7, we add their numerators and copy the like denominator. So we have, (3/7) + (2/7) = (3+2)/7 = 5/7

We can also show the addition process using circles.

The first fraction [latex]\Large{3 \over 7}[/latex] can be represented by a circle divided equally into seven parts with three pieces shaded in red.

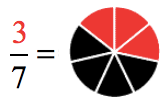
the fraction three sevenths or 3/7 can be represented by a circle divided into seven equal parts and shading only the three equal parts to represent the numerator.

Observe: The numerator tells us how many areas are shaded while the denominator tells us how many equal parts the circle is divided.

In the same manner, the second fraction [latex]\Large{2 \over 7}[/latex] looks like this:

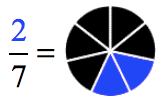
when a circle is equally divided into seven equal portions/parts, and we shade only two of them, we can describe it in fraction as two over sevenths or 2/7.

Since the two circles are both divided into seven (7) equal parts, we should be able to overlap them. The new circle after addition has five (5) shaded regions which are the accumulation of both the red and blue pieces.

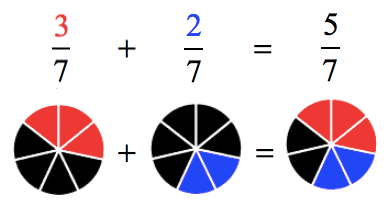
this illustration shows the addition of two fractions namely 3/7 and 2/7 with a visual model using shaded circles. (3/7) added to (2/7) is equal to 5/7 because we get the sum of the numerator and copying the common denominator.

Example 2: Add the fractions.

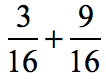
find the sum of three-sixteenths and nine-sixteenths or (3/16) + (9/16)

Let’s combine these fractions using the addition rule. Again, add the numerators then copy the common denominator.

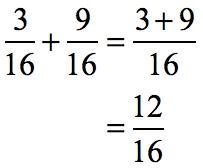
After you add fractions, always find the opportunity to simplify the result by reducing it to the lowest term. We can do so by dividing both the numerator and denominator by their greatest common divisor.

Common divisor is a nonzero whole number that can evenly divide two or more numbers.
Greatest Common Divisor (GCD) is the largest number among the common divisors of two or more numbers.

The numerator and denominator obviously have a common divisor of 2. However, is there a number larger than 2 that can also evenly divide both of them?

Yes, there is! The number 4 is the greatest common divisor of 12 and 16. Therefore, we will use this number to reduce the fraction to its lowest term.

Divide the top and bottom by the GCD = 4 to get the final answer.

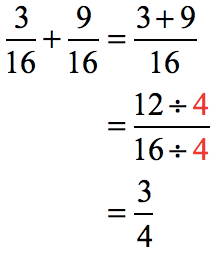
(3/16) + (9/16) = (3+9)/16 = 12/16. To reduce this fraction to its simplest form, we divide both the numerator and denominator by 4 to get the final answer of 3/4.

Example 3: Add the fractions.

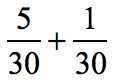
five over thirty added to one over thirty, (5/30) + (1/30)

Solution:

Since the denominators of the two fractions are equal, add the numerators and copy the common denominator.

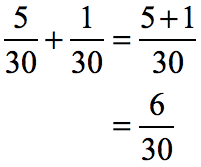
The top and bottom numbers of the fraction are divisible by 2 and 6. However, we always want the largest common divisor to reduce the fraction to its lowest term. Thus, the GCD = 6.

Divide the top and bottom numbers by 6.

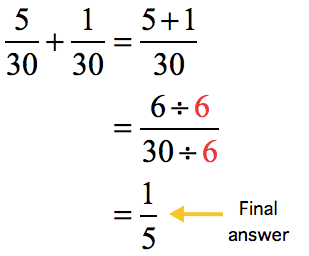
(5/30) + (1/30) = (5+1)/30 = 6/30. To reduce 6/30 to its simplest form, we divide the numerator and denominator by 6 to get the final answer of 1/5.

Example 4: Add the fractions.

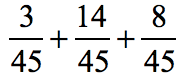
Solution:

All three fractions have the same denominator. We will add as usual.

Get the sum of the three numerators then copy the common denominator.

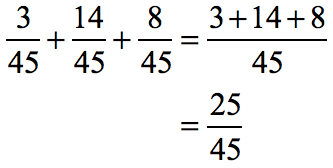
(3/45) + (14/45) + (8/45) = (3+14+8)/45 = 25/45

The greatest common divisor between the numerator and denominator is 5.

Divide top and bottom by 5.

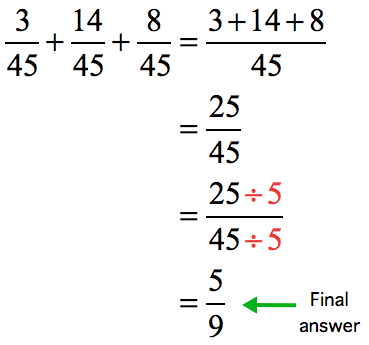
(3/45) + (14/45) + (8/45) = (3+14+8)/45 = 25/45. To reduce 25/45 to its simplest form, we divide both the numerator and denominator by 5 to get the final answer of 5/9.

Example 5: Subtract the fractions.

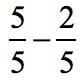
five-fifths minus two-fifths or (5/5) - (2/5)

This time around, we are going to subtract the numerators instead of adding them.

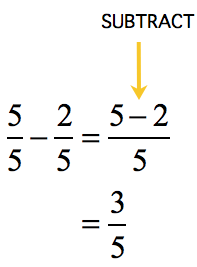
to find the difference between 5/5 and 2/5, we subtract the numerators then copy the common denominator. This can be written as (5/5) - (2/5) = (5-2)/5 = 3/5. This is the final answer because the greatest common divisor of the numerator and denominator 3 and 5, respectively, is 1.

Looking at the result after subtraction, the only common divisor between the numerator and denominator is 1. Thus, the final answer remains as [latex]\Large{{3 \over 5}}[/latex]. Think about it, dividing the top and bottom by 1 won’t change the value of the fraction.

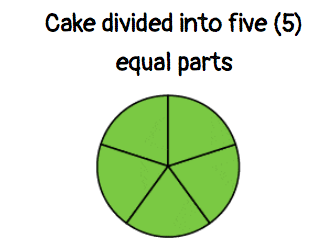
Suppose you have a green cake. And you cut it into 5 equal portions. This can be represented as a fraction which is [latex]\Large{{5 \over 5}}[/latex].

a cake divided into five equal parts or portions

If you ate two slices of the cake ( [latex]\Large{- {2 \over 5}}[/latex] ), you should have three leftover pieces ( [latex]\Large{{3 \over 5}}[/latex] ).

The plate should look something like this.

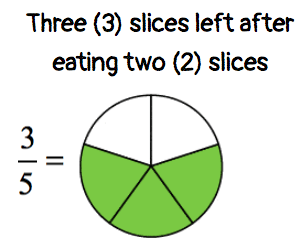
an illustration showing three pieces left after eating two slices of cake which also can be written in fraction as 3/5.

Example 6: Subtract the fractions.

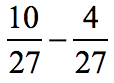
ten over twenty-seven minus 4 over twenty-seven or (10/27) - (4/27)

The two fractions have the same denominator which means we should be able to easily subtract their numerators.

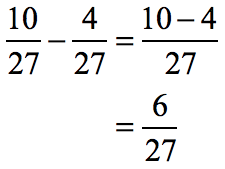
The answer can still be further simplified using a common divisor of 3. So, divide the numerator and denominator by 3 to reduce the fraction to its lowest terms.

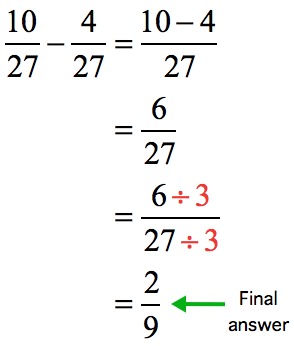
(10/27) - (4/27) = (10-4)/27 = 6/27. To reduce 6/27 to its simplest form, we divide the top and bottom numbers by the greatest common divisor which is 3, to get the final answer of 2/9.

Example 7: Subtract the fractions.

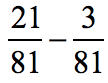
twenty-one over eighty-one minus three over eighty-one or (21/81) - (3/81)

Solution:

Since the denominators of the two fractions are equal, subtract their numerators then copy the common denominator.

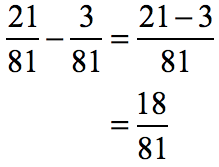
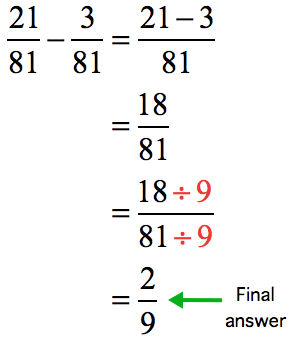
The numerator and denominator are divisible by 3 and 9. However, we always want the largest common divisor to reduce the fraction to its lowest term. Thus, the GCD = 9.

Divide the top and bottom numbers by 9.

(21/81) - (3/81) = (21-3)/81 = 18/81. Divide both the numerator and denominator by 9 to reduce 18/81 to its simplest form. In doing so, we get 2/9 as the final answer.

Example 8: Subtract the fractions.

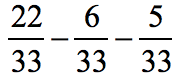
Solution:

Subtract the numerators, copy the common denominator, and reduce the resulting fraction to its lowest term using the GCD = 11.

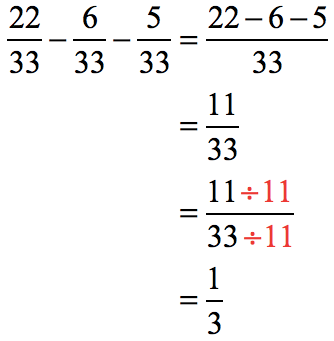
(22/33) - (6/33) - (5/33) = (22-6-5)/33 = 11/33. We then divide both the numerator and denominator of 11/33 by 11 to reduce it to its simplest form. Our final answer is 1/3.

You might also be interested in:

Add and Subtract Fractions with Different Denominators
Multiplying Fractions
Dividing Fractions
Simplifying Fractions
Equivalent Fractions
Reciprocal of a Fraction