Multiplying Fractions
To multiply fractions is as easy as following the 3 suggested steps below. It’s understood that no fraction can have a denominator of zero [latex]\color{red}0[/latex] because it will be an undefined term.
Steps in Multiplying Fractions
Given two fractions with nonzero denominators:
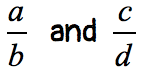
Step 1: Multiply the numerators.
- This will be the numerator of the “new” fraction.
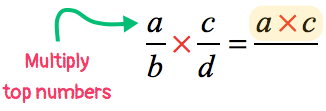
Step 2: Multiply the denominators.
- This will be the denominator of the “new” fraction.
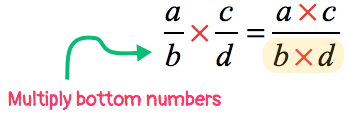
Step 3: Simplify the resulting fraction by reducing it to the lowest term, if needed.
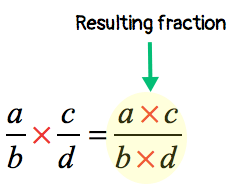
Before we go over some examples, there are other ways to mean multiplication.
- Dot symbol as a multiplication operator
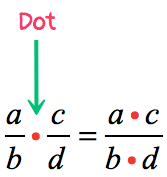
- Parenthesis as a multiplication operator
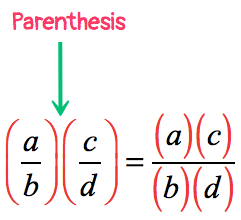
Examples of How to Multiply Fractions
Example 1: Multiply.
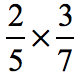
Multiply the numerators of the fractions.
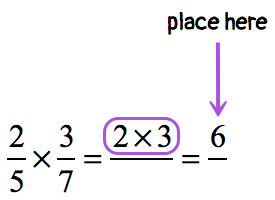
Similarly, multiply the denominators together.
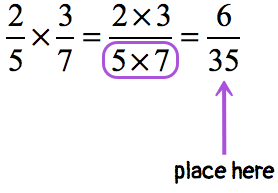
The resulting fraction after multiplication is already in its reduced form since the Greatest Common Divisor of the numerator and denominator is [latex]\color{blue}+1[/latex]. This becomes our final answer!
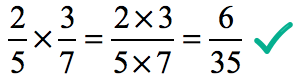
Example 2: Multiply.
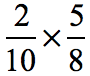
Step 1: Multiply the top numbers.
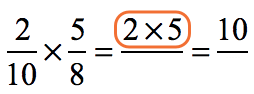
Step 2: Multiply the bottom numbers.
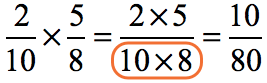
Step 3: Simplify the answer by reducing to the lowest term.
Divide the top and bottom by its Greatest Common Factor (GCF) which is [latex]10[/latex].
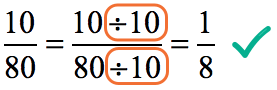
Example 3: Multiply.
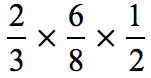
You may encounter a problem where you will be asked to multiply three fractions.
The general idea remains the same just like when you multiply two fractions, as shown in previous examples.
Step 1: Calculate the product of the numerators.
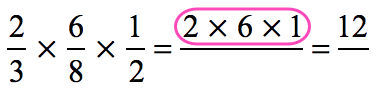
Step 2: Compute the product of the denominators.
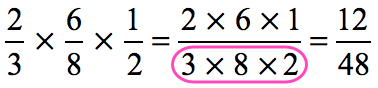
Step 3: Reduce the fraction to its simplest form.
Divide both the numerator and denominator by the greatest common divisor that is [latex]12[/latex].
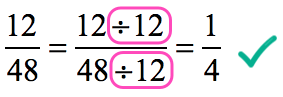
Example 4: Multiply a whole number by a fraction.
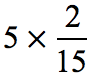
When you multiply a whole number to a fraction, think of the whole number as a fraction with a denominator of [latex]1[/latex]. Since
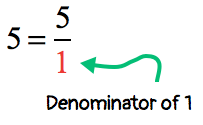
Therefore, we can rewrite the original problem as [latex]{5 \over 1} \times {2 \over {15}}[/latex]. With that, it should allow us to multiply the fractions as usual.
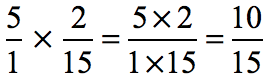
Finally, reduce the answer by dividing the numerator and denominator by [latex]5[/latex].
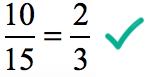
Example 5: Multiply.
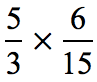
Step 1: Multiply the numerators
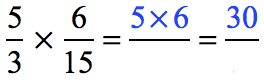
Step 2: Multiply the denominators
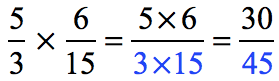
Step 3: Reduce the answer to the lowest term by dividing the top and bottom by the Greatest Common Divisor which is [latex]15[/latex].
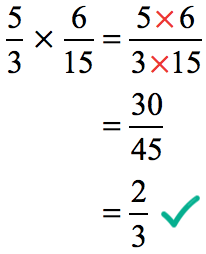
Example 6: Multiply.
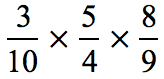
Solution:
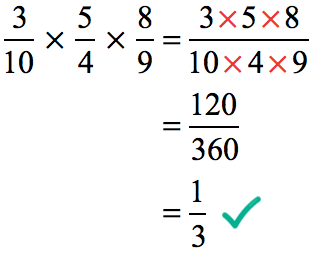
Example 7: Multiply.
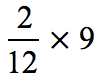
Solution:
Rewrite the whole number [latex]9[/latex] with a denominator of [latex]1[/latex]. Thus, [latex]\large{9 = {9 \over 1}}[/latex]
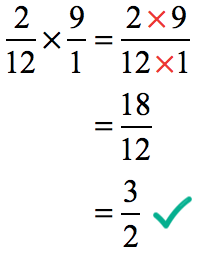
You may also be interested in these related math lessons or tutorials:
Adding and Subtracting Fractions with the Same Denominator
Add and Subtract Fractions with Different Denominators
Dividing Fractions
Simplifying Fractions
Equivalent Fractions
Reciprocal of a Fraction
