Divide Fractions by Converting to Multiplication of Fractions
To divide fractions, we need to know these 3 basic parts. Suppose we want to divide [latex]\Large{a \over b}[/latex] by [latex]\Large{c \over d}[/latex], the setup should look like this.
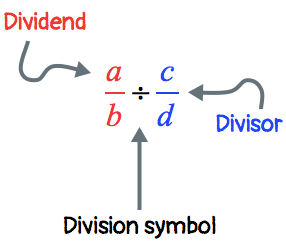
- Dividend – the number being divided or partitioned by the divisor. It is found to the left of the division symbol.
- Divisor – the number that is dividing the dividend. It is located to the right of the division symbol.
Now, apply the following simple steps to divide these fractions.
General Steps on How to Divide Fractions
- Step 1: Find the reciprocal of the divisor (second fraction) by flipping it upside down. The reciprocal of [latex]\Large {a \over b}[/latex] is [latex]\Large {d \over c}[/latex].
- Step 2: Multiply the dividend (first fraction) by the reciprocal of the divisor.
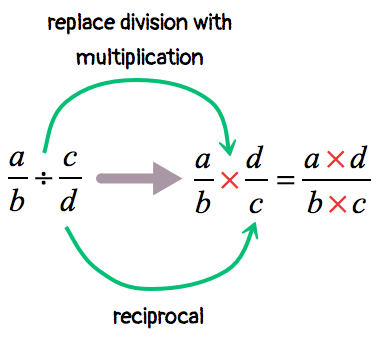
- Step 3: Simplify the “new” fraction that comes out after multiplication by reducing it to lowest term.
Examples of How to Divide Fractions
Example 1: Divide the fractions below.
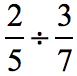
The reciprocal of the divisor (second fraction) is
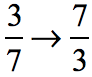
Multiply the dividend (first fraction) to the reciprocal of the divisor.
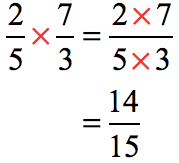
This is our final answer because the resulting fraction is already in its lowest term!
Example 2: Divide the fractions below.
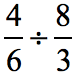
Sometimes you may encounter the phrase “inverse of a fraction”. That’s pretty much the same when we find the reciprocal of a fraction. So let’s go ahead and find the inverse of the divisor (second fraction).
The inverse of [latex]\Large{8 \over 3}[/latex] is just [latex]\Large{3 \over 8}[/latex].
Obviously, the next step is to find the product of the dividend and the inverse of the divisor.
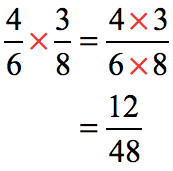
The resulting answer is not simplified yet because the numerator and denominator have a common divisor. Can you think of the common divisors of [latex]12[/latex] (numerator) and [latex]48[/latex] (denominator)?
If we do some trial and error, the possible common divisors of [latex]12[/latex] (numerator) and [latex]48[/latex] (denominator) are:
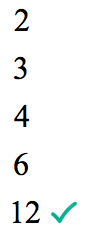
But we want the greatest common divisor to reduce our answer to the lowest term, which in this case is [latex]12[/latex].
- Divide the top and bottom by GCF =[latex]12[/latex] to get the final answer.
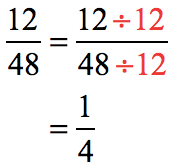
Example 3: Divide a fraction by a whole number, .
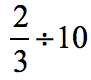
This time we have a fraction being divided by a whole number. Notice that any nonzero whole number can be rewritten with a denominator of [latex]1[/latex]. Therefore, the number [latex]10[/latex] is just [latex]\large10 = {{10} \over 1}[/latex]. In this form, it is easy to find its inverse or reciprocal.
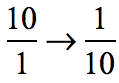
Now we are ready to divide by multiplying the dividend by the reciprocal of the divisor.
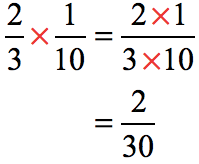
The greatest common divisor between the numerator and denominator is [latex]2[/latex]. That means, we can reduce it to the lowest term by dividing both the top and bottom numbers by [latex]2[/latex].
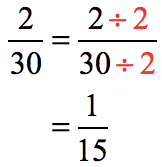
Example 4: Divide the fractions below.
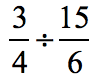
Solution:
Multiply the dividend (first fraction) by the reciprocal of the divisor (second fraction).
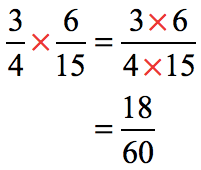
The greatest common divisor is [latex]6[/latex]. Use that to reduce the answer to the lowest term.
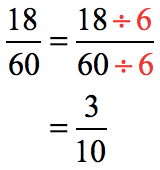
Example 5: Divide the fractions below.
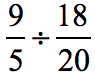
Solution:
Before we even divide the fractions, try to see if you can reduce the existing fractions to its lowest term. Observe that the divisor (second number) can be reduced using a common divisor of [latex]2[/latex].
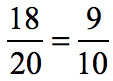
Rewriting the original problem with a reduced divisor, we have…
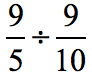
The fractions now are relatively smaller in size. Proceed with division by multiplying the dividend to the inverse of the divisor.
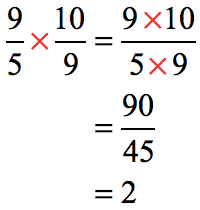
The final answer is reduced to a whole number. Great!
Example 6: Divide the fraction by a whole number.
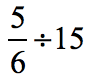
Solution:
The divisor can be rewritten with a denominator of [latex]1[/latex]. Thus, [latex]\large15 = {{15} \over 1}[/latex].
The problem becomes
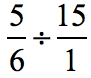
We are now ready to divide the fractions.
Multiply the dividend to the inverted divisor.
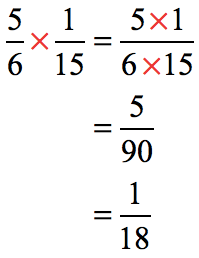
You may also be interested in these related math lessons or tutorials:
Adding and Subtracting Fractions with the Same Denominator
Add and Subtract Fractions with Different Denominators
Multiplying Fractions
Simplifying Fractions
Equivalent Fractions
Reciprocal of a Fraction
