Add & Subtract Fractions having Different Denominators

We need to take some extra steps to add or subtract fractions with different denominators. The general strategy is discussed further below. In this lesson, we will go over a few examples to ensure that you are comfortable with the procedure.

Steps How to Add or Subtract Fractions with Different Denominators

Step 1: Given two unlike fractions where the denominators are NOT the same.

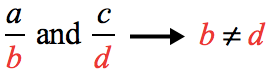
in a/b and c/d, it implies b is not the same as d

Step 2: Make the denominators the same by finding the Least Common Multiple (LCM) of their denominators. This step is exactly the same as finding the Least Common Denominator (LCD).

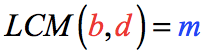
Least Common Multiple of b and d is equal to m, or LCM(b,d)=m

Step 3: Rewrite each fraction into its equivalent fraction with a denominator that is equal to the Least Common Multiple that you found in step #2.

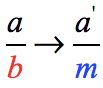
a/b is rewritten as a'/m
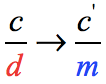
c/d is rewritten as c'/m

Step 4: Now, add or subtract the “new” fractions from step #3. Always reduce the answer to its lowest terms.

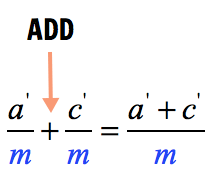
(a'/m)+(c'/m)=(a'+c')/m
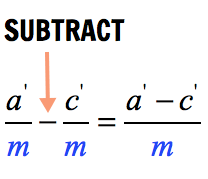
(a'/m)-(c'/m)=(a'-c')/m

Examples of Adding and Subtracting Fractions with Unlike Denominators

Example 1: Add the fractions with different denominators.

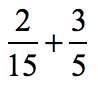
(2/15) + (3/5)

The two fractions have denominators that are not equal. We need to make them equal by finding their Least Common Multiple that will serve as their Least Common Denominator (LCD).

Start by listing the multiples of each denominator, and identify the least number that is common to both of them.

a table showing the first five multiples of the numbers 5 and 15. The LCM is found to be 15. We can write this as LCM (15, 5) = 15.

The first fraction already has a denominator equal to the LCM = 15 so we will leave it alone.

The second fraction requires some adjusting to make its denominator equal to 15. Do that by multiplying its numerator and denominator by the number 3.

  • Once their denominators are equal, add the fractions by adding their numerators and then copying the common denominator.
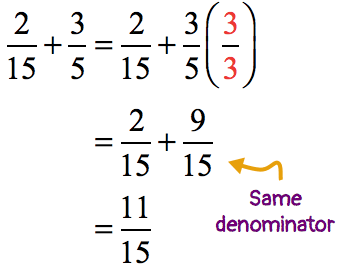
sum of fractions: (2/15)+(3/5)=11/15

The fraction [latex]{{11} \over {15}}[/latex] is our final answer because it is already in its lowest term.

Example 2: Add the fractions with different denominators.

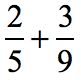
the sum of the fraction 2/5 and 3/9

We can’t add the two fractions just yet because they have different denominators, namely 5 and 9. Begin by listing their multiples and pick the smallest number that is common to both. This will become their common denominator.

a table showing the first few multiples of 5 and 9. It's obvious to see on the list that 45 is the least common multiple. Therefore, LCM (5, 9) = 45.

Now, convert each fraction to an equivalent fraction with the LCM as its denominator, then proceed with regular addition.

Look for the opportunity to reduce the answer to its lowest term. The numerator and denominator of [latex]{{33} \over {45}}[/latex] is divisible by 3.

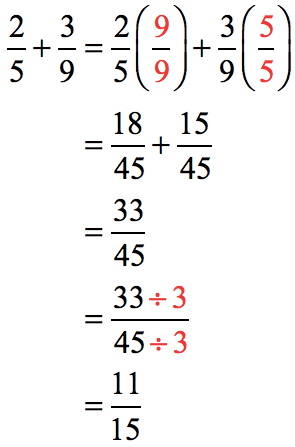
(2/5) + (3/9) = (2/5)(9/9) + (3/9)(5/5) = (18/45) + (15/45) = 33/45. We can simplify or reduce 33/45 to its lowest term by dividing the top and bottom by 3 to get 11/15.

Example 3: Add the fractions with different denominators.

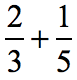
two-thirds plus one fifth or (2/3) + (1/5)

Sometimes there is no need to find the least common denominator by list method. We can immediately find it whenever the two numbers are both primes.

  • A prime number is a whole number greater than 1 that is divisible by 1 and itself.

Observe that the denominators 3 and 5 are primes. The LCD will simply be their product, that is, 3 x 5 = 15.

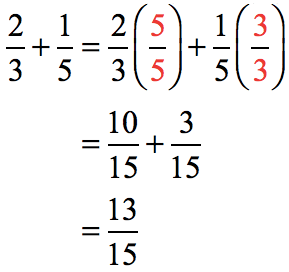
(2/3) + (1/5) = (2/3)(5/5) + (1/5)(3/3) = (10/15) + (3/15) = 13/15. So the final answer is 13 over 15.

Example 4: Add the fractions with different denominators.

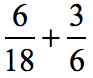
six eighteenths plus three sixths or (6/18) + (3/6)

Solution:

Find the least common multiple of the denominators.

a table that shows the first five multiples of the numbers 18 and 6. The LCM is obviously 18 as read from the list of multiples. We can also write this as LCM (18,6) = 18.

Make the necessary adjustments in the denominator and proceed as usual. Reduce your final answer to the lowest term.

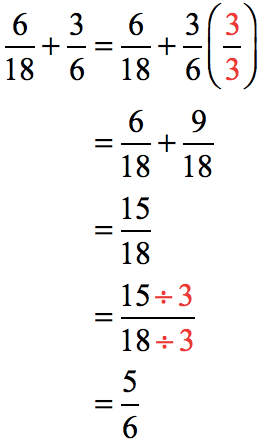
(6/18) + (3/6) = (6/18) + (3/6) (3/3) = (6/18) + (9/18) = 15/18. We can reduce 15/18 to its lowest term by dividing the numerator and denominator by 3. The final answer is 5/6.

Example 5: Add the fractions with different denominators.

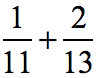
(1/11) + (2/13)

Solution:

Since the denominators 11 and 13 are both prime numbers, the least common denominator will be their product.

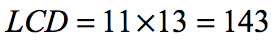
LCD = 11 x 13 = 143

Convert the current denominators of the two fractions into the LCD, and proceed with regular addition.

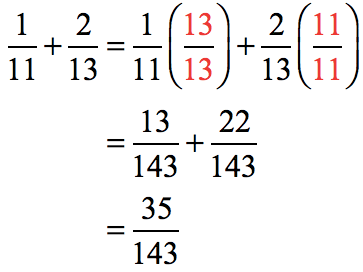
(1/11) + (2/13) = 1/11 (13/13) + 2/13 (11/11) = (13/143) + (22/143) = 35/143. The final answer is 35/143.

Example 6: Subtract the fractions with different denominators.

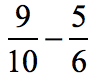
9 over 10 minus 5 over six or (9/10) - (5/6)

To subtract fractions with unequal denominators is very similar to addition.

Make their denominators equal using the concept of least common multiple. Then subtract their numerators accordingly.

this table shows the first nine multiples of the numbers 6 and 10. The first eight multiples of 6 are 6, 12, 18, 24, 30, 36, 42, and 48. While the first eight multiples of 10 are 10, 20, 30, 40, 50, 60, 70, and 80. Since the least common number on both lists is 30, the least common multiple of 10 and 6 is 30. This can be written as LCM (10, 6) = 30.

Rewrite each fraction to its equivalent fraction with a denominator equal to the LCM = 30, then subtract their numerators. Make sure to reduce your answer to the lowest term.

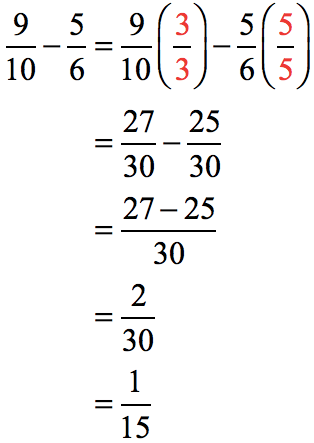
(9/10) - (5/6) = 9/10 (3/3) - 5/6 (5/5) = (27/30) - (25/30) = (27-25)/30 = 2/30 = 1/15

Example 7: Subtract the fractions with different denominators.

(6/7) - (3/5)

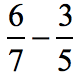
Since the denominators are both prime numbers, their LCM is just their product, thus 7 x 5 = 35.

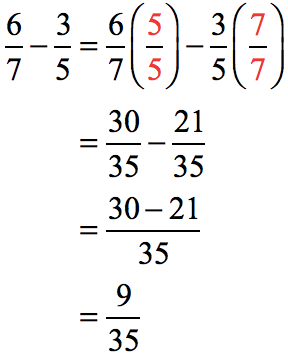
(6/7) - (3/5) = 6/7 (5/5) - 3/5 (7/7) = (30/35) - (21/35) = (30-21)/35 = 9/35

Example 8: Subtract the fractions with different denominators.

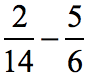
(2/14) - (5/6)

Solution:

Find the least common denominator by determining the LCM of the denominators.

this table shows the first seven multiples of 14 and 6. From the list of multiples, we can see that the LCM is 42. We can also write this as LCM (14, 6) = 42.

Rewrite the two fractions with a common denominator equal to the LCM = 42. Subtract their numerators, and reduce the answer to the lowest term if possible.

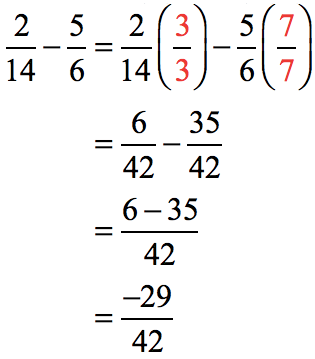
(2/14) - (5/6) = 2/14 (3/3) - 5/6 (7/7) = (6/42) - (35/42) = (6-35)/42 = (-29)/42

Example 9: Subtract the fractions with different denominators.

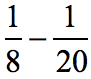
(1/8) - (1/20)

Solution:

Find the least common denominator by determining the least common multiple of the denominators.

here's a table that shows the first few multiples of the numbers 8 and 20. From the list, we can see that 40 is least common multiple. This can also be written as LCM (8, 20) = 40.

We make adjustments to the existing fractions to make their denominator equal to the LCD = 40. After doing so, subtract their numerators and copy the common denominator.

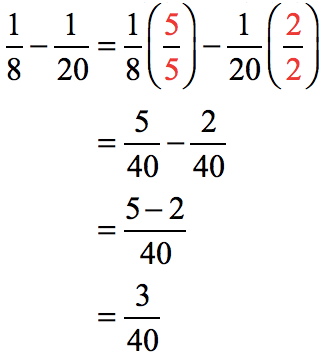
(1/8) - (1/20) = 1/8 (5/5) - 1/20 (2/2) = (5/40) - (2/40) = (5-2)/40 = 3/40. The final answer is 3/40 because this fraction is already in its simplest form.

You may also be interested in these related math lessons or tutorials:

Adding and Subtracting Fractions with the Same Denominator
Multiplying Fractions
Dividing Fractions
Simplifying Fractions
Equivalent Fractions
Reciprocal of a Fraction