Prime Factorization of an Integer

Prime Factorization of an Integer

The method of prime factorization is used to “break down” or express a given number as a product of prime numbers. More so, if a prime number occurs more than once in the factorization, it is usually expressed in exponential form to make it look more compact.

Otherwise, we will have a long list of prime numbers being multiplied together. In this lesson, I have prepared eight (8) worked examples to explain the process of factorization using Prime numbers.

Note: When I make mention of “numbers” here, I mean to say positive integers.

Definition of a Prime Number, and Examples and Non-examples of Prime Numbers

Let’s get started by defining first what a prime number is. Study both the examples and counterexamples of prime numbers carefully.

What is a Prime Number?

A prime number [latex]p[/latex] is a whole number greater than 1 that is only divisible by 1 and itself. Another way of saying it is a prime number has exactly two factors, namely: 1 and itself.

Examples of Prime Numbers:

  • The number 2 is a prime number because it is divisible only by 1 and 2 (itself)
  • The number 17 is a prime number because it has exactly two factors which are 1 and 17 (itself)
  • The number 31 is a prime number because it can only be divided by two numbers namely 1 and 31 (itself)

Examples of Numbers that are Not Prime:

  • The number 10 is not a prime number because it is divisible by 1, 5, and 10 (itself) therefore having more than two factors
  • The number 27 is not a prime number because it is divisible by more than two factors other than 1 and itself that includes 3 and 9
  • The number 49 is not a prime number because it can also be divided by 7 other than 1 and 49 (itself), thus having more than two factors

Now, I will explain the general steps involved in performing prime factorization of a given positive integer.

How to Perform Prime Factorization

Step 1: List down at least the first few prime numbers in increasing order. I will stop at 19 because this is large enough for the numbers in this tutorial that we will factorize.

2, 3, 5, 7, 11, 13, 17, 19 …

Step 2: For any given number, test if it is divisible by the smallest prime number which is 2. If the prime number 2 divides the given number evenly, then express it as factors:

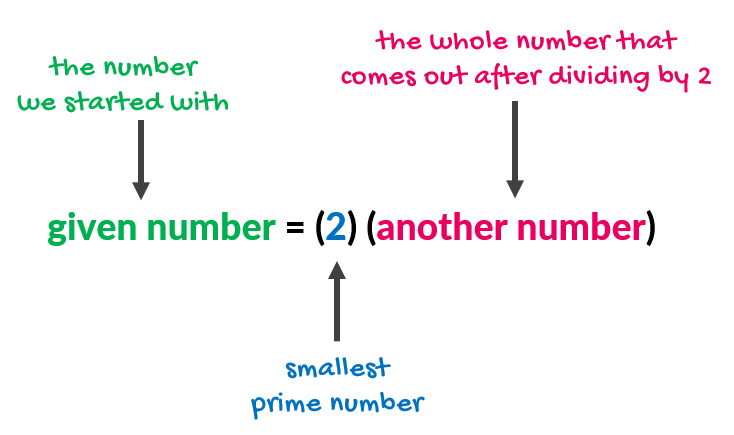
the given number is equal to 2 times another number; where the given number is the number we start with, two (2) is the smallest prime number, and another number is the whole number that comes out after dividing by 2. we can also write this as given number = (2)(another number).

Step 3: Check again if the other number that comes out is divisible by 2. If it is, keep going until the new number is no longer divisible by 2. Two things can happen here:

  • After the repeated division of 2, you end up getting a prime number. Proceed to the final step. You’re almost done!
  • After the repeated division of 2, you end up having a composite number (not prime) but cannot be divided by 2. Move to Step 4.

Step 4: Move to the next larger prime numbers such as 3, 5, 7, and so on, as needed to check if the number that we left off in the prior step can be divided evenly further. This repetitive process of dividing by prime numbers in increasing order will ultimately give us the last prime factor.

Final Step: At this point, we should have a long list of prime numbers that are being multiplied together. We just need to present our final answer as a product of exponential expressions with prime bases. That is it!  A quick example may look like this…

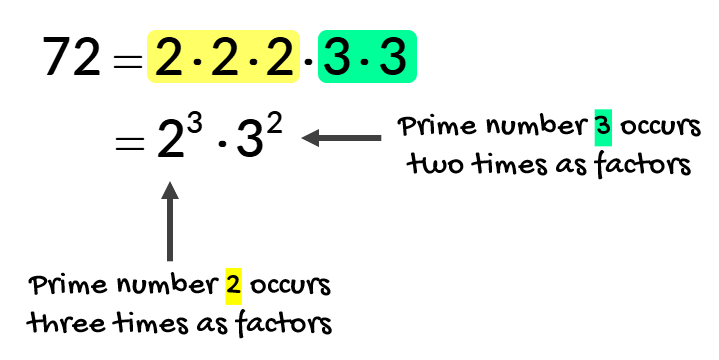
the prime factorization of 72 is equal to 2 times 2 times 2 times 3 times 3. since the prime number 2 occurs three times and the prime number 3 occurs two times as factors, we can write the factors 2 and 3 in exponential form which are 2^3 and 3^2, respectively. we can also write this as, 72 = 2×2×2×3×3 = (2^3) × (3^2).

The exponent of each prime number tells how many times that prime occurs as factors.

Examples of How to Perform Prime Factorization using Prime Factor Tree and Upside-Down Division

Example 1: Find the prime factorization of 40 and express it in exponential notation.

I begin by listing the first few prime numbers in increasing order. The goal is to keep dividing the given number by an appropriate prime number starting from the lowest until the last quotient becomes prime as well.

the first eight prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, ...

There are two common ways to perform prime factorization. The first is called the Prime Factor Tree, and the second is known as the Upside-Down Division. With this, I will also show you two ways to prime factorize the number 40.

Prime Factor Tree

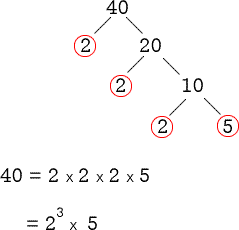
to find the prime factorization of the number 40 using the factor tree method, we divide 40 by 2 which gives us the factors 2 and 20. however, since 20 is also divisible by 2, we divide it again by 2 and get 2 and 10 as our new factors. but since 10 can still be divided by 2, we'll proceed further with one more division step getting 2 and 5 as factors. since 5 which is our last quotient is a prime number, we stop here. in summary, 40 = 2×2×2×5 = (2^3)×5.
  • Start by dividing the given number by the smallest prime which is 2.
  • The factors of the number above are broken down into “branches” as indicated by the line segments.
  • We can divide 40 and its quotient by the prime number 2 three times which means this prime number will have an exponent of 3 in the factorization.
  • The last quotient after the repeated division of 2 is a prime number which is 5.
  • Upon reaching a prime number as its last quotient in the process, this shows that we are done!

Upside-Down Division

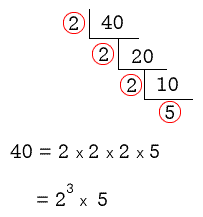
to find the prime factorization of 40 using the upside-down division method, we start by dividing 40 by 2 which gives us a quotient of 20. when using this method, we write our quotient inside the upside-down division symbol and the other factor on the left of our symbol. so for 40, our factors are 2 and 20. we write 20 inside the upside-down symbol and 2 outside the symbol, specifically to the left of the vertical bar. moving forward, if the quotient we get is divisible by 2, we keep dividing it by 2 until we get a quotient or factor that is a prime number. you will eventually notice that the solution will look like stairs. thus we have, 40=(2)(2)(2)(5) = (2^3)(5).
  • Now you know why it is called the Upside-Down Division because the division symbol is literally upside-down.
upside-down division symbol
  • I start dividing the given number by the smallest prime number which is 2. If that prime evenly divides the number, then I place the quotient below. Continue the process as needed.
  • Notice that we can perform repeated division of prime number 2, until reaching the prime number 5 as its final whole number quotient (most bottom).
  • Present the final factorization as a product of exponential numbers having a prime number base in the exponential notation.

Example 2: Find the prime factorization of 32 and express it in exponential notation.

This is an even number, and thus divisible by prime number 2. So without hesitation, I begin using it as the starting divisor of choice.

Prime Factor Tree

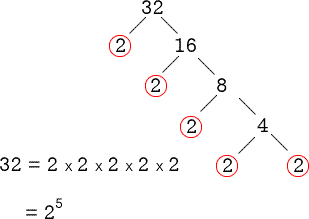
using the prime factor tree method we find the prime factorization of 32 by dividing it by 2 which gives us 16. since 16 is also divisible by 2, we divide it also by 2, giving us 2 and 8 as our new factors. we learned that we keep dividing if our quotients are divisible by 2 until we get a quotient that is a prime number. so for this case, we divide 8 again by 2, then 4 by 2. at the end, we get 2 and 2 as our last factors. 2 is a prime number so we stop here. in summary, we have 32 = (2)(2)(2)(2)(2) = 2^5.
  • Start by dividing the given number by the smallest prime which is 2.
  • The factors of the number above are broken down into “branches” as indicated by the line segments.
  • After the repeated division of 2, we also arrive at the final factor of 2. This is done!
  • Since prime number 2 appears five times as factors, then the final answer will be [latex]32 = {2^5}[/latex].

Upside-Down Division

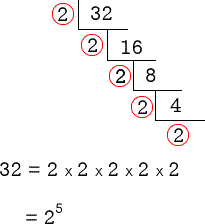
we start with 32 which is divisible by 2. just like the prime factor tree method, the upside-down division method wants us to keep dividing our quotients if they are divisible by 2 until we get a prime number. so from 32, we get the factors 2 and 16. we then divide 16 by 2 which gives us the factors 8 and 2. we proceed by dividing 8 by 2, getting 4 and 2 as factors. lastly, we will divide 4 by 2 which will give us 2 and 2 as our last factors. the prime factorization of 32 can then be written as 32 = 2×2×2×2×2 = 2^5.
  • I start dividing the given number by the smallest prime number which is 2. If that prime evenly divides the number, then I place the quotient below. Continue the process as needed.
  • This is great! We only used a single prime number to work this out until the end.
  • Prime number 2 appears five times as factors. Thus our answer is simply [latex]32 = {2^5}[/latex].

Example 3: Find the prime factorization of 147 and express it in exponential notation.

I first recognize that 147 is an odd number, therefore, not divisible by 2. Move on to the next larger prime number, which is 3.

two, three, five, seven, eleven, thirteen, seventeen, and nineteen are the first few numbers that are considered prime numbers.

I am not sure if you have encountered the “nice” divisibility rule for number 3. It states that if the sum of the digits of a number is divisible by 3, then the original number is also divisible by 3.

We have 147, the sum of its digits is 147 = 1 + 4 + 7 = 12 which is divisible by 3. This implies that 147 must also be divisible by 3.

You don’t have to show every time the prime factorization of a number using the two methods. Just pick the one that is easy or convenient for you. For this exercise, I will utilize the Factor Tree method.

Prime Factor Tree

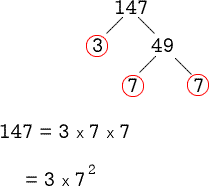
since 147 is not divisible by 2, we will start by dividing 147 by 3 which gives us 49 as the quotient. thus we have 3 and 49 as the first two factors. our next factors are 7 and 7 because 49 is not divisible by the prime numbers 2, 3, and 5. since 7 is a prime number, we stop here. in summary, 147 = (3)(7)(7) = 3(7^2).
  • Since prime number 2 can’t evenly divide 147, check on the next larger prime which is 3. Yep! This should work.
  • After dividing 147 by 3, I get 49 which is obviously a perfect square since [latex]49 = {7^2}[/latex]
  • The next logical prime number to use as the divisor is 7.

Example 4: Find the prime factorization of 540 and express it in exponential notation.

We know that any even number is always divisible by 2. So I would start dividing 540 by prime number 2. Let me use Upside-Down Division to prime factorize this number.

Upside-Down Division

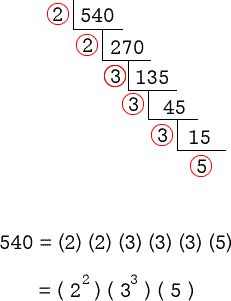
using the upside-down division, we get 540=2×2×3×3×3×5=(2^2)×(3^3)×5.
  • The given number 540 is even so 2 can divide it. Here, we perform two successive division using prime number 2 as the divisor.
  • We arrive at 135 as the partial factor which is divisible by the next larger prime, that is 3!
  • Do repeated division by 3, and you should end up with the last factor of 5 which is a prime number. That’s it! Just collect the distinct primes and assign appropriate powers or exponents to present your final answer.

Example 5: Find the prime factorization of 945 and express it in exponential notation.

You may also do the prime factorization in its most straightforward way – that is, factor out the number horizontally and down the line. Just make sure that you always start with the lowest prime number, and go to the next larger one as needed to break it down until you end up with the final prime factor. Some textbooks do it this way to save space. It’s nice to add this method to your math “toolbox”.

Solution:

2 doesn't work so we start with 3, 945=(3)(315). here, 315 is also divisible by 3. so, 945=(3)(3)(105). moving on, 105 is again divisible by 3, thus, 945=(3)(3)(3)(35). now we have 35 which is divisible by 5, so we proceed with 945=(3)(3)(3)(5)(7). by doing so, we obtain 7 which is a prime number. organizing our answer using exponential notation, we have 945=(3^3)(5)(7).

It has five prime factors where three (3) of them are distinct, namely: 3, 5, and 7.

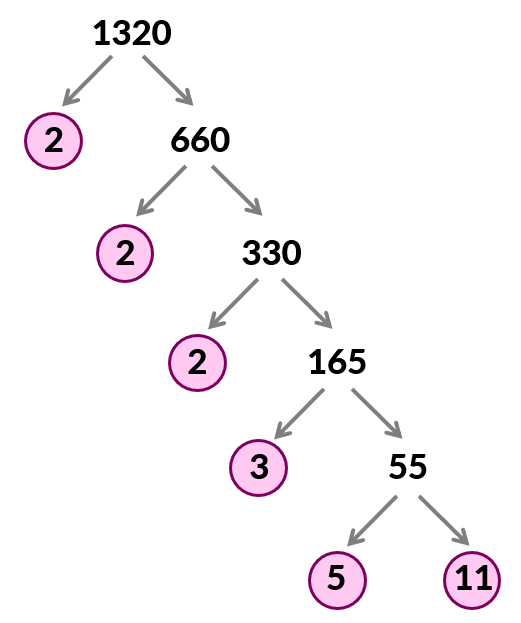
Example 6: Find the prime factorization of 1320 and express it in exponential notation.

Solution:

1320÷2=660 → 660÷2= 330 → 330÷2= 165 → 165÷3= 55 → 55÷5= 11. we will stop here because 11 is a prime number.
1320 = (2)(2)(2)(3)(5)(11) = (2^3)(3)(5)(11)

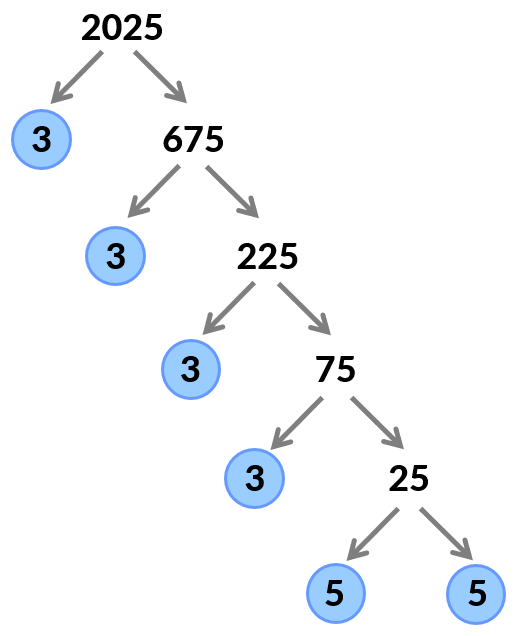
Example 7: Find the prime factorization of 2025 and express it in exponential notation.

HINT: The given number is odd, so prime number 2 cannot divide it evenly. Start with 3.

Solution:

2025÷3=675 → 675÷3=225 → 225÷3=75 → 75÷3=25 → 25÷5=5. our last two factors are 5 and 5 which is a prime number.
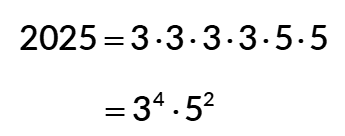
2025=(3)(3)(3)(3)(5)(5). to make our answer compact, we can write the factors in exponential form. so we have 2025=(3^4)(5^2).

Example 8: Find the prime factorization of 432 and express it in exponential notation.

NOTE: I used a slightly different method here. I call it, “Composite stays inside, Prime stays outside“. I am pertaining to the parenthesis in reference to where the composite or prime number stays.

Solution:

The goal is to keep the factored prime numbers outside the parenthesis while forcing the composite numbers to stay inside. In the end, we should have all primes and the parentheses disappear!

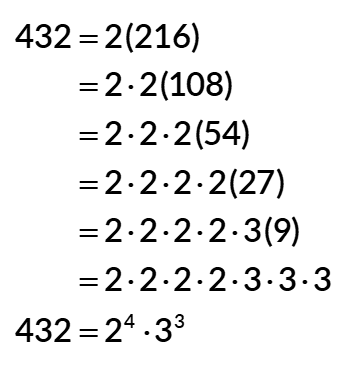
432 = 2 (216) = 2×2(108) = 2×2×2(54) = 2×2×2×2(27) = 2×2×2×2×3(9) = 2×2×2×2×3×3×3 = (2^4)×(3^3).

You might be interested in:

Fundamental Theorem of Arithmetic

List of Prime Factorizations of Integers from 2 to 200

List of Prime Factorizations of Integers from 201 to 400

List of Prime Factorizations of Integers from 401 to 600

List of Prime Factorizations of Integers from 601 to 800