Finding the Inverse Function of a Quadratic Function
What we want here is to find the inverse function – which implies that the inverse MUST be a function itself. Otherwise, we got an inverse that is not a function.
Not all functions are naturally “lucky” to have inverse functions. This happens in the case of quadratics because they all fail the Horizontal Line Test. However, if I restrict their domain to where the [latex]x[/latex] values produce a graph that would pass the horizontal line test, then I will have an inverse function.
But first, let’s talk about the test which guarantees that the inverse is a function.
Horizontal Line Test
Given a function [latex]f(x)[/latex], it has an inverse denoted by the symbol [latex]\color{red}{f^{ – 1}}\left( x \right)[/latex], if no horizontal line intersects its graph more than one time.
- Example of a graph with an inverse
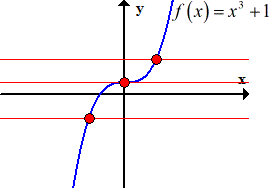
- Example of a graph without an inverse
The following are the main strategies to algebraically solve for the inverse function.
Key Steps in Finding the Inverse Function of a Quadratic Function
- Replace [latex]f(x)[/latex] by [latex]y[/latex].
- Switch the roles of [latex]\color{red}x[/latex] and [latex]\color{blue}y[/latex]. In other words, interchange [latex]x[/latex] and [latex]y[/latex] in the equation.
- Solve for [latex]y[/latex] in terms of [latex]x[/latex].
- Replace [latex]y[/latex] by [latex]{f^{ – 1}}\left( x \right)[/latex] to get the inverse function
- Sometimes, it is helpful to use the domain and range of the original function to identify the correct inverse function out of two possibilities. This happens when you get a “plus or minus” case in the end.
Examples of How to Find the Inverse Function of a Quadratic Function
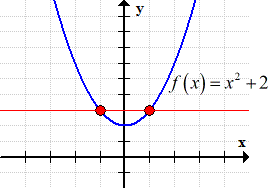
Example 1: Find the inverse function of [latex]f\left( x \right) = {x^2} + 2[/latex], if it exists. State its domain and range.
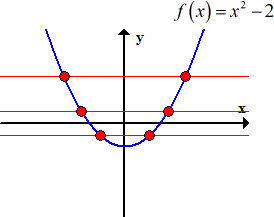
The first thing I realize is that this quadratic function doesn’t have a restriction on its domain. I am sure that when I graph this, I can draw a horizontal line that will intersect it more than once. Therefore the inverse is not a function. I will not even bother applying the key steps above to find its inverse.
The diagram shows that it fails the Horizontal Line Test, thus the inverse is not a function. I will stop here.
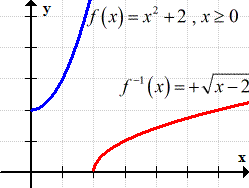
Example 2: Find the inverse function of [latex]f\left( x \right) = {x^2} + 2,\,\,x \ge 0[/latex], if it exists. State its domain and range.
This same quadratic function, as seen in Example 1, has a restriction on its domain which is [latex]x \ge 0[/latex]. After plotting the function in [latex]xy-[/latex]axis, I can see that the graph is a parabola cut in half for all [latex]x[/latex] values equal to or greater than zero. This should pass the Horizontal Line Test which tells me that I can actually find its inverse function by following the suggested steps.
In its graph below, I clearly defined the domain and range because I will need this information to help me identify the correct inverse function in the end.
Remember that the domain and range of the inverse function come from the range, and domain of the original function, respectively. It’s called the swapping of domain and range.
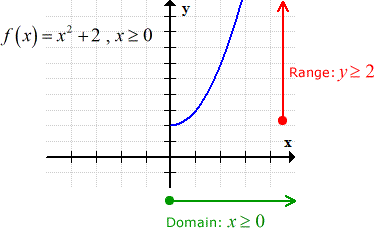
Even without solving for the inverse function just yet, I can easily identify its domain and range using the information from the graph of the original function: domain is x ≥ 2 and range is y ≥ 0.
Do you see how I interchange the domain and range of the original function to get the domain and range of its inverse?
Now, let’s go ahead and algebraically solve for its inverse.

Graphing the original function with its inverse in the same coordinate axis…
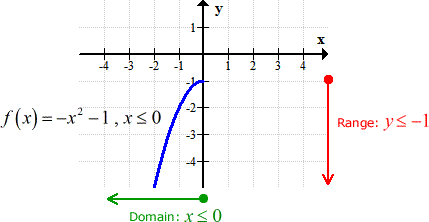
Example 3: Find the inverse function of [latex]f\left( x \right) = – {x^2} – 1,\,\,x \le 0[/latex] , if it exists. State its domain and range.
This problem is very similar to Example 2. The range starts at [latex]\color{red}y=-1[/latex], and it can go down as low as possible.
Now, these are the steps on how to solve for the inverse.
Applying square root operation results in getting two equations because of the positive and negative cases. To pick the correct inverse function out of the two, I suggest that you find the domain and range of each possible answer. Now, the correct inverse function should have a domain coming from the range of the original function; and a range coming from the domain of the same function.
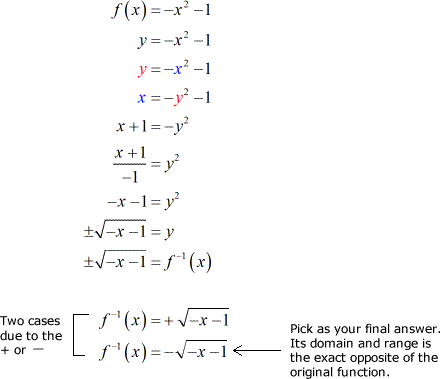
The following are the graphs of the original function and its inverse on the same coordinate axis.
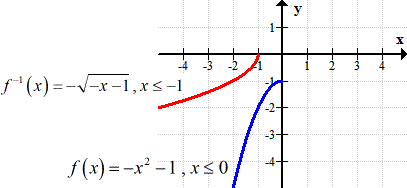
Example 4: Find the inverse of the function below, if it exists. State its domain and range.
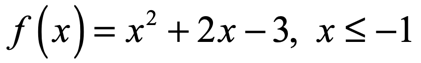
I would graph this function first and clearly identify the domain and range. Notice that the restriction in the domain cuts the parabola into two equal halves. I will deal with the left half of this parabola. Clearly, this has an inverse function because it passes the Horizontal Line Test.
Proceed with the steps in solving for the inverse function. In fact, there are two ways how to work this out.
- Solve this by the Quadratic Formula as shown below.
[latex]x = {\Large{{{ – b \pm \sqrt {{b^2} – 4ac} } \over {2a}}}}[/latex]
where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] can contain variables.
This is expected since we are solving for a function, not exact values.
The key step here is to pick the appropriate inverse function in the end because we will have the plus (+) and minus (−) cases. We can do that by finding the domain and range of each and compare that to the domain and range of the original function. Remember that we swap the domain and range of the original function to get the domain and range of its inverse.
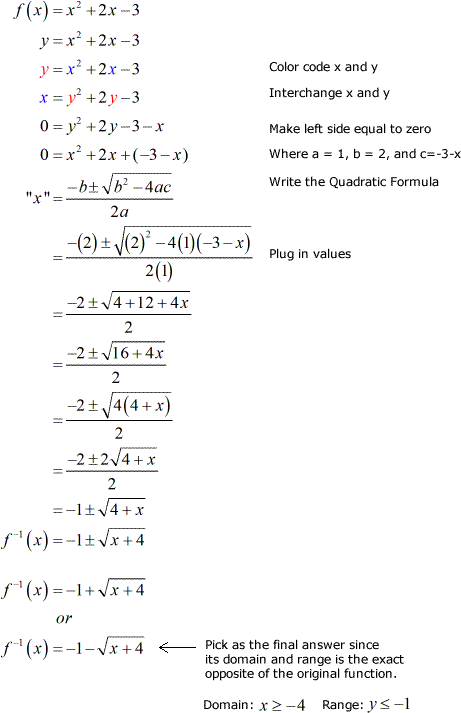
- The method of completing the squares allows us to isolate the variable in a quadratic trinomial. As you will see in the steps, the quadratic trinomial is converted into a linear binomial raised to the power of [latex]2[/latex]. Obviously, we can apply the square root operation to get rid of the exponent [latex]2[/latex], therefore leaving us with an easy equation to solve.

If you observe, the graphs of the function and its inverse are actually symmetrical along the line [latex]y = x[/latex] (see dashed line). They are like mirror images of each other.
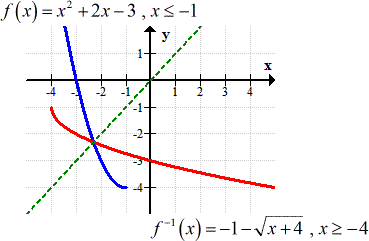
I hope that you gain some level of appreciation for how to find the inverse of a quadratic function. Although it can be a bit tedious, as you can see, overall it is not that bad. I recommend that you check out the related lessons on how to find inverses of other kinds of functions.
You may also be interested in these related math lessons or tutorials:
Inverse of Absolute Value Function
Inverse of Exponential Function
