What is the Horizontal Line Test?

The horizontal line test is a convenient method that can determine if the inverse of a function is also a function.

It is possible that the inverse of a function is not a function because it doesn’t pass the vertical line test.

So here’s the deal!

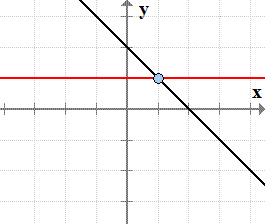
If the horizontal line intersects the graph of a function in all places at exactly one point, then the given function has an inverse that is also a function. We say this function passes the horizontal line test.

Here are some examples of functions that pass the horizontal line test:

Horizontal Line Cutting or Hitting the Graph at Exactly One Point

  • Graph of the line [latex]f\left( x \right) = – x + 2[/latex].
the graph of the line f(x)=-x+2 is cut by a horizontal at exactly one point
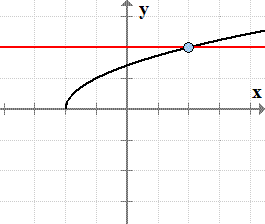
  • Graph of the square root function [latex]f\left( x \right) = \sqrt {x + 1}[/latex]

the graph of an square root function f(x)=sqrt(x=1) is cut by a horizontal line at exactly one point.
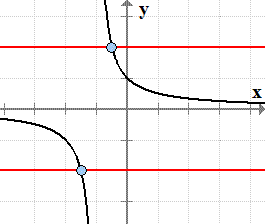
  • Graph of the rational function [latex]\large{f\left( x \right) = {1 \over {x + 1}}}[/latex].

the graph of a rational function f(x)=1/(x+1) is cut by the horizontal line at exactly one point

On the other hand, if the horizontal line can intersect the graph of a function in some places at more than one point, then the function involved can’t have an inverse that is also a function.

We say this function fails the horizontal line test.

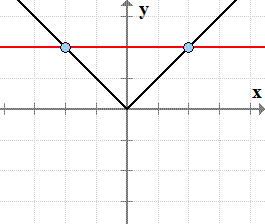
Here are some examples of functions that fail the horizontal line test:

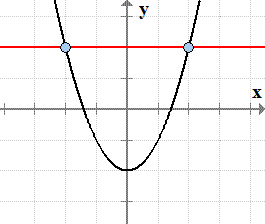
Horizontal Line Cutting or Hitting the Graph at More Than One Point

  • Graph of the parabola [latex]f\left( x \right) = {x^2} – 2[/latex].
the graph of a quadratic function is cut by horizontal line in exactly two points
  • Graph of absolute value function [latex]f\left( x \right) = \left| x \right|[/latex]

the graph of the absolute value function is cut by a horizontal line at two points
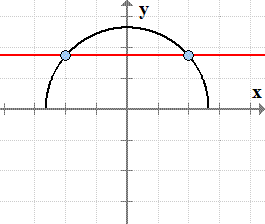
  • Graph of semi-circle [latex]f\left( x \right) = \sqrt {7 – {x^2}}[/latex]

the graph of a semi-circle is cut by a horizontal line at exactly two points

You may also be interested in these related math lessons or tutorials:

Vertical Line Test