Vertical Line Test
The vertical line test is a method that is used to determine whether a given relation is a function or not. The approach is rather simple. Draw a vertical line cutting through the graph of a relation, and then observe the points of intersections.
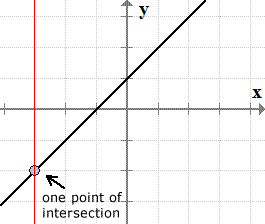
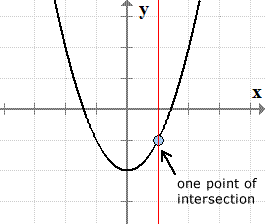
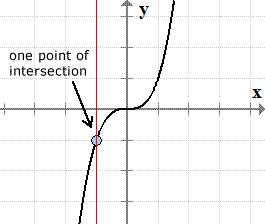
The vertical line test supports the definition of a function. That is, every [latex]x[/latex]-value of a function must be paired to a single [latex]y[/latex]-value. If a vertical line intersects the graph of a relation at exactly one point, it implies that a single [latex]x[/latex]-value is only paired to a unique value of [latex]y[/latex].
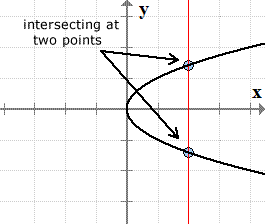
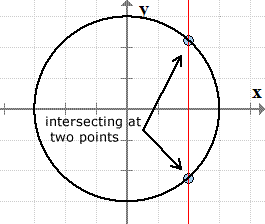
On the other hand, if the vertical line intersects the graph more than once, this suggests that a single [latex]x[/latex]-value is being associated with more than one value of [latex]y[/latex]. This condition causes the relation to be “disqualified” as a function.
So here’s the deal!
If a vertical line intersects the graph in all places at exactly one point, then the relation is a function.
If a vertical line intersects the graph in some places more than once, then the relation is NOT a function.
Here are some examples of relations that are also functions because they pass the vertical line test.
Cutting or Hitting the Graph at Exactly One Point
Graph of the line [latex]f\left( x \right) = x + 1[/latex]
Graph of the quadratic function (parabola) [latex]f\left( x \right) = {x^2} – 2[/latex]
Graph of the cubic function [latex]f\left( x \right) = {x^3}[/latex]
If a vertical line intersects the graph in some places at more than one point, then the relation is NOT a function.
Here are some examples of relations that are NOT functions because they fail the vertical line test.
Cutting or Hitting the Graph in More Than One Point
Graph of the “sideway” parabola [latex]x = {y^2}[/latex]
Graph of the circle [latex]{x^2} + {y^2} = 9[/latex]
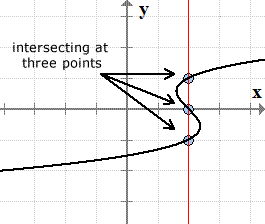
Graph of the relation [latex]x = {y^3} – y + 2[/latex]
You might also be interested in: