How to Solve Quadratic Equations using the Completing the Square Method
If you are already familiar with the steps involved in completing the square, you may skip the introductory discussion and review the seven (7) worked examples right away.
The key step in this method is to find the constant “[latex]k[/latex]” that will allow us to express the given trinomial as the square of a binomial.
For instance,
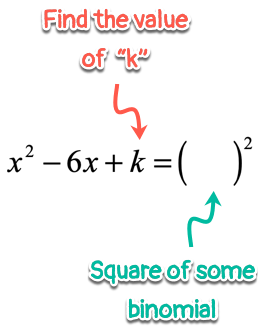
The value of “[latex]k[/latex]” is determined by squaring one-half of the coefficient of [latex]x[/latex]. In this case, the coefficient of the linear term [latex]x[/latex] is [latex] – \,6[/latex].
Therefore, half of [latex] – \,6[/latex] is [latex] – \,3[/latex], and its square [latex]{\left( { – \,3} \right)^2} = 9[/latex]. The value of [latex]k[/latex] must be [latex]9[/latex]!
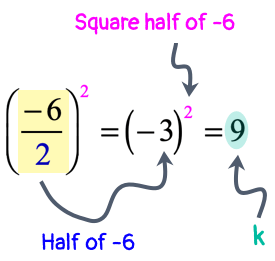
If I substitute [latex]k[/latex] by [latex]9[/latex], the trinomial is factored into two equal binomials. This is great because I can now rewrite it in a more compact form, that is, the square of a single binomial.
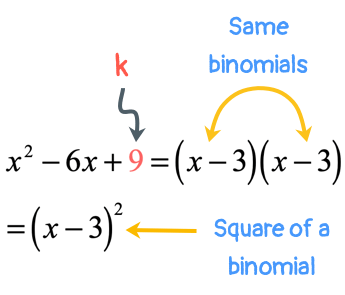
The following are the general steps involved in solving quadratic equations using completing the square method.
Key Steps in Solving Quadratic Equation by Completing the Square
1) Keep all the [latex]x[/latex]-terms (both the squared and linear) on the left side, while moving the constant to the right side.
In symbol, rewrite the general form [latex]a{x^2} + bx + c[/latex] as:
[latex]a{x^2} + bx = – \,c[/latex]
2) Now, identify what type of problem you have by looking at the coefficient of the leading term, [latex]a[/latex].
Examples:
- “Easy Type” when [latex]a = 1[/latex]
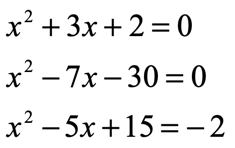
- “Difficult Type” when [latex]a \ne 1[/latex]
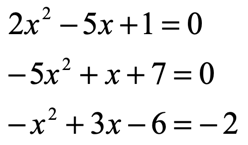
3) If you have the “Easy type”, proceed immediately to Step 4. If you have the “Difficult Type”, you must divide the entire equation first by the value of [latex]a[/latex] before moving to step 4.
4) Take the coefficient of [latex]x[/latex]-term, divide it by [latex]2[/latex] then square its result. Add this value to both sides of the equation.
5) Express the left side as a square of binomial.
6) Get the square root of both sides of the equation. Don’t forget to attach the [latex] \pm [/latex] symbol on the right side!
7) Finish it off by solving the linear equation(s) that arise from it.
Examples of How to Solve Quadratic Equations by Completing the Square
Example 1: Solve the quadratic equation below by completing the square method.
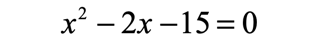
This is an “Easy Type” since [latex]a = 1[/latex]. I will keep the “[latex]x[/latex]-terms” (both the squared and linear terms) on the left side but move the constant to the right side.
I can do that by adding [latex]15[/latex] on both sides of the equation.
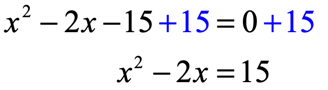
Now, take the coefficient of the linear term (which is the [latex]x[/latex]-term with power [latex]1[/latex]) and perform TWO operations on it:
- Divide by [latex]2[/latex], followed by
- Squaring (raising to the 2nd power)
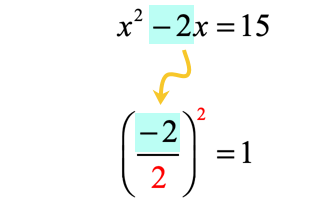
The output here, which is [latex]+1[/latex], will be added to both sides of the quadratic equation.
This step forces the left side to generate a perfect-square-trinomial which can be expressed as a square of a binomial. Great!
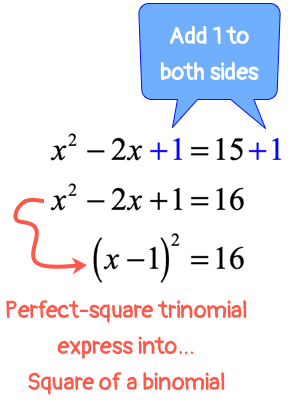
At this point, it is very easy to solve for [latex]x[/latex]. To get rid of the exponent [latex]2[/latex] in the binomial, I will apply square root operation on both sides of the equation.
Next, solve the pair of linear equations that arise as a result of squaring both sides.
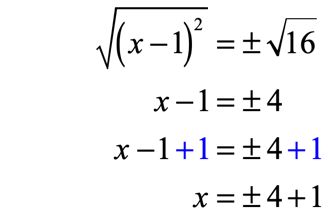
Break [latex]x = \pm \,4 + 1[/latex] into two cases, then solve.
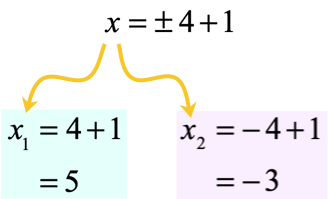
That is it! Our answers are [latex]{x_1} = 5[/latex] and [latex]{x_2} = – \,3[/latex].
Make it a habit to check your solved values of [latex]x[/latex] back into the original equation to verify if indeed they are “true” answers. I will leave it to you as an exercise.
Example 2: Solve the quadratic equation below by completing the square method.
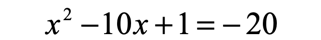
Obviously, I can’t proceed with the steps required in completing the square. I must isolate the [latex]x[/latex]-terms to the left, and the constant to the right.
Do that by subtracting both sides by [latex]1[/latex].
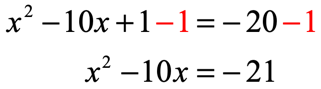
This time I am ready to perform the completing the square steps to solve this quadratic equation. Start by taking the coefficient of the linear [latex]x[/latex]-term then divide it by [latex]2[/latex] followed by squaring it. This is the MOST important step of this whole process.
Whatever number that comes out will be added to both sides of the equation. The left side becomes a perfect square trinomial which can be rewritten as the square of binomial.
Eliminate the power [latex]2[/latex] of the binomial by taking the square root of both sides. I hope that you’ll be able to follow the rest of the solution.
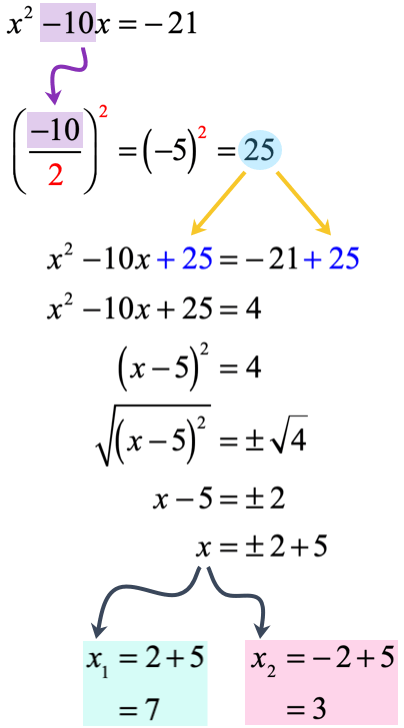
I got the following as the answers which are [latex]{x_1} = 7[/latex] and [latex]{x_2} = 3[/latex]. Go ahead and check the solutions yourself as an exercise.
Example 3: Solve the quadratic equation below by completing the square method.
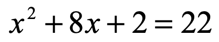
Solution:
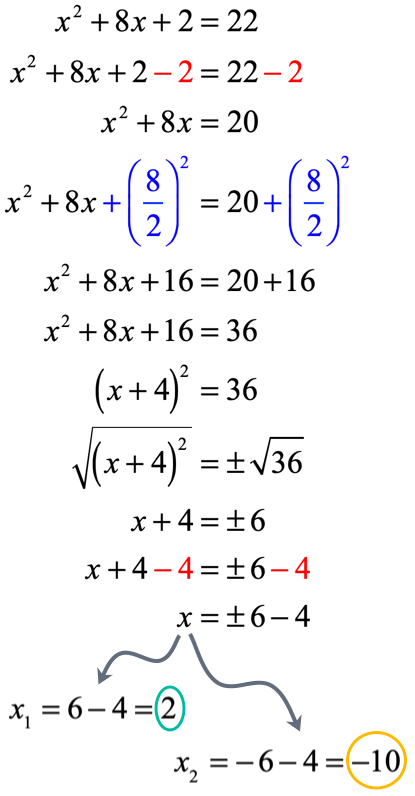
The answers are [latex]{x_1} = 2[/latex] and [latex]{x_2} = – 10[/latex]
Example 4: Solve the quadratic equation below by completing the square method.
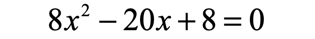
The first thing to do is to move the constant to the right side by subtracting each side by [latex]8[/latex].
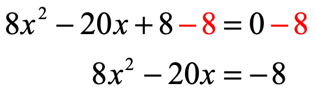
This is actually the “Difficult Type” since [latex]a \ne 1[/latex]. Thus, I need to make the coefficient of the squared [latex]x[/latex]-term equal to [latex]1[/latex]. This can be done by dividing through the entire equation by [latex]a[/latex] which equals [latex]8[/latex]!
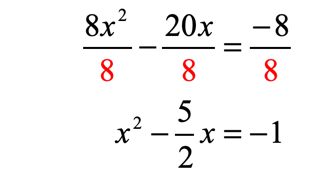
By dividing through by [latex]8[/latex], I have converted this problem into the “easy” case because the coefficient of the squared [latex]x[/latex]-term becomes [latex]+1[/latex]. Finish this off by doing the same process as seen in examples 1 and 2. The only difference is that I will deal with fractions.
Consider the coefficient of the linear [latex]x[/latex]-term, divide by [latex]2[/latex] and square it.
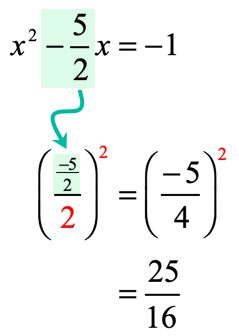
Take the output of the step above, and add to both sides of the quadratic equation. Then proceed with the rest of the steps to complete the square.
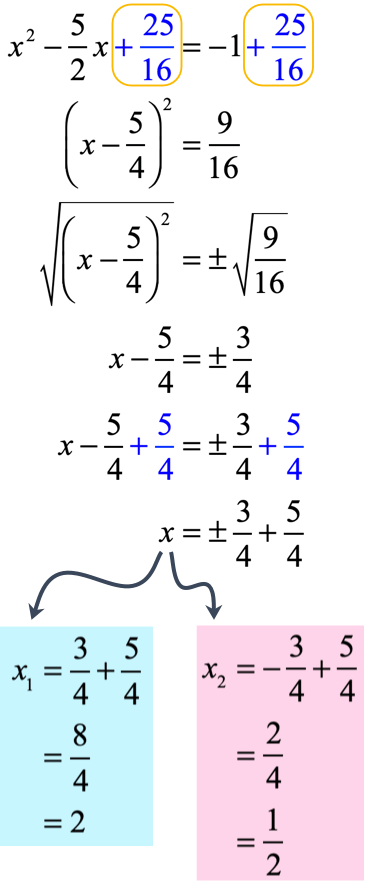
The answers should be [latex]{x_1} = 2[/latex] and [latex]{x_2} = {1 \over 2}[/latex].
Example 5 (Practice Problem): Solve the quadratic equation below by completing the square method.
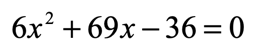
Try solving this problem on your own first. Then click below to view the solution.
Answer
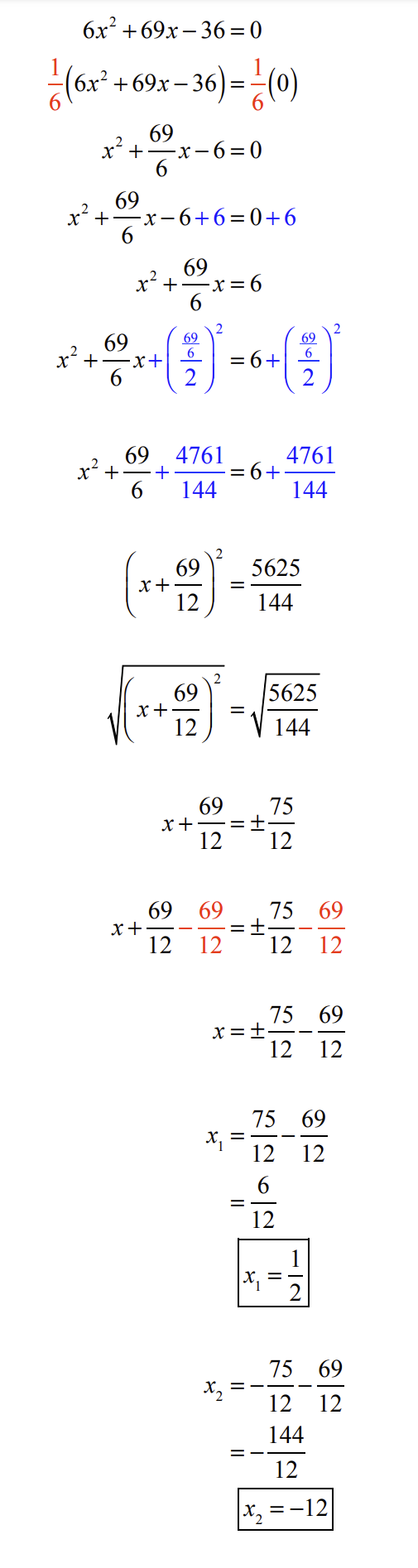
NOTE: The solution to this problem may look messy but as long as you apply the correct procedures for completing the square, you will soon realize that the answers to this problem come out nicely.
Hint: The solution set includes a rational number and a negative integer.
Example 6: Solve the quadratic equation below by completing the square method.
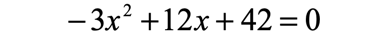
I will move the constant to the right side while keeping all [latex]x[/latex]-terms on the left. Then I must divide the entire equation by [latex] – \,3[/latex] since [latex]a \ne 1[/latex].
- Subtract both sides by [latex]42[/latex]
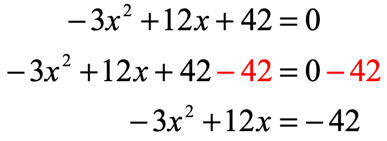
- Divide entire equation by [latex] – \,3[/latex]
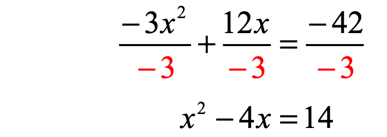
Now, I will take the coefficient of the linear term, divide it by [latex]2[/latex] and square it.
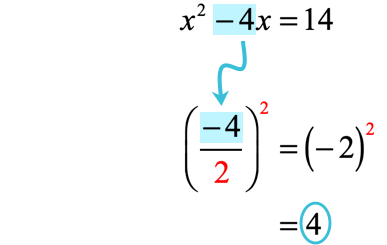
Add this output [latex]4[/latex] to both sides of the equation. This makes the left side a perfect-square-trinomial which can be rewritten as the square of a binomial.

That was easy, right? Again, the more you see how these problems are being solved correctly, the better you become!
Example 7 (Practice Problem): Solve the quadratic equation below using the completing the square method.
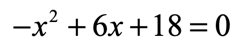
Try solving this problem on your own first. Then click below to view the solution.
Answer
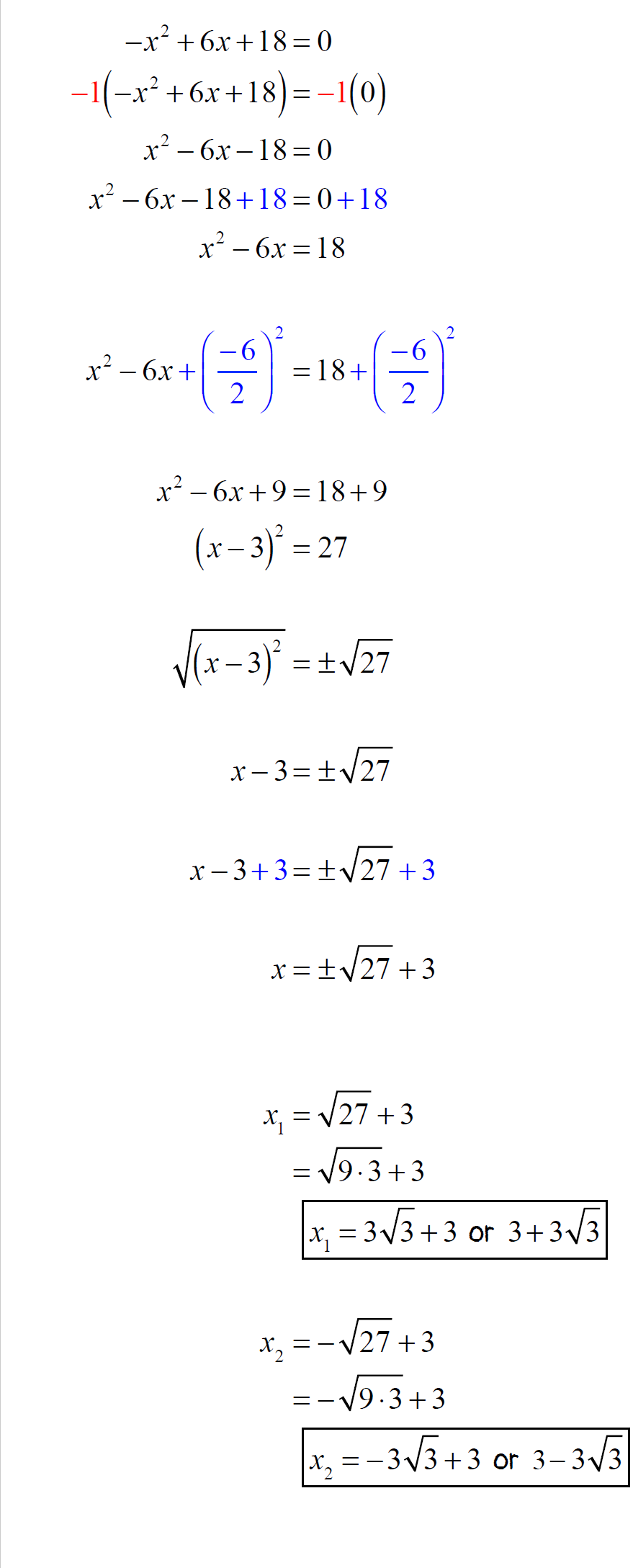
You may also be interested in these related math lessons or tutorials:
Solving Quadratic Equations by Square Root Method
Solving Quadratic Equations by Factoring Method
Solving Quadratic Equations by the Quadratic Formula
