How to Solve Quadratic Equations using the Quadratic Formula
There are times when we are stuck solving a quadratic equation of the form [latex]a{x^2} + bx + c = 0[/latex] because the trinomial on the left side can’t be factored out easily. It doesn’t mean that the quadratic equation has no solution. At this point, we need to call upon the straightforward approach of the quadratic formula to find the solutions of the quadratic equation or put simply, determine the values of [latex]x[/latex] that can satisfy the equation.
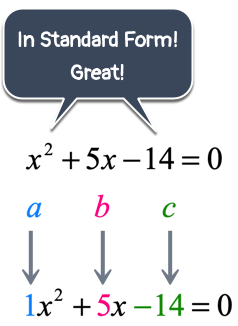
In order use the quadratic formula, the quadratic equation that we are solving must be converted into the “standard form”, otherwise, all subsequent steps will not work. The goal is to transform the quadratic equation such that the quadratic expression is isolated on one side of the equation while the opposite side only contains the number zero, [latex]0[/latex].
Take a look at the diagram below.
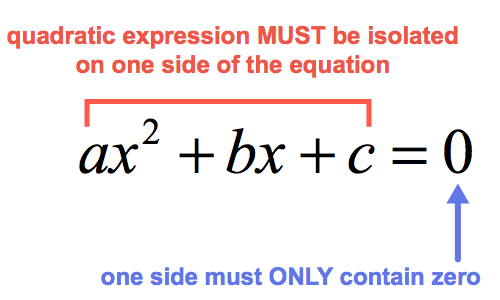
In this convenient format, the numerical values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are easily identified! Upon knowing those values, we can now substitute them into the quadratic formula then solve for the values of [latex]x[/latex].
The Quadratic Formula
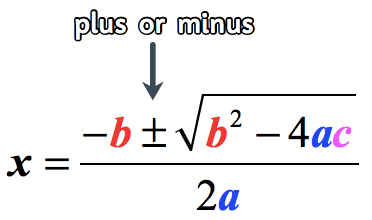
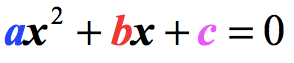
- Where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are the coefficients of an arbitrary quadratic equation in the standard form, [latex]a{x^2} + bx + c = 0[/latex].
Slow down if you need to. Be careful with every step while simplifying the expressions. This is where common mistakes usually happen because students tend to “relax” which results to errors that could have been prevented, such as in the addition, subtraction, multiplication and/or division of real numbers.
Examples of How to Solve Quadratic Equations by the Quadratic Formula
Example 1: Solve the quadratic equation below using the Quadratic Formula.
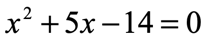
By inspection, it’s obvious that the quadratic equation is in the standard form since the right side is just zero while the rest of the terms stay on the left side. In other words, we have something like this

This is great! What we need to do is simply identify the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] then substitute into the quadratic formula.

That’s it! Make it a habit to always check the solved values of [latex]x[/latex] back into the original equation to verify.
Example 2: Solve the quadratic equation below using the Quadratic Formula.
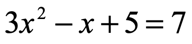
This quadratic equation is absolutely not in the form that we want because the right side is NOT zero. I need to eliminate that [latex]7[/latex] on the right side by subtracting both sides by [latex]7[/latex]. That takes care of our problem. After doing so, solve for [latex]x[/latex] as usual.
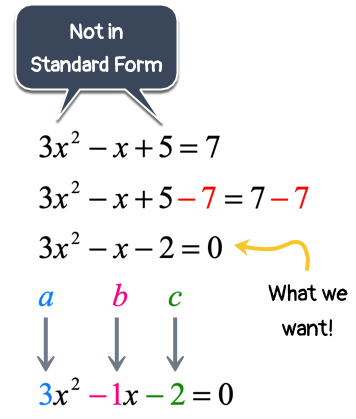
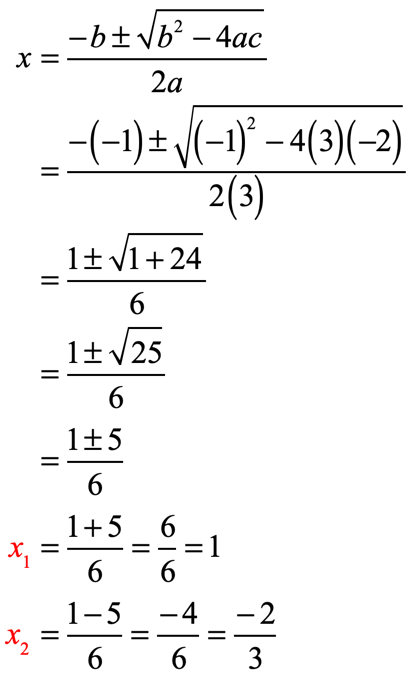
The final answers are [latex]{x_1} = 1[/latex] and [latex]{x_2} = – {2 \over 3}[/latex].
Example 3: Solve the quadratic equation below using the Quadratic Formula.
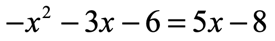
This quadratic equation looks like a “mess”. I have variable [latex]x[/latex]’s and constants on both sides of the equation. If we are faced with something like this, always stick to what we know. Yes, it’s all about the Standard Form. We have to force the right side to be equal to zero. We can do just that in two steps.
I will first subtract both sides by [latex]5x[/latex], and followed by the addition of [latex]8[/latex].

Values we need:
[latex]a = – 1[/latex], [latex]b = – \,8[/latex], and [latex]c = 2[/latex]
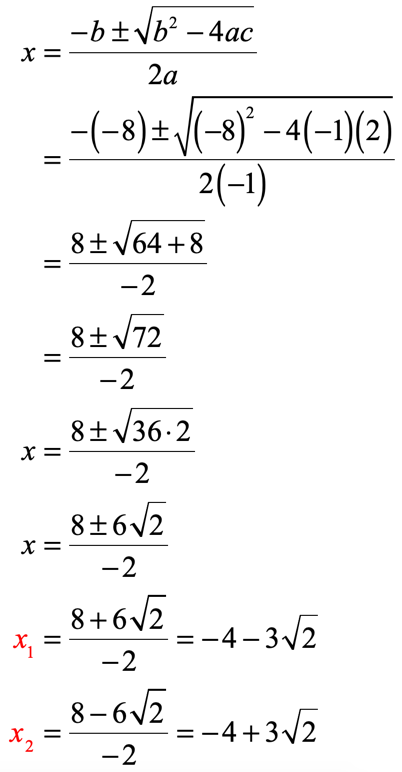
Example 4: Solve the quadratic equation below using the Quadratic Formula.
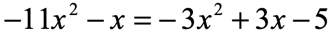
Well, if you think that Example [latex]3[/latex] is a “mess” then this must be even “messier”. However, you’ll soon realize that they are really very similar.
We first need to perform some cleanup by converting this quadratic equation into standard form. Sounds familiar? Trust me, this problem is not as bad as it looks, as long as we know what to do.
Just to remind you, we want something like this

Therefore, we must do whatever it takes to make the right side of the equation equal to zero. Since we have three terms on the right side, it follows that three steps are required to make it zero.
The solution below starts by adding both sides by [latex]3{x^2}[/latex], followed by subtraction of [latex]3x[/latex], and finally the addition of [latex]5[/latex]. Done!
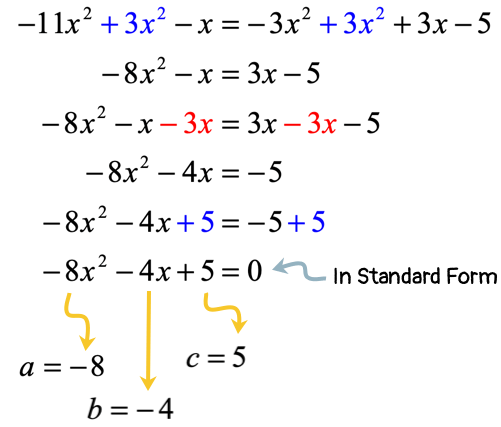
After making the right side equal to zero, the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are easy to identify. Plug those values into the quadratic formula, and simplify to get the final answers!

Example 5: Solve the quadratic equation below using the Quadratic Formula.
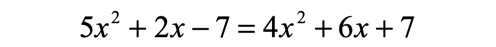
First, we need to rewrite the given quadratic equation in Standard Form, [latex]a{x^2} + bx + c = 0[/latex].
- Eliminate the [latex]{x^2}[/latex] term on the right side.
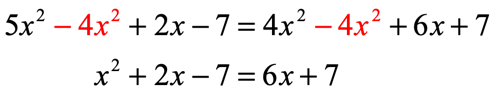
- Eliminate the [latex]x[/latex] term on the right side.
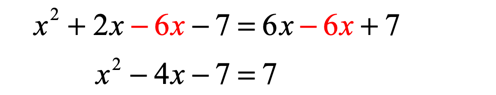
- Eliminate the constant on the right side.
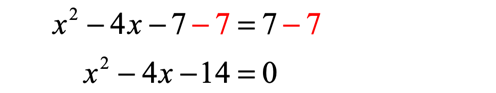
After getting the correct standard form in the previous step, it’s now time to plug the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] into the quadratic formula to solve for [latex]x[/latex].
- From the converted standard form, extract the required values.
[latex]a = 1[/latex], [latex]b = – \,4[/latex], and [latex]c = – \,14[/latex]
- Then evaluate these values into the quadratic formula.

You may also be interested in these related math lessons or tutorials:
Quadratic Formula Practice Problems with Answers
Solving Quadratic Equations by Square Root Method
Solving Quadratic Equations by Factoring Method
Solving Quadratic Equations by Completing the Square
