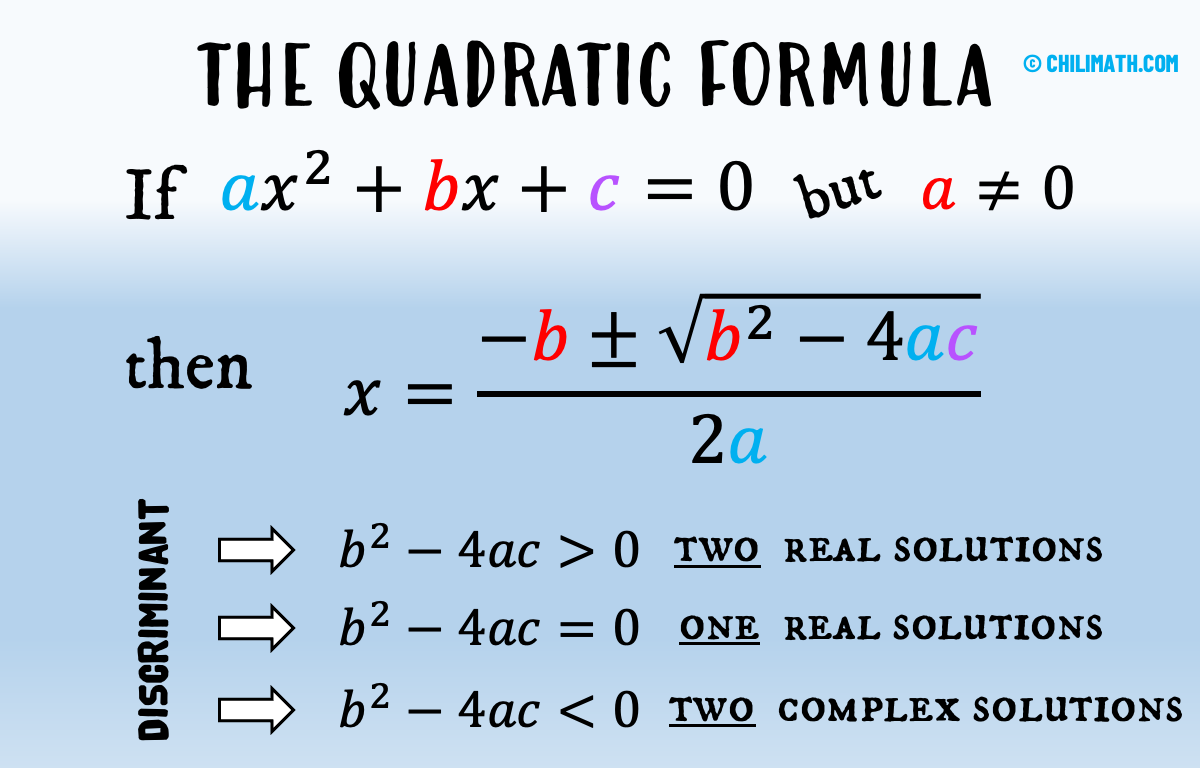Quadratic Formula Practice Problems with Answers
Below are ten (10) practice problems regarding the quadratic formula. The more you use the formula to solve quadratic equations, the more you become expert at it!
Use the illustration below as a guide. Notice that in order to apply the quadratic formula, we must transform the quadratic equation into the standard form, that is, [latex]a{x^2} + bx + c = 0[/latex] where [latex]a \ne 0[/latex].
The problems below have varying levels of difficulty. I encourage you to try them all. Believe me, they are actually easy! Good luck.
Problem 1: Solve the quadratic equation using the quadratic formula.
[latex]{x^2}\, – \,8x + 12 = 0[/latex]
Answer
\begin{align*} &a = 1 \\ &b = – 8 \\ &c = 12 \\ \\ x &= {{ – b \pm \sqrt {{b^2} – 4ac} } \over {2a}} \\ \\ &= {{ – \left( { – 8} \right) \pm \sqrt {{{\left( { – 8} \right)}^2} – 4\left( 1 \right)\left( {12} \right)} } \over {2\left( 1 \right)}} \\ \\ & = {{8 \pm \sqrt {64 – 48} } \over 2} \\ \\ & = {{8 \pm \sqrt {16} } \over 2} \\ \\ & = {{8 \pm 4} \over 2} \\ \\ {x_1} &= {{8 + 4} \over 2} \\ \\ & = {{12} \over 2} \\ \\ & = \boxed{\color{red}6} \\ \\ {x_2} &= {{8 – 4} \over 2} \\ \\ & = {4 \over 2} \\ \\ & = \boxed{\color{red}2} \end{align*}Therefore, the answers are [latex]{x_1} = 6[/latex] and [latex]{x_2} = 2[/latex].
Problem 2: Solve the quadratic equation using the quadratic formula.
[latex]2{x^2}\, -\, x = 1[/latex]
Answer
Rewrite the quadratic equation in the standard form.
[latex]2{x^2} – x – 1 = 0[/latex]
\begin{align*} & a = 2 \\ & b = – 1 \\ & c = – 1 \\ \\ x &= {{ – b \pm \sqrt {{b^2} – 4ac} } \over {2a}} \\ \\ & = {{ – \left( { – 1} \right) \pm \sqrt {{{\left( { – 1} \right)}^2} – 4\left( 2 \right)\left( { – 1} \right)} } \over {2\left( 2 \right)}} \\ \\ & = {{1 \pm \sqrt {1 + 8} } \over 4} \\ \\ & = {{1 \pm \sqrt 9 } \over 4} \\ \\ & = {{1 \pm 3} \over 4} \\ \\ {x_1} &= {{1 + 3} \over 4} \\ \\ & = {4 \over 4} \\ \\ & =\boxed{\color{red} 1} \\ \\ {x_2} &= {{1 – 3} \over 4} \\ \\ & = {{ – 2} \over 4} \\ \\ & = \boxed{\color{red}{{ – 1} \over 2}} \end{align*}Therefore, the answers are [latex]{x_1} = 1[/latex] and [latex]{x_2} = \large{{ – 1} \over 2}[/latex].
Problem 3: Solve the quadratic equation using the quadratic formula.
[latex]4{x^2} + 9 = – 12x[/latex]
Answer
Rewrite the quadratic equation in the standard form.
[latex]4{x^2} + 12x + 9 = 0[/latex]
\begin{align*} & a = 4 \\ & b = 12 \\ & c = 9 \\ \\ x &= {{ – b \pm \sqrt {{b^2} – 4ac} } \over {2a}} \\ \\ & = {{ – \left( {12} \right) \pm \sqrt {{{\left( {12} \right)}^2} – 4\left( 4 \right)\left( 9 \right)} } \over {2\left( 4 \right)}} \\ \\ & = {{ – 12 \pm \sqrt {144 – 144} } \over 8} \\ \\ & = {{ – 12 \pm \sqrt 0 } \over 8} \\ \\ & = {{ – 12} \over 8} \\ \\ x &=\boxed{\color{red} {{ – 3} \over 2}} \end{align*}Therefore, the solution is [latex]x = \large{{ – 3} \over 2}[/latex].
Problem 4: Solve the quadratic equation using the quadratic formula.
[latex]5{x^2} = 7x + 6[/latex]
Answer
Convert the quadratic equation into the standard form.
[latex]5{x^2} – 7x – 6 = 0[/latex]
\begin{align*} & a = 5 \\ & b = – 7 \\ & c = – 6 \\ \\ x &= {{ – b \pm \sqrt {{b^2} – 4ac} } \over {2a}} \\ \\ & = {{ – \left( { – 7} \right) \pm \sqrt {{{\left( { – 7} \right)}^2} – 4\left( 5 \right)\left( { – 6} \right)} } \over {2\left( 5 \right)}} \\ \\ & = {{7 \pm \sqrt {49 + 120} } \over {10}} \\ \\ & = {{7 \pm \sqrt {169} } \over {10}} \\ \\ & = {{7 \pm 13} \over {10}} \\ \\ {x_1} &= {{7 + 13} \over {10}} \\ \\ & = {{20} \over {10}} \\ \\ & =\boxed {\color{red} 2} \\ \\ {x_2} &= {{7 – 13} \over {10}} \\ \\ & = {{ – 6} \over {10}} \\ \\ & =\boxed{\color{red} {{ – 3} \over 5}} \end{align*}Therefore, the answers are [latex]{x_1} = 2[/latex] and [latex]{x_2} = \large{{ – 3} \over 5}[/latex].
Problem 5: Solve the quadratic equation using the quadratic formula.
[latex]{x^2} -\,{ \large{1 \over 2}}x\, – \,{\large{3 \over {16}}} = 0[/latex]
Answer
Multiply the entire equation by the LCM of the denominators which is [latex]16[/latex]. This will get rid of the denominators thereby giving us integer values for [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex].
[latex]16{x^2} – 8x – 3 = 0[/latex]
\begin{align*} & a = 16 \\ & b = – 8 \\ & c = – 3 \\ \\ x &= {{ – b \pm \sqrt {{b^2} – 4ac} } \over {2a}} \\ \\ & = {{ – \left( { – 8} \right) \pm \sqrt {{{\left( { – 8} \right)}^2} – 4\left( {16} \right)\left( { – 3} \right)} } \over {2\left( {16} \right)}} \\ \\ & = {{8 \pm \sqrt {64 + 192} } \over {32}} \\ \\ & = {{8 \pm \sqrt {256} } \over {32}} \\ \\ & = {{8 \pm 16} \over {32}} \\ \\ {x_1} &= {{8 + 16} \over {32}} \\ \\ & = {{24} \over {32}} \\ \\ & = \boxed{\color{red}{3 \over 4}} \\ \\ {x_2} &= {{8 – 16} \over {32}} \\ \\ & = {{ – 8} \over {32}} \\ \\ & =\boxed{\color{red} {{ – 1} \over 4}} \end{align*}Therefore, the answers are [latex]x_1=\large{3 \over 4}[/latex] and [latex]x_2=\large{{ – 1} \over 4}[/latex].
Problem 6: Solve the quadratic equation using the quadratic formula.
[latex]{x^2} + 3x + 9 = 5x – 8[/latex]
Answer
Convert into standard form as [latex]{x^2} – 2x + 17 = 0[/latex].
\begin{align*} & a = 1 \\ & b = – 2 \\ & c = 17 \\ \\ x &= {{ – b \pm \sqrt {{b^2} – 4ac} } \over {2a}} \\ \\ & = {{ – \left( { – 2} \right) \pm \sqrt {{{\left( { – 2} \right)}^2} – 4\left( 1 \right)\left( {17} \right)} } \over {2\left( 1 \right)}} \\ \\ & = {{2 \pm \sqrt {4 – 68} } \over 2} \\ \\ & = {{2 \pm \sqrt { – 64} } \over 2} \\ \\ & = {{2 \pm \sqrt {64} \cdot \sqrt { – 1} } \over 2} \\ \\ & = {{2 \pm 8 \cdot i} \over 2} \\ \\ {x_1} &= {{2 + 8 \cdot i} \over 2} \\ \\ & = {{2 + 8 \cdot i} \over 2} \\ \\ & = {2 \over 2} + {8 \over 2}i \\ \\ & = \boxed{\color{red}1 + 4i} \\ \\ {x_2} &= {{2 – 8 \cdot i} \over 2} \\ \\ & = {2 \over 2} – {8 \over 2}i \\ \\ & = \boxed {\color{red}1 – 4i } \end{align*}Therefore, the answers are [latex]x_1=1 + 4i[/latex] and [latex]x_2=1 – 4i[/latex].
Problem 7: Solve the quadratic equation using the quadratic formula.
[latex]{\left( {x – 2} \right)^2} = 4x[/latex]
Answer
Rewrite in standard form as [latex]{x^2} – 8x + 4 = 0[/latex].
\begin{align*} & a = 1 \\ & b = – 8 \\ & c = 4 \\ \\ x &= {{ – b \pm \sqrt {{b^2} – 4ac} } \over {2a}} \\ \\ & = {{ – \left( { – 8} \right) \pm \sqrt {{{\left( { – 8} \right)}^2} – 4\left( 1 \right)\left( 4 \right)} } \over {2\left( 1 \right)}} \\ \\ & = {{8 \pm \sqrt {64 – 16} } \over 2} \\ \\ & = {{8 \pm \sqrt {48} } \over 2} \\ \\ & = {{8 \pm \sqrt {16} \cdot \sqrt 3 } \over 2} \\ \\ & = {{8 \pm 4 \cdot \sqrt 3 } \over 2} \\ \\ {x_1} &= {{8 + 4 \cdot \sqrt 3 } \over 2} \\ \\ & = {8 \over 2} + {4 \over 2}\sqrt 3 \\ \\ & = \boxed {\color{red}4 + 2\sqrt 3} \\ \\ {x_2} &= {{8 – 4 \cdot \sqrt 3 } \over 2} \\ \\ & = {8 \over 2} – {4 \over 2}\sqrt 3 \\ \\ & = \boxed {\color{red}4 – 2\sqrt 3} \end{align*}Hence, the answers are [latex]{x_1} = 4 + 2\sqrt 3 [/latex] and [latex]{x_2} = 4 – 2\sqrt 3 [/latex].
Problem 8: Solve the quadratic equation using the quadratic formula.
[latex]{\Large{{{x^2}} \over 4} – {x \over 2} }= 1[/latex]
Answer
To convert the quadratic equation into the standard form, simply multiply the entire equation by [latex]4[/latex] then subtract both sides by [latex]4[/latex].
[latex]{x^2} – 2x – 4 = 0[/latex]
\begin{align*} & a = 1 \\ & b = – 2 \\ & c = – 4 \\ \\ x &= {{ – b \pm \sqrt {{b^2} – 4ac} } \over {2a}} \\ \\ & = {{ – \left( { – 2} \right) \pm \sqrt {{{\left( { – 2} \right)}^2} – 4\left( 1 \right)\left( { – 4} \right)} } \over {2\left( 1 \right)}} \\ \\ & = {{2 \pm \sqrt {4 + 16} } \over 2} \\ \\ & = {{2 \pm \sqrt {20} } \over 2} \\ \\ & = {{2 \pm \sqrt 4 \cdot \sqrt 5 } \over 2} \\ \\ & = {{2 \pm 2 \cdot \sqrt 5 } \over 2} \\ \\ {x_1} &= {{2 + 2 \cdot \sqrt 5 } \over 2} \\ \\ & = {2 \over 2} + {2 \over 2}\sqrt 5 \\ \\ & = \boxed {\color{red}1 + \sqrt 5} \\ \\ {x_2} &= {{2 – 2 \cdot \sqrt 5 } \over 2} \\ \\ & = {2 \over 2} – {2 \over 2}\sqrt 5 \\ \\ & = \boxed{\color{red}1 – \sqrt 5} \end{align*}Thus, the answers are [latex]{x_1} = 1 + \sqrt 5 [/latex] and [latex]{x_2} = 1 – \sqrt 5 [/latex].
Problem 9: Solve the quadratic equation using the quadratic formula.
[latex]{\left( {2x – 1} \right)^2} = \Large{x \over 3}[/latex]
Answer
If we carefully transform the given quadratic equation into the standard form, we get [latex]12{x^2} – 13x + 3 = 0[/latex].
\begin{align*} & a = 12 \\ & b = – 13 \\ & c = 3 \\ \\ x &= {{ – b \pm \sqrt {{b^2} – 4ac} } \over {2a}} \\ \\ & = {{ – \left( { – 13} \right) \pm \sqrt {{{\left( { – 13} \right)}^2} – 4\left( {12} \right)\left( 3 \right)} } \over {2\left( {12} \right)}} \\ \\ & = {{13 \pm \sqrt {169 – 144} } \over {24}} \\ \\ & = {{13 \pm \sqrt {25} } \over {24}} \\ \\ & = {{13 \pm 5} \over {24}} \\ \\ {x_1} &= {{13 + 5} \over {24}} \\ \\ & = {{18} \over {24}} \\ \\ & = \boxed {\color{red}{3 \over 4}} \\ \\ {x_2} &= {{13 – 5} \over {24}} \\ \\ & = {8 \over {24}} \\ \\ & =\boxed {\color{red} {1 \over 3}} \end{align*}Therefore, the answers are [latex]x_1={\Large{3 \over 4}}[/latex] and [latex]x_2={\Large{1 \over 3}}[/latex].
Problem 10: Solve the quadratic equation using the quadratic formula.
[latex]\left( {2x – 1} \right)\left( {x + 4} \right) = – {x^2} + 3x[/latex]
Answer
If we simplify the quadratic equation to convert it to the standard form, we should arrive at [latex]3{x^2} + 4x – 4 = 0[/latex].
\begin{align*} & a = 3 \\ & b = 4 \\ & c = – 4 \\ \\ x &= {{ – b \pm \sqrt {{b^2} – 4ac} } \over {2a}} \\ \\ & = {{ – \left( 4 \right) \pm \sqrt {{{\left( 4 \right)}^2} – 4\left( 3 \right)\left( { – 4} \right)} } \over {2\left( 3 \right)}} \\ \\ & = {{ – 4 \pm \sqrt {16 + 48} } \over 6} \\ \\ & = {{ – 4 \pm \sqrt {64} } \over 6} \\ \\ & = {{ – 4 \pm 8} \over 6} \\ \\ {x_1} &= {{ – 4 + 8} \over 6} \\ \\ & = {4 \over 6} \\ \\ & = \boxed {\color{red}{2 \over 3}} \\ \\ {x_2} &= {{ – 4 – 8} \over 6} \\ \\ & = {{ – 12} \over 6} \\ \\ & = \boxed {\color{red} – 2} \end{align*}Hence, the answers are [latex]x_1={\Large{2 \over 3}}[/latex] and [latex]x_2=-2[/latex].
You may also be interested in these related math lessons or tutorials: