How to Solve Quadratic Equations using the Square Root Method
This is the “best” method whenever the quadratic equation only contains [latex]{x^2}[/latex] terms. That implies no presence of any [latex]x[/latex] term being raised to the first power somewhere in the equation.
The general approach is to collect all [latex]{x^2}[/latex] terms on one side of the equation while keeping the constants to the opposite side. After doing so, the next obvious step is to take the square roots of both sides to solve for the value of [latex]x[/latex]. Always attach the [latex] \pm [/latex] symbol when you get the square root of the constant.
Examples of How to Solve Quadratic Equations by Square Root Method
Example 1: Solve the quadratic equation below using the Square Root Method.

I will isolate the only [latex]{x^2}[/latex] term on the left side by adding both sides by [latex] + 1[/latex]. Then solve the values of [latex]x[/latex] by taking the square roots of both sides of the equation. As I mentioned before, we need to attach the plus or minus symbol to the square root of the constant.
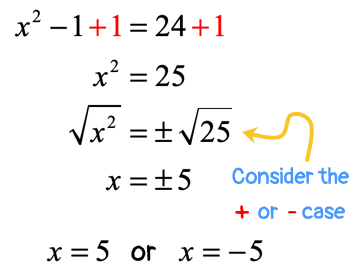
So I have [latex]x = 5[/latex] and [latex]x = – \,5[/latex] as final answers since both of these values satisfy the original quadratic equation. I will leave it to you to verify.
Example 2: Solve the quadratic equation below using the Square Root Method.
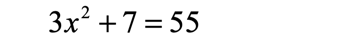
This problem is very similar to the previous example. The only difference is that after I have separated the [latex]{x^2}[/latex] term and the constant in the opposite sides of the equation, I need to divide the equation by the coefficient of the squared term before taking the square roots of both sides.

The final answers are [latex]x = 4[/latex] and [latex]x = – \,4[/latex].
Example 3: Solve the quadratic equation below using the Square Root Method.
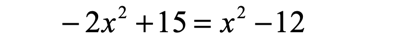
I can see that I have two [latex]{x^2}[/latex] terms, one on each side of the equation. My approach is to collect all the squared terms of [latex]x[/latex] to the left
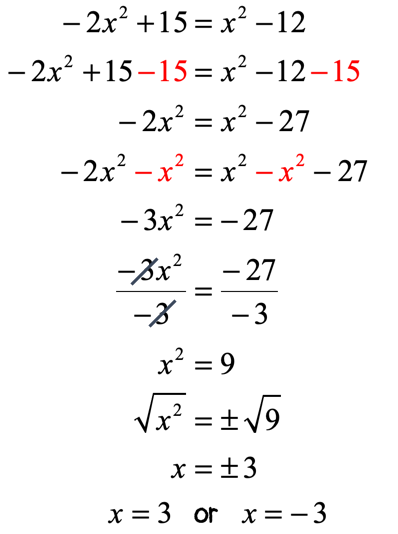
The solutions to this quadratic formula are [latex]x = 3[/latex] and [latex]x = – \,3[/latex].
Example 4: Solve the quadratic equation below using the Square Root Method.
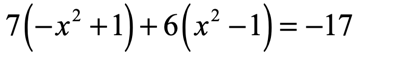
The two parentheses should not bother you at all. The fact remains that all variables come in the squared form, which is what we want. This problem is perfectly solvable using the square root method.
So my first step is to eliminate both of the parentheses by applying the distributive property of multiplication. Once they are gone, I can easily combine like terms. Keep the [latex]{x^2}[/latex] terms to the left, and constants to the right. Finally, apply square root operation in both sides and we’re done!
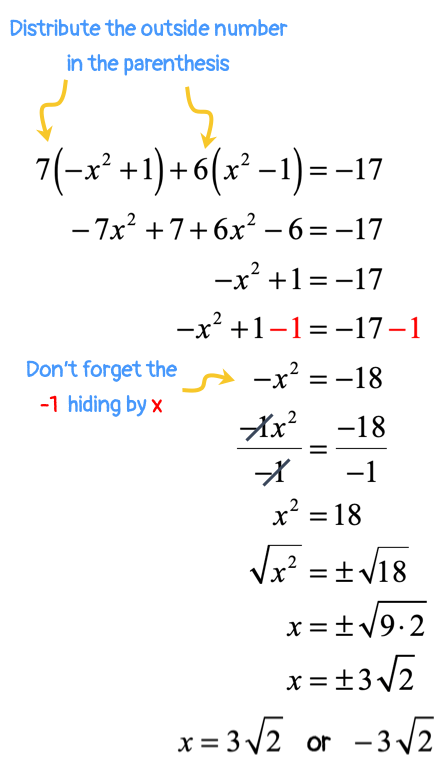
Not too bad, right?
Example 5: Solve the quadratic equation below using the Square Root Method.
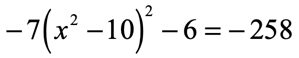
Since the [latex]x[/latex]-term is being raised to the second power twice, that means, I need to perform two square root operations in order to solve for [latex]x[/latex].
The first step is to have something like this: ( )2 = constant. This allows me to get rid of the exponent of the parenthesis on the first application of square root operation.
After doing so, what remains is the “stuff” inside the parenthesis which has an [latex]{x^2}[/latex] term. Well, this is great since I already know how to handle it just like the previous examples.

There’s an [latex]x[/latex]-squared term left after the first application of square root.
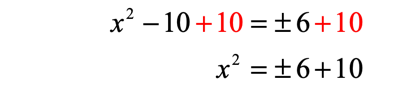
Now we have to break up [latex]{x^2} = \pm \,6 + 10[/latex] into two cases because of the “plus” or “minus” in [latex]6[/latex].
- Solve the first case where [latex]6[/latex] is positive.
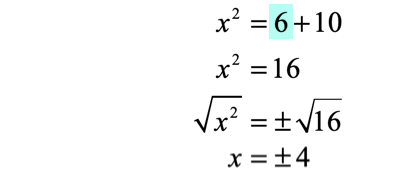
- Solve the second case where [latex]6[/latex] is negative.
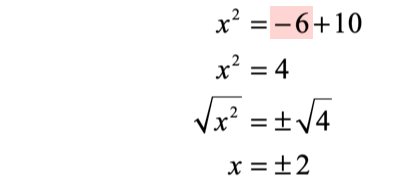
The solutions to this quadratic equations are [latex]x = 4[/latex], [latex]x = – \,4[/latex], [latex]x = 2[/latex], and [latex]x = – \,2[/latex]. Yes, we have four values of [latex]x[/latex] that can satisfy the original quadratic equation.
Example 6: Solve the quadratic equation below using the Square Root Method.
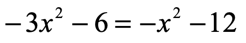
Solution:
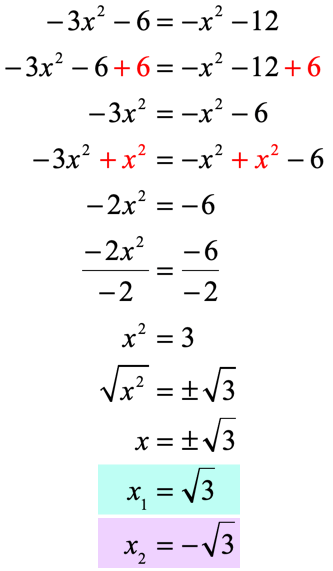
Example 7: Solve the quadratic equation below using the Square Root Method.
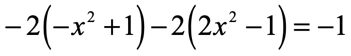
Solution:
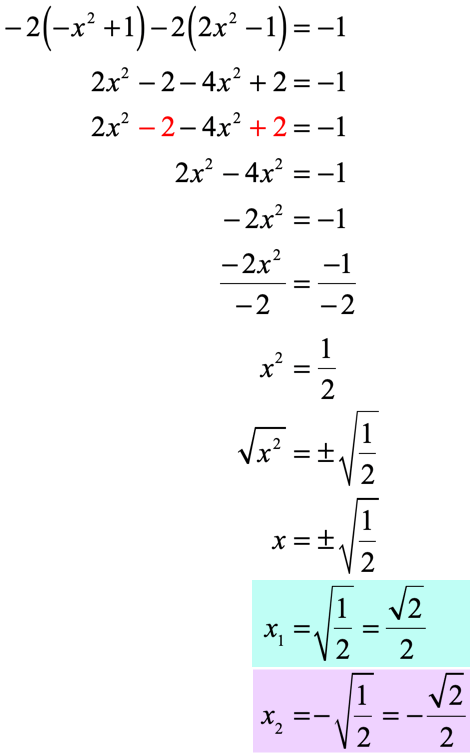
You may also be interested in these related math lessons or tutorials:
Solving Quadratic Equations by Factoring Method
Solving Quadratic Equations by the Quadratic Formula
Solving Quadratic Equations by Completing the Square
