How to Solve Quadratic Equations using Factoring Method
This is the easiest method of solving a quadratic equation as long as the binomial or trinomial is easily factorable. Otherwise, we will need other methods such as completing the square or using the quadratic formula.
The following diagram illustrates the main approach to solving a quadratic equation by factoring method.
Main Idea of using Factoring Method to Solve a Quadratic Equation
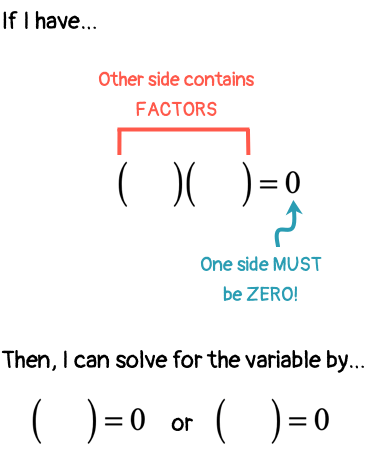
The diagram above suggests the following key points:
- One side of the equation is just zero.
- The opposite side should contain the factors of the given polynomial.
- After the two conditions stated above are met, then it is now OKAY to set each factor equal to zero then solve for the value of the unknown variable.
Examples of How to Solve Quadratic Equations using the Factoring Method
Example 1: Solve the quadratic equation below by Factoring Method.
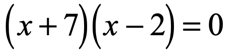
I consider this type of problem as a “freebie” because it is already set up for us to find the solutions. Notice that the left side contains factors of some polynomial, and the right side is just zero!
What we need to do is simply set each factor equal to zero, and solve each equation for [latex]x[/latex].
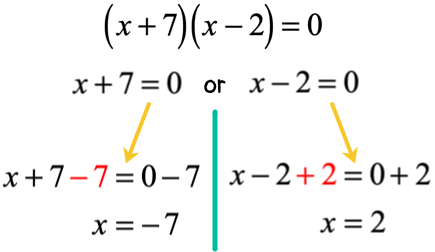
The answers are [latex]x = – \,7[/latex] and [latex]x = 2[/latex]. You may back-substitute these values of [latex]x[/latex] to the original equation to verify if they are true answers. I will leave it to you as an exercise.
Example 2: Solve the quadratic equation below by Factoring Method.
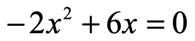
The left side of the equation is a binomial. That means I can pull out a monomial factor. If you think about it, between the numerical coefficients [latex] – \,2[/latex] and [latex]6[/latex], I can factor out [latex] – \,2[/latex]. More so, between [latex]{x^2}[/latex] and [latex]x[/latex], I can factor out [latex]x[/latex]. So to find the overall factor (it’s like finding the GCF), I will multiply [latex] – \,2[/latex] and [latex]x[/latex] to get [latex] – \,2x[/latex].
Note, I can also factor out [latex]2x[/latex] instead of [latex] – \,2x[/latex]. The final answer should be the same. Try it out!
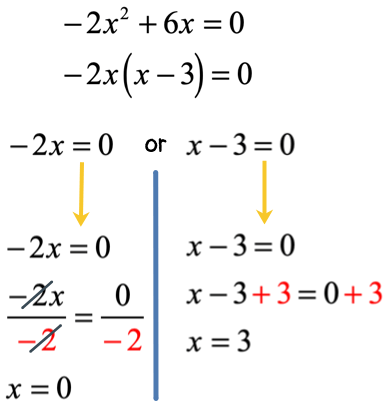
Example 3: Solve the quadratic equation below using the Factoring Method.
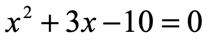
Have you factored a trinomial before where the coefficient of the squared term is [latex] + 1[/latex]? If not, it is very simple.
To factor this trinomial into two binomials, I need to find two numbers (by trial and error) that satisfy two given conditions:
- The product of these two numbers is equal to the constant term (last number) which is [latex] – 10[/latex].
- The sum of these two numbers is equal to the coefficient of the linear term which is [latex] + 3[/latex].

Since the product of two numbers is negative, I know that these numbers must have opposite signs. More so, having a sum of positive number implies that the number with the larger absolute value must be positive.
If you work it out mentally or using paper and pencil to run through possible combinations, the two numbers that can satisfy the given conditions are [latex] + 5[/latex] and [latex] – 2[/latex].
To check, their products [latex]\left( { + \,5} \right)\left( { – \,2} \right) = – 10[/latex], and their sum [latex]\left( { + \,5} \right)\,\, + \,\,\left( { – \,2} \right) = + 3[/latex]. Works out great!
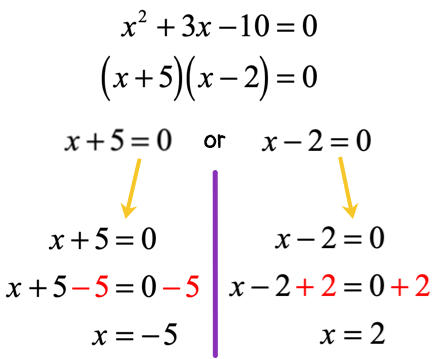
The final solutions are [latex]x = – \,5[/latex] and [latex]x = 2[/latex].
Example 4: Solve the quadratic equation below using the Factoring Method.
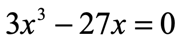
Between the coefficients [latex]3[/latex] and [latex] – 27[/latex], I can pull out [latex]3[/latex]. And between [latex]{x^3}[/latex] and [latex]x[/latex], I can take out [latex]x[/latex]. Therefore the overall expression that I can factor out is their product: [latex]\left( 3 \right)\left( x \right) = 3x[/latex].
Notice that after I factored out [latex]3x[/latex], I am left with a “special” binomial called the “Difference of Two Squares” which is very easy to factor.
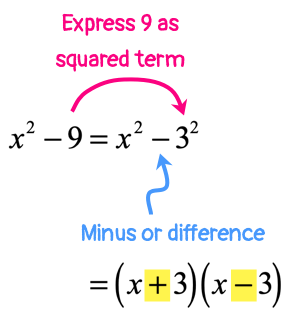
It is always the case that the middle signs will be opposites (see yellow).
Here is the complete solution.
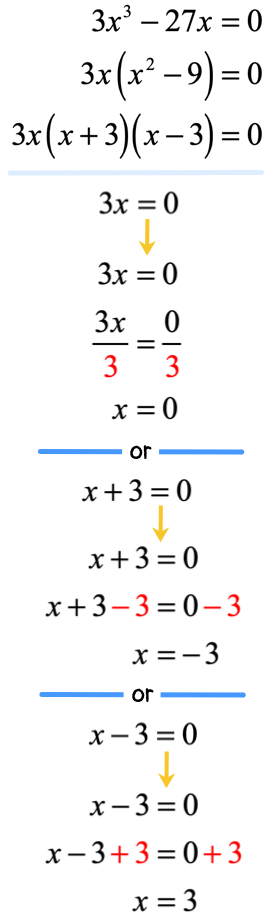
You should back-substitute to verify that [latex]x = 0[/latex], [latex]x = – \,3[/latex], and [latex]x = 3[/latex] are the correct solutions.
Example 5: Solve the quadratic equation below using the Factoring Method.
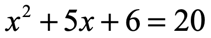
The first thing I realize in this problem is that one side of the equation doesn’t contain zero. I can easily create a zero on the right side by subtracting both sides by [latex]20[/latex].
After doing so, the left side should have a factorable trinomial that is very similar to problem 3.
To factor out this trinomial, think of two numbers when multiplied together gives [latex] – 14[/latex] (constant term) and when added gives [latex] + 5[/latex] (coefficient of [latex]x[/latex]-term). By trial and error, the numbers should be [latex] – 2[/latex] and [latex]7[/latex]. You may verify this correct combination.
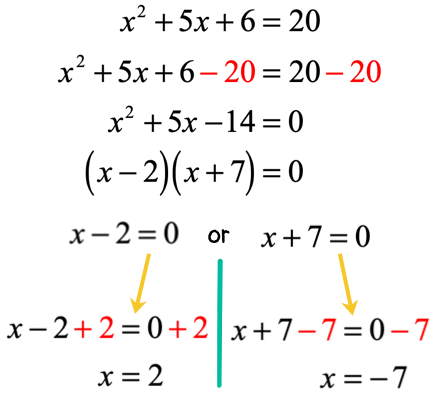
The final answers are [latex]x = 2[/latex] and [latex]x = – \,7[/latex].
Example 6: Solve the quadratic equation below using the Factoring Method.
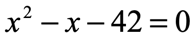
Solution:
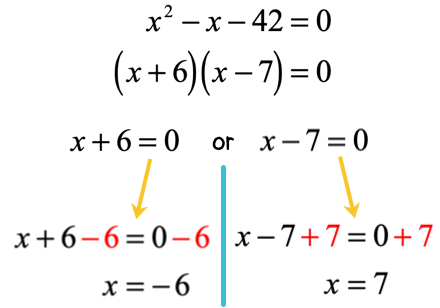
Here we have [latex]x = – \,6[/latex] and [latex]x = 7[/latex] as our final answers.
Example 7: Solve the quadratic equation below using the Factoring Method.
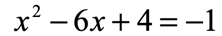
Solution:
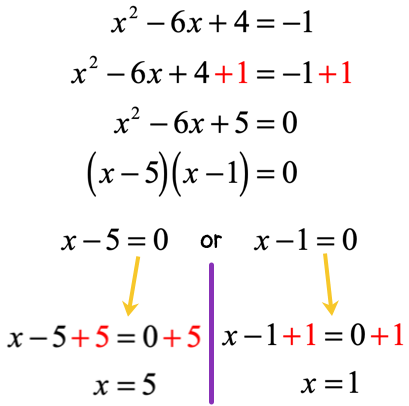
Our final answers are [latex]x = 5[/latex] and [latex]x = 1[/latex].
Example 8: Solve the quadratic equation below using the Factoring Method.
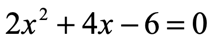
Solution:
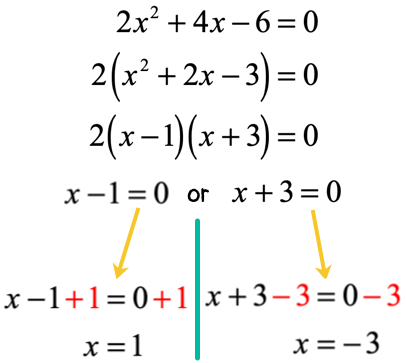
The final solutions are [latex]x = 1[/latex] and [latex]x = – \,3[/latex].
You may also be interested in these related math lessons or tutorials:
Solving Quadratic Equations by Square Root Method
Solving Quadratic Equations by the Quadratic Formula
Solving Quadratic Equations by Completing the Square
