Inverse of a 2×2 Matrix Formula

In this lesson, we are only going to deal with 2×2 square matrices. I have prepared five (5) worked examples to illustrate the procedure on how to solve or find the inverse matrix using the Formula Method.

Just to provide you with the general idea, two matrices are inverses of each other if their product is the identity matrix. An identity matrix with a dimension of 2×2 is a matrix with zeros everywhere but with 1’s in the diagonal. It looks like this.

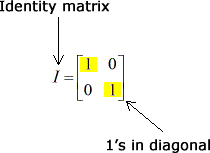
A 2x2 identity matrix with ones in the diagonal. The identity matrix is usually represented by the uppercase letter "I". It has the elements 1 and 0 on the first row, and elements 0 and 1 on the second row.

It is important to know how a matrix and its inverse are related by the result of their product. So then,

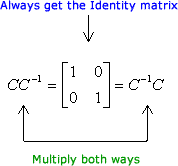
If a 2×2 matrix A is invertible and is multiplied by its inverse (denoted by the symbol A⁻¹), the resulting product is the Identity matrix which is denoted by [latex]I[/latex]. To illustrate this concept, see the diagram below.

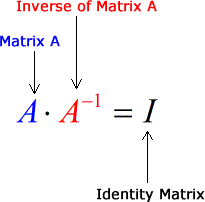
Matrix A when multiplied by its inverse written as A^-1 is equal to the identity matrix I. We can express this is short form as A * A^-1 = I.

In fact, I can switch the order or direction of multiplication between matrices A and A⁻¹, and I would still get the Identity matrix [latex]I[/latex]. That means invertible matrices are commutative.

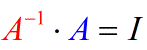
If A is an invertible matrix then A and its inverse, A^-1, are commutative under the operation of matrix multiplication. That means A times A^-1 and A^-1 times A will have the same product which is the identity matrix I. In the equation forms, we can express these algebraic relationships as A*A^-1=I and A^-1*A=I.

How do we find the inverse of a matrix? The formula is rather simple. As long as you follow it, there shouldn’t be any problem. Here we go.

The Formula to Find the Inverse of a 2×2 Matrix

Given the matrix A

Matrix A is a 2 by 2 matrix with entries a and b on its first row, and entries c and d on its second row. We can write this in matrix form as A = [a,b;c,d].

Its inverse is calculated using the formula

The formula to find the inverse of an invertible matrix A involves by first calculating the determinant of matrix A and rearranging matrix A from [a,b;c,d] to [d,-b;-c,a]. Now use the scalar value of 1 over determinant of matrix to multiply the rearranged elements of matrix A which is [d,-b;-c,a]. In compact form, the inverse of matrix A or A^-1 = (1/det A) [d,-b;-c,a].

where [latex]\color{red}{\rm{det }}\,A[/latex] is read as the determinant of matrix A.

A few observations about the formula:

Entries [latex]\color{blue}a[/latex] and [latex]\color{blue}d[/latex] from matrix A are swapped or interchanged in terms of position in the formula.
Entries [latex]\color{blue}b[/latex] and [latex]\color{blue}c[/latex] from matrix A remain in their current positions, however, the signs are reversed. In other words, put negative symbols in front of entries [latex]b[/latex] and [latex]c[/latex].
Since [latex]\color{red}{\rm{det }}\,A[/latex] is just a number, then [latex]\large{1 \over {{\rm{det }}A}}[/latex] is also a number that would serve as the scalar multiplier to the matrix

See my separate lesson on scalar multiplication of matrices.

Examples of How to Find the Inverse of a 2×2 Matrix

Example 1: Find the inverse of the 2×2 matrix below, if it exists.

Matrix A is a 2x2 matrix with entries 5 and 2 on the first row, and entries -7 and -3 on the second row. Therefore, A = [5,2;-7,-3].

The formula requires us to find the determinant of the given matrix. Do you remember how to do that? If not, that’s okay. Review the formula below on how to solve for the determinant of a 2×2 matrix.

Let matrix A be A = [a,b;c,d] then its determinant is calculated as det A = (a)(d) minus (b)(c)

So then, the determinant of matrix A is

here's the step by step solution to find the determinant of a 2 by 2 square matrix A with elements 5 and 2 on its first row, and elements -7 and -3 on its second row. det A = det [5,2;-7,-3] = (5)(-3) - (2)(-7) = -15 + 14 = -1. Therefore the determinant of matrix A is negative 1.

To find the inverse, I just need to substitute the value of [latex]{\rm{det }}A = – 1[/latex] into the formula and perform some “reorganization” of the entries, and finally, perform scalar multiplication.

Here goes again the formula to find the inverse of a 2×2 matrix.

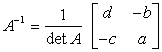
the general formula to find the inverse of matrix A is A^-1 = (1/det A) multiplied as the scalar factor to the matrix with elements d and -b on the first row, and entries -c and on the second row

Now, let’s find the inverse of matrix A.

A^-1 = (1/-1) times [-3,-2; 7,5] = (-1) times = [3,2;-7,-5]. So the inverse of matrix A has entries 3 and 2 on the first row and entries -7 and -5 on the second row.

Let’s then check if our inverse matrix is correct by performing matrix multiplication of A and A⁻¹ in two ways, and see if we’re getting the Identity matrix.

this shows that matrix A when multiplied by its inverse A^-1 results to the identity matrix I. in the same manner, when the inverse of matrix A when multiplied to matrix A also gives the identity matrix which means that they are commutative under the operation of matrix multiplication. Therefore, AA^-1 = [5,2;7,-3] [3,2;-7,-5} = [1,0;0,1].

Furthermore when changing the order of multiplication also gives the identity matrix. Thus, A^-1A = [3,2;-7,-5] [5,2;-7,-3] = [1,0;0,1].

Since multiplying both ways generate the Identity matrix, then we are guaranteed that the inverse matrix obtained using the formula is the correct answer!

Example 2: Find the inverse of the 2×2 matrix below, if it exists.

matrix B has elements -3 and 1 on the first row, and has elements 5 and -2 on the second row. We can write this compact form as B = [-3,1;5,-2].

First, find the determinant of matrix B.

the determinant of matrix B = [-3,1;5,-2] is equal to (-3)(-2) minues (1)(5) = 6 - 5 =1. so the final answer is det B = -1.

Secondly, substitute the value of det B = 1 into the formula, and then reorganize the entries of matrix B to conform with the formula.

here's the step by step solution to find the inverse of the 2x2 square matrix B. B^-1 = (1/det B) times [d,-b;-c,a] = (1/1) times [-2,-1;-5,-3] =[-2,-1;-5,-3]. So the final is that the inverse of matrix B has -2 and -1 on the first row, and -5 and -3 on the second row.

I will leave it to you to verify that

this matrix equation illustrates that matrix B multiplied to its inverse, and vice versa, gives the identity matrix I with elements 1 and 0 on the first row, and 0 and 1 on the second row. Therefore, we can write this as B*B^-1 = B^-1*B = [1,0;0,1]

In other words, the matrix product of B and B⁻¹ in either direction yields the Identity matrix.

Example 3: Find the inverse of the matrix below, if it exists.

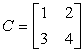
matrix C is a 2x2 matrix that has an inverse that means it is invertible. matrix C has entries 1 and 2 on its first row, and entries 3 and 4 on its second row

This is a great example because the determinant is neither [latex]+1[/latex] nor [latex]−1[/latex] which usually results in an inverse matrix having rational or fractional entries. I must admit that the majority of problems given by teachers to students about the inverse of a 2×2 matrix is similar to this.

Step 1: Find the determinant of matrix C.

The formula to find the determinant

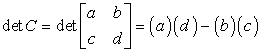
determinant of matrix C is equal to the difference of the product of "a" and "d"; and the product of "b" and "c"

Below is the animated solution to calculate the determinant of matrix C

this is an animated GIF solution to find the determinant of matrix C which will be used to find its inverse matrix. det C = det [1,2;3,4] = (1)(4) - (2)(3) = 4 - 6 = -2

Step 2: The determinant of matrix C is equal to [latex]−2[/latex]. Plug the value in the formula then simplify to get the inverse of matrix C.

to find the inverse of 2x2 matrix C, first, we obtain the determinant of matrix C. we found it to be -1/2. now we multiply (-1/2) to the rearranged matrix C we swapped the positions of elements a and d, and get the opposites of elements b and c. we show that C^-1 = (-1/2)* = [-2,1;3/2,-1/2].

Step 3: Check if the computed inverse matrix is correct by performing left and right matrix multiplication to get the Identity matrix.

C times C^-1 is equal to C^-1 times C which is the identity matrix with entries 1 and 0 on the first row, and 0 and 1 on the second row. this again illustrates that if C is invertible that the product of C and its inverse is always the same even if we change the order of matrix multiplication

Yep, matrix multiplication works in both cases as shown below.

First case:

Second case:

C^-1 times C is the identity matrix [1,0;0,1]

Example 4: Find the inverse of the matrix below, if it exists.

matrix D is a 2 by 2 square matrix that contains the elements of 4 and 2 on its first row, and the elements of 2 and 1 on its second row. in compact form, matrix D = [4,2;2,1]

In our previous three examples, we were successful in finding the inverse of the given [latex]2 \times 2[/latex] matrices. I don’t want to give you the impression that all [latex]2 \times 2[/latex] matrices have inverses.

In this example, I want to illustrate when a given [latex]2 \times 2[/latex] matrix fails to have an inverse. How does that happen?

If we review the formula again, it is obvious that this situation can occur when the determinant of the given matrix is zero because 1 divided by zero is undefined. And so, an undefined term distributed into each entry of the matrix does not make any sense.

this shows what happens when the determinant of a 2x2 matrix is zero which means that the matrix doesn't have an inverse since any number divided by zero is undefined

Let’s go back to the problem to find the determinant of matrix D.

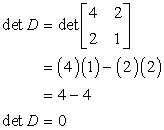
matrix D is an example where the determinant is zero. matrix D has elements 4 and 2 on its first row, and elements 2 and 1 on its second row. det D = (4)(1) - (2)(2) = 4-4 = 0. Therefore det D = 0 which makes matrix D not to have an inverse matrix, in other words, matrix D is non-invertible matrix

Therefore, the inverse of matrix D does not exist because the determinant of D equals zero. This is our final answer!

Example 5: Find the inverse of the matrix below, if it exists.

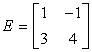
matrix E has elements 1 and -1 on the first row, and elements 3 and 4 on the second row

Step 1: Find the determinant of matrix E.

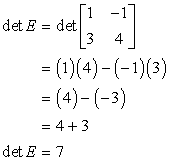
the determinant of matrix E is 7 since det E =(1)(4) - (-1)(3) = 4 - (-3) = 4 + 3 = 7.

Step 2: Reorganize the entries of matrix E to conform with the formula, and substitute the solved value of the determinant of matrix E. Distribute the value of [latex]\large{1 \over {{\rm{det }}E}}[/latex] to the entries of matrix E then simplify, if possible.