Matrix Multiplication: Product of Two Matrices

Matrix multiplication is the “messy type” because you will need to follow a certain set of procedures in order to get it right. This is the “messy type” because the process is more involved. However, you will realize later after going through the procedure and some examples that the steps required are manageable. Don’t worry, I will help you with this!

But first, we need to ensure that the two matrices are “allowed” to be multiplied together. Otherwise, the given two matrices are “incompatible” to be multiplied. If this is the case, we say that the solution is undefined.

Matrix to Matrix Multiplication a.k.a “Messy Type”

Always remember this!

In order for matrix multiplication to work, the number of columns of the left matrix MUST EQUAL to the number of rows of the right matrix.

Suppose we are given the matrices [latex]A[/latex] and [latex]B[/latex], find [latex]AB[/latex] (do matrix multiplication, if applicable). Determine which one is the left and right matrices based on their location. It is a very important step.

There are two matrices here namely A and B. In A*B, matrix A is the left matrix while matrix B is the right matrix. Matrix A is a 3 by 2 matrix with elements [-5,1;0,2;7,1] while matrix B is a 3 by 3 matrix with entries [6,-1,4;0,1,-5;8,0,0].

To determine if I can multiply the two given matrices, I need to pay attention to the number of columns of matrix [latex]A[/latex] and the number of rows of matrix [latex]B[/latex]. If they are equal, then I can proceed with Matrix Multiplication. Otherwise, I will conclude that the answer is undefined!

Because Matrix A has the number of columns of 2, and Matrix B has the number of rows of 3, and they are not equal (2 ≠ 3), I conclude that [latex]AB[/latex] = undefined. That means their product can’t be found.

Examples of Matrix Multiplication a.k.a. “Messy Type”

Directions: Given the following matrices, perform the indicated operation.

Matrix A, a 3 by 3 square matrix, contains the entries -5, 2 and 0 on its first row, entries of 7, -3 and 4 on its second row, and entries -1, 3, and 2 on its third row. That is, matrix A =[-5,2,0;7,-3,4;-1,3,2].
Matrix B, a 2 by 3 rectangular matrix, has entries 8, 1, and 2 on the first column, and entries -5, 6, and 7 on the second column. We can write this rectangular matrix as B = [8,1,2;-5,6,7].
Matrix C is a 3 by 3 square matrix with elements 0,-1, and 8 on the first row, elements 6,-14, and 2 on the second row, and elements 9,5 and 1 on the third row. Matrix C = [0,-1,8;6,-14,2;9,5,1].
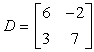
Matrix D is a 2 by 2 square matrix where the elements on the first row are 6 and -2, and the elements on the second row are 3 and 7.
Matrix E is a 3 by 2 rectangular matrix that contains elements of -5 and 1 on its first row, elements of 0 and 2 on its second row, and elements of -11 and 7 on its third row. Matrix E = [-5,1;0,2;-11,7].
Matrix F is a 2 by 2 square matrix with entries 1 and -2 on the first row, and entries -3 and 4 on the second row. Matrix F can be expressed as F = [1,-2;-3,4].

Example 1: Calculate, if possible, the product of [latex]B[/latex] and [latex]E[/latex].

In order for matrices [latex]B[/latex] and [latex]E[/latex] to have a product, the number of columns of left matrix B must equal the number of rows of right matrix E.

  • Matrix B (left)
Matrix B has 2 rows and 3 columns. The entries on the first row are 8, 1 and 2. The entries on the second row are -5, 6 and 7. Therefore, Matrix B = [8,1,2;-5,5,7].

number of columns = 3

  • Matrix E (right)
Matrix E has 3 rows and 2 columns. The first row contains the elements -5 and 1. The second row contains the elements 0 and 2. The third row contains the elements -11 and 7. Matrix E = [-5,1;0,2;-11,7].

number of rows = 3

Since this is the case, then it is okay to multiply them together. Now, these are the steps:

Step 1: Place them side by side.

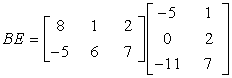
Matrix B is being multiplied to matrix E. We can find the product of matrices B and E because the number of columns of matrix B is equal to the number of rows of matrix E. Matrix B has entries 8, 1 and 2 on its first row, and entries -5, 6 and 7 on the second row. Matrix E contains elements -5 and 1 on the 1st row, 0 and 2 on the 2nd row, and -11 and 7 on the 3rd row.

Step 2: Multiply the rows of [latex]B[/latex] into the columns of [latex]E[/latex] by multiplying the corresponding elements of each row to each element of the column, and then add them together.

Please watch the animated solution carefully.

This is an animated GIF file showing how to find the product of matrices B and E where matrix B is the left matrix and matrix E is the right matrix. When you multiply matrix B by matrix E, the product is a 2 by 2 square matrix with entries -62 and 24 on the first row and entries -52 and 56 on the second row. That is B*E = [-62,24;-52,56].

If you have no patience watching the animated solution above on how to perform matrix multiplication, you can view the regular solution I have included below.

This is a more compact way or method in finding the product of matrix B and E. Thus, B times E = [8,1,2;-5,6,7] times [-5,1;0,2;-11,7] = [-62,24; -52;56].

Example 2: Calculate, if possible, the product of [latex]E[/latex] and [latex]F[/latex].

Check first if the product of the two matrices exists by making sure that the number of columns of left matrix E equals the number of rows of right matrix F.

  • Matrix E (left)
Matrix E is a rectangular matrix because the number of rows does not equal to the number columns. Matrix E has three rows and two columns. We can write matrix E is compact form as E = [-5,1;0,2;-11,7].

number of columns = 2

  • Matrix F (right)
Matrix F is a square matrix because the number of rows is equal to the number of columns. Matrix F has two rows and two columns. We can write it in symbolic form as F=[1,-2;-3,4].

number of rows = 2

This is wonderful since the number of columns of matrix [latex]E[/latex] equals the number of rows of matrix [latex]F[/latex]. This means the product of [latex]EF[/latex] is defined so we can go ahead and perform matrix multiplication. See below for the animated step-by-step solution of matrix multiplication.

This is an animated GIF image that shows the product of matrices E and F where matrix E is the left matrix while F is the right matrix. This step by step solution in multiplying matrix E to matrix F yields a product of a rectangular matrix with entries -8 and 14 on its first 1st row, entries 6 and 8 on its 2nd row, and entries -32 and 50 on its 3rd row. Therefore, we can write the final product as EF = [-8,14;-6,8;-32,50].

Example 3: Calculate, if possible, the product of [latex]F[/latex] and [latex]E[/latex].

In our previous example, we have successfully obtained the product of [latex]EF[/latex]. This time around, we want to find if we can find the product of [latex]E[latex] and [latex]F[/latex], in that order.

Just to remind you, real numbers are commutative under multiplication operation which means that the order of multiplication does not affect the final product. For instance…

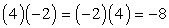
(4)(-2)=(-2)(4)=-8

So the big question becomes, does it work also in matrix multiplication?

Is the product of matrices E and F (E is the left matrix and F is the right matrix) is equal to the product of matrices F and E (F is the left matrix and E is the right matrix)? That is, is EF = FE ?

Let’s check if the number of columns of matrix F equals the number of rows of matrix [latex]E[/latex].

  • Matrix F (left)
The left matrix F is a two by two square matrix with elements 1 and -2 on the first row, and elements -3 and 4 on the second row. We write matrix F in symbolic form as F=[1,-2;-3,4].

number of columns = 2

  • Matrix E (right)
The right matrix E is a three by two rectangular matrix with elements -5 and 1 on the first row, elements 0 and 2 on the second row, and elements -11 and 7 on the third row. Matrix E can be expressed as E=[-5,1;0,2;-11,7].

number of rows = 3

Obviously, the number of columns of Matrix [latex]F[/latex] does not equal the number of rows of Matrix [latex]E[/latex]. The implication is that the product of [latex]FE[/latex] cannot be calculated, and therefore undefined!

In general, matrix multiplication is not commutative.

Example 4: Calculate, if possible, the product of [latex]AE[/latex].

The standard way to describe the size or dimension of a matrix is to…

(state number of rows) x (state number of columns)

…read as “the number of rows by the number of columns”.

Matrix A is a square matrix by with a dimension of 3 by 3. The first row contains the elements -5, 2 and 0. The second row contains the elements of 7, -3 and 4. Finally, the third row contains the elements -1, 3 and 2. This can be written as A = [-5,2,0;7,-3,4;-1,3,2].

3 x 3 (three by three matrix)

Matrix E is a rectangular matrix by with a dimension of 3 by 2. The first row contains the elements -5 and 1. The second row contains the elements of 0 and 4. Finally, the third row contains the elements -11 and 7. This can be written as A = [-5,1;0,2;-11,7].

3 x 2 (three by two matrix)

Since the number of columns of matrix A equals the number of rows of matrix E then we conclude that the product of [latex]AE[/latex] is defined.

Let’s work it out. See the animated solution below.

This is an animated GIF image showing how to find the product of matrix A and matrix E. The product of matrices A and E is defined since the number of columns of matrix A is 3 which is equal to the number of rows of matrix E. The final product is a three by two rectangular matrix with entries of 25 and -1 on its first row, entries of -79 and 29 on its second row, and entries of -17 and 19 on its third row. Therefore, A*E=[25,-1;-79,29;-17,19].

Example 5: Calculate, if possible, the product of [latex]E[/latex] and [latex]A[/latex].

Matrix E has a dimension of 3x2 which means that it is a rectangular matrix. It contains the elements of -5 and 1 on the first row, elements of 0 and 2 on the second row, and elements -11 and 7 on the third row. Therefore, we can write this matrix as E = [-5,1;0,2;-11,7].

3 x 2 (three by two matrix)

Matrix A has a dimension of 3x3 which means that it is a square matrix. It contains the elements of -5, 2, and 0 on the first row, elements of 7, -3, and 4 on the second row, and elements -1, 3 and 2 on the third row. We can write this matrix as A = [-5,2,0;7,-3,4;-1,3,2].

3 x 3 (three by three matrix)

Obviously, the number of columns of matrix E does not equal the number of columns of matrix A. Therefore, the product of [latex]EA[/latex] cannot be calculated, or undefined.

Example 6: Calculate, if possible, the product of [latex]D[/latex] and [latex]F[/latex].

Since the number of columns of matrix [latex]D[/latex] equals the number of rows of matrix [latex]F[/latex], the product of [latex]DF[/latex] is defined.

Matrices D and F are multiplied. Since both matrices have the same dimension or size, that is both 2 by 2 matrix, their product is defined. The product of matrices D and F is a 2x2 matrix with elements 12 and -20 on the first row, and elements -18 and 22 on the second row. That means, D*F=[12,-20;-18,22].

Example 7: What is the product of matrix C when multiplied by itself?

This is rather simple. We will simply multiply matrix [latex]C[/latex] by matrix [latex]C[/latex] which can be written as [latex]CC[/latex] or [latex]{C^2}[/latex]. In other words, we are squaring matrix [latex]C[/latex].

We need to be cautious here. Notice that only a square matrix can be squared. Just to remind you, a square matrix is a matrix where the number of its row is equal to the number of its column.

I will leave it to you to verify that the solution below is correct. For math problems such as this, although tedious, I always recommend doing it by hand using a pencil and paper.

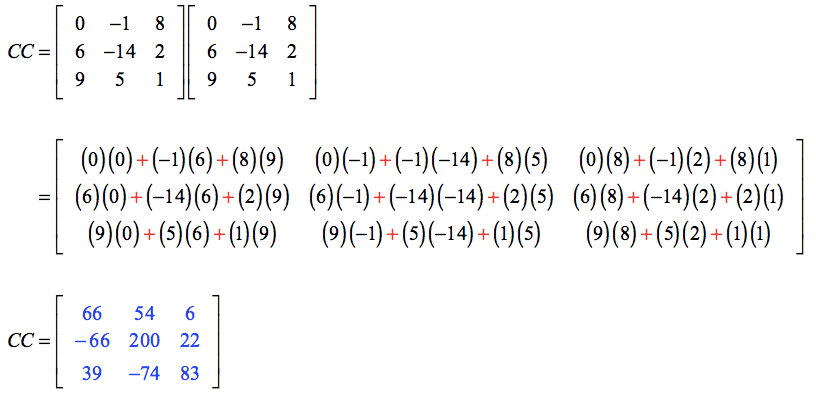
The product of matrices C and C is a 3 by 3 matrix with elements 66, 54, and 6 on the first row; -66, 200, and 22 on the second row, and 39, -74, and 83 on the third row.

You may also be interested in these related math lessons or tutorials:

Adding and Subtracting Matrices

Scalar Multiplication