Finding the Inverse of an Exponential Function
I will go over three examples in this tutorial showing how to determine algebraically the inverse of an exponential function. But before you take a look at the worked examples, I suggest that you review the suggested steps below first in order to have a good grasp of the general procedure.
Steps to Find the Inverse of an Exponential Function
STEP 1: Change [latex]f\left( x \right)[/latex] to [latex]y[/latex].
[latex]\large{f\left( x \right) \to y}[/latex]
STEP 2: Interchange [latex]\color{blue}x[/latex] and [latex]\color{red}y[/latex] in the equation.
[latex]\large{x \to y}[/latex]
[latex]\large{y \to x}[/latex]
STEP 3: Isolate the exponential expression on one side (left or right) of the equation.
The exponential expression shown below is a generic form where [latex]b[/latex] is the base, while [latex]N[/latex] is the exponent.
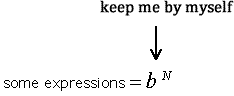
STEP 4: Eliminate the base [latex]b[/latex] of the exponential expression by taking the logarithms of both sides of the equation.
- To make the simplification much easier, take the logarithm of both sides using the base of the exponential expression itself.
- Using the log rule,
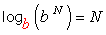
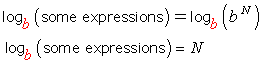
STEP 5: Solve the exponential equation for [latex]\color{red}y[/latex] to get the inverse. Finally, replace [latex]\color{red}y[/latex] with the inverse notation [latex]{f^{ – 1}}\left( x \right)[/latex] to write the final answer.
Replace [latex]y[/latex] with [latex]{f^{ – 1}}\left( x \right)[/latex]
Let’s apply the suggested steps above to solve some problems.
Examples of How to Find the Inverse of an Exponential Function
Example 1: Find the inverse of the exponential function below.
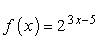
This should be an easy problem because the exponential expression on the right side of the equation is already isolated for us.
Start by replacing the function notation [latex]f\left( x \right)[/latex] by [latex]y[/latex].
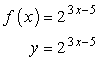
The next step is to switch the variables [latex]\color{red}x[/latex] and [latex]\color{red}y[/latex] in the equation.
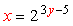
Since the exponential expression is by itself on one side of the equation, we can now take the logarithms of both sides. When we get the logarithms of both sides, we will use the base of [latex]\color{blue}2[/latex] because this is the base of the given exponential expression.
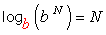
Apply the Log of Exponent Rule which is [latex]{\log _b}\left( {{b^k}} \right) = k[/latex] as part of the simplification process. The rule states that the logarithm of an exponential number where its base is the same as the base of the log is equal to the exponent.
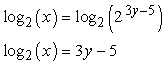
We are almost done! Solve for [latex]y[/latex] by adding both sides by [latex]5[/latex] then divide the equation by the coefficient of [latex]y[/latex] which is [latex]3[/latex]. Don’t forget to replace [latex]y[/latex] to [latex]{f^{ – 1}}\left( x \right)[/latex]. This means that we have found the inverse function.
![[log base 2 of (x)] plus 5 over 3 is equal to f raised to negative 1 (x)](https://www.chilimath.com/wp-content/uploads/2017/02/581.png)
If we graph the original exponential function and its inverse on the same [latex]XY-[/latex] plane, they must be symmetrical along the line [latex]\large{\color{blue}y=x}[/latex]. Which they are!
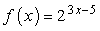
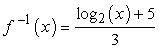
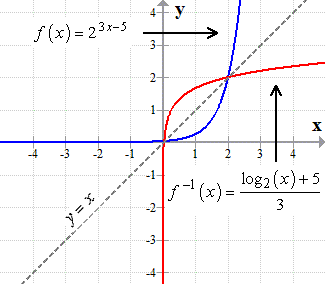
Example 2: Find the inverse of the exponential function below.
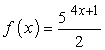
The only difference of this problem from the previous one is that the exponential expression has a denominator of [latex]2[/latex]. Other than that, the steps will be the same.
We change the function notation [latex]f\left( x \right)[/latex] to [latex]y[/latex], followed by interchanging the roles of [latex]\color{red}x[/latex] and [latex]\color{red}y[/latex] variables.
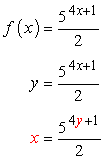
At this point, we can’t perform the step of taking the logarithms of both sides just yet. The reason is that the exponential expression on the right side is not fully by itself. We first have to get rid of the denominator [latex]2[/latex].
We can accomplish that by multiplying both sides of the equation by [latex]2[/latex]. The left side becomes [latex]2x[/latex] and the denominator on the right side is gone!
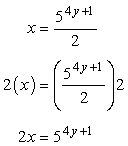
By isolating the exponential expression on one side, it is now possible to get the logs of both sides. When you do this, always make sure to use the base of the exponential expression as the base of the logarithmic operations.
In this case, the base of the exponential expression is [latex]5[/latex]. Therefore, we apply log operations on both sides using the base of [latex]5[/latex].
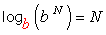
Using this log rule, [latex]{\log _b}\left( {{b^k}} \right) = k[/latex] , the fives will cancel out leaving the exponent [latex]\color{blue}4x+1[/latex] on the right side of the equation after simplification. This is great since the log portion of the equation is gone.
We can now finish this up by solving for the variable [latex]y[/latex], then replacing that by [latex]{f^{ – 1}}\left( x \right)[/latex] to denote that we have obtained the inverse function.
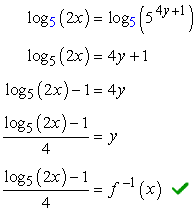
As you can see, the graphs of the exponential function and its inverse are symmetrical about the line [latex]\large{\color{green}y=x}[/latex].
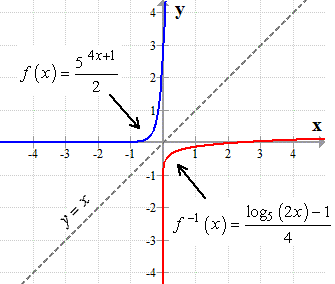
Example 3: Find the inverse of the exponential function below.
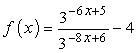
I see that we have an exponential expression being divided by another. The good thing is that the exponential expressions have the same base of [latex]3[/latex]. We should be able to simplify this using the Division Rule of Exponent. To divide exponential expressions having equal bases, copy the common base and then subtract their exponents. Below is the rule. The assumption is that [latex]b \ne 0[/latex].
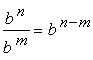
Observe how the original problem has been greatly simplified after applying the Division Rule of Exponent.
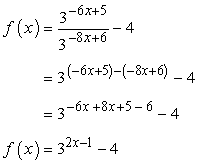
At this point, we can proceed as usual in solving for the inverse. Rewrite [latex]f\left( x \right)[/latex] as [latex]y[/latex], followed by interchanging the variables [latex]\color{red}x[/latex] and [latex]\color{red}y[/latex].
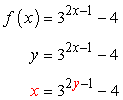
Before we can get the logs of both sides, isolate the exponential portion of the equation by adding both sides by [latex]4[/latex].
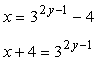
Since the exponential expression is using base [latex]3[/latex], we take the logs of both sides of the equation with base [latex]3[/latex] as well! By doing so, the exponent [latex]\color{blue}2y-1[/latex] on the right side will drop, so we can continue on solving for [latex]y[/latex] which is the required inverse function.
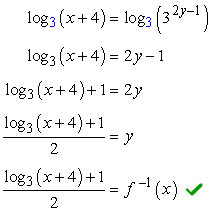
It verifies that our answer is correct because the graph of the given exponential functions and its inverse (logarithmic function) are symmetrical along the line [latex]\large{y=x}[/latex].
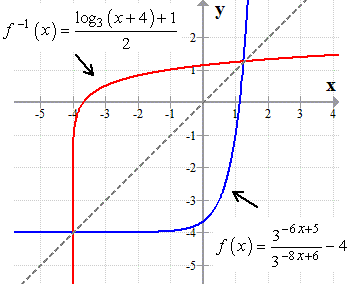
You may also be interested in these related math lessons or tutorials:
Inverse of Absolute Value Function
