Rules or Laws of Exponents
In algebra, it’s crucial to understand the rules governing exponents, often referred to as the exponent rules. By mastering these fundamental principles, as well as the foundational rules of logarithms (commonly termed “log rules“), we set ourselves up for a more productive and engaging algebraic journey. These foundational skills underpin many advanced concepts, making them indispensable in our future math studies.
Let’s start by studying the parts of an exponential number.
An exponential number or expression is composed of two parts. The first component is the base which “carries” the exponent which is the second component on its upper right corner.
Take a look at the illustration below.
Parts of an Exponential Number or Expression

For instance, how would you write [latex]2 \cdot 2 \cdot 2 \cdot 2 \cdot 2[/latex] in exponential notation?
The number [latex]2[/latex] is the number being multiplied repeatedly and so it automatically becomes the base of the exponential expression. Notice that it is written five times. This value specifies the number of occurrences of the base, thus, this must be the exponent.
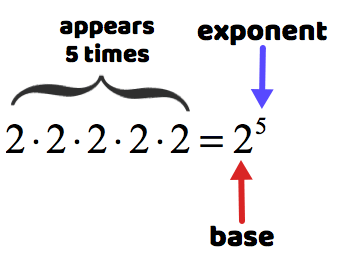
Read as “2 to 5th power”.
The base of an exponential expression can also be a letter or variable. Suppose we have
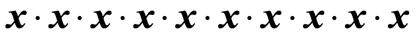
Since the variable [latex]x[/latex] is multiplying itself ten times, we can write this in a compact form.
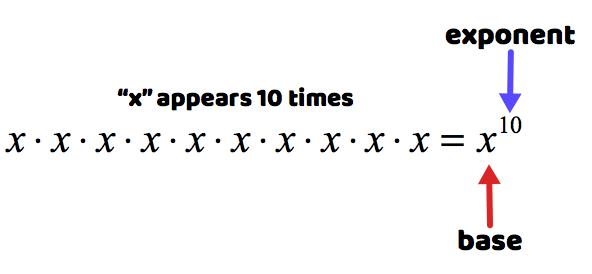
Read as “[latex]x[/latex] to the 10th power”.
Quick Summary of the Seven (7) Exponent Rules or Laws
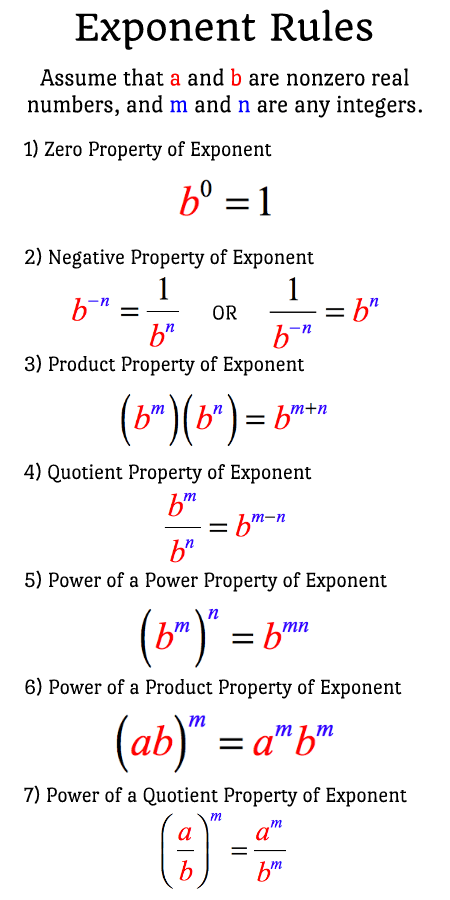
Now, let’s go over the seven (7) basic exponent rules or laws.
Description of Each Exponent Rule with Examples
RULE 1: Zero Exponent Property
[latex]{b^0} = 1[/latex]
Any nonzero number raised to zero power is equal to 1.
Examples:
- Simplify the exponential expression [latex]{5^0}[/latex].
We have a nonzero base of [latex]5[/latex], and an exponent of zero. The zero rule of exponent can be directly applied here. Thus, [latex]{5^0} = 1[/latex].
- Simplify the exponential expression [latex]{\left( {2{x^2}y} \right)^0}[/latex].
The base here is the entire expression inside the parenthesis, and the good thing is that it is being raised to the zero power. Caution, as long as the variable [latex]x[/latex] or [latex]y[/latex] is not equal to zero, we can definitely apply the zero rule of exponent here as well. This gives us [latex]{\left( {2{x^2}y} \right)^0} = 1[/latex].
- Simplify the exponential expression below.
![5[(x^3)^0]/15[(y^3)^0]](https://www.chilimath.com/wp-content/uploads/2018/12/exponential-expression-1.png)
Each expression with a parenthesis raised to the power of zero, [latex]0[/latex], both found in the numerator and denominator will simply be replaced by [latex]1[/latex]. Make sure to reduce the fraction to its lowest term.
![[5(x^3)^0/[15(y^3)^0 = [5(1)]/[15(1)] = 5/15 = 1/3](https://www.chilimath.com/wp-content/uploads/2020/01/soluton-to-exponential-expression-1.gif)
RULE 2: Negative Exponent Property
![b^(-n) = 1/(b^n) or 1/[b^(-n)] = b^n](https://www.chilimath.com/wp-content/uploads/2018/12/negative-rule.png)
Any nonzero number raised to a negative exponent is not in standard form. We will need to do some rearranging. Move the base with a negative exponent to the opposite side of the fraction, then make the exponent positive. The assumptions here are [latex]b \ne 0[/latex] and [latex]n[/latex] is an integer.
Examples:
- Simplify the exponential expression [latex]{2^{ – \,4}}[/latex].
The base [latex]2[/latex] has a negative exponent of [latex]-4[/latex]. This can be fixed by moving it to the denominator and switching the sign of the exponent to positive using the negative rule of
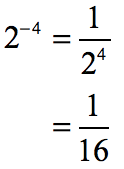
- Simplify the exponential expression.
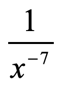
This time the base with a negative exponent is found in the denominator. Bring it up to the numerator while making the exponent positive.
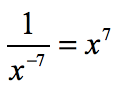
- Simplify the exponential expression.
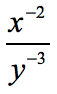
Both of the exponents in the numerator and denominator are negative. It should make sense to swap their locations along the fractional bar. The [latex]x[/latex]-variable goes down, while the [latex]y[/latex]-variables goes up! Make sure to change both their exponents to positive.
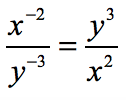
RULE 3: Product Property of Exponent
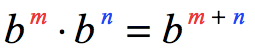
When multiplying exponential expressions with the same base where the base is a nonzero real number, copy the common base then add their exponents. The assumptions here are [latex]b \ne 0[/latex] and [latex]m[/latex] and [latex]n[/latex] are any integers.
Examples:
- Simplify the product of exponential expressions [latex]\left( {{x^6}} \right)\left( {{x^2}} \right)[/latex].
We are multiplying two exponentials with the same base, [latex]x[/latex]. The product allows us to combine them by copying the common base, and then adding their exponents. Remember that the assumption here is that the common base is a nonzero real number.
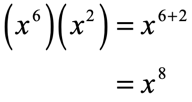
- Simplify the product of exponential expressions [latex]\left( {2{x^3}{y^9}} \right)\left( {7{x^2}{y^2}} \right)[/latex].
Observe that each parenthesis contains a number, [latex]x[/latex]-variable, and [latex]y[/latex]-variable. Make sure to multiply the terms of the same kind only. That is, multiply the numbers together, and multiply each kind of variable separately. To emphasize this step, we will group them first before applying the product rule.
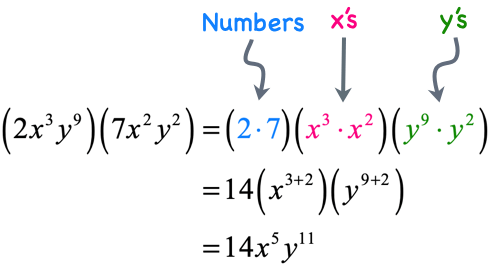
- Simplify the product of exponential expressions [latex]\left( {{x^6}{y^{ – \,2}}} \right)\left( {{x^{ – 13}}{y^2}} \right)[/latex].
After we multiply the exponential expressions with the same base by adding their exponents, we arrive at having one variable with a negative exponent, and another with zero exponent.
Don’t hesitate to apply the two previous rules learned, namely Rule 1 and Rule 2, to further simplify this expression.
![[x^6 y^(-2)] [x^(-13) y^2] = x^(6-13) y^(-2+2) = x^-7 y^0 = 1/x^7](https://www.chilimath.com/wp-content/uploads/2019/03/rexp-rule3c.png)
RULE 4: Quotient Property of Exponent
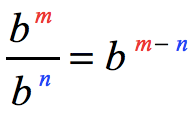
When dividing exponential expressions with the same base where the base is a nonzero real number, copy the common base then subtract the top exponent by the bottom exponent. We must suppose here that [latex]b \ne 0[/latex] and both [latex]m[/latex] and [latex]n[/latex] belong to the set of integers.
Examples:
- Simplify the quotient of exponential expressions.
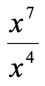
The fractional bar implies that we are going to divide. It makes sense to apply the Division Rule of Exponent, that is, copy the common base in the numerator and denominator and subtract the top exponent by the lower exponent.
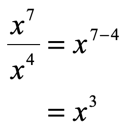
- Simplify the exponential expressions.
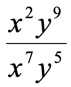
Comparing the expressions in the numerator and the denominator, I see that there are two common bases, [latex]x[/latex] and [latex]y[/latex]. Apply the division rule on each variable. After doing so, the [latex]x[/latex]-variable will contain a negative exponent, therefore, use the negative rule of
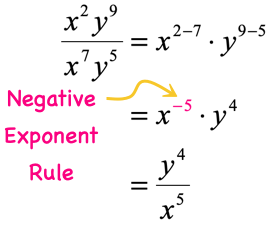
- Simplify the exponential expressions.
![[(x^-9)(y^3)]/[(x^-7)(y^8)]](https://www.chilimath.com/wp-content/uploads/2019/03/rexp-rule4e.png)
One way to simplify this is to ignore the negative exponents for now. Apply the division rule first, and see if negative exponents show up again. If that’s the case, utilize the negative rule of exponent.
![[(x^-9)(y^3)]/[(x^-7)(y^8)]= x^(-9+7) y^(-5) = 1/(x^2y^5)](https://www.chilimath.com/wp-content/uploads/2019/03/rexp-rule4-f.png)
RULE 5: Power of a Power Property of Exponent
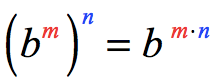
When an exponential expression is raised to a power, copy the base which is a nonzero real number, then multiply the inner and outer exponents. We assume here that [latex]b \ne 0[/latex] and both m and n are integers.
Example:
- Simplify the exponential expression [latex]{\left( {{x^5}} \right)^3}[/latex].
This expression has inner and outer exponents. The Power to a Power Rule allows us to copy the base and multiply the exponents.
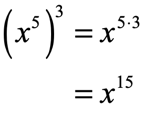
RULE 6: Power of a Product Property of Exponent
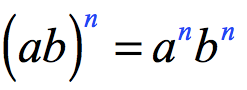
When a product of two or more factors is raised to a power, copy each factor then multiply its exponent to the outer exponent. We have to do it for each factor inside the parenthesis which in this case are a and b. The assumptions are [latex]a \ne 0[/latex] or [latex]b \ne 0[/latex], and [latex]n[/latex] is an integer.
Example:
- Simplify the exponential expression [latex]{\left( {{2^3}{x^7}{y^6}} \right)^2}[/latex].
This problem is very similar to the previous one. The only difference is that there are three (3) factors with exponents. We just need to distribute the outer exponent to each of the inner exponents.
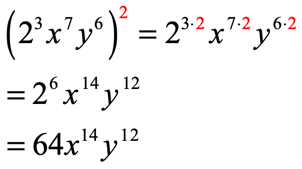
RULE 7: Power of a Quotient Property of Exponent
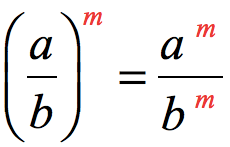
When a quotient is raised to a power, copy the factor on the numerator then multiply its exponent to the outer exponent. We must do the same with the factor in the denominator where we copy it and then multiply its exponent to the outer exponent. Here, we also need to assume that [latex]a \ne 0[/latex] or [latex]b \ne 0[/latex], and [latex]m[/latex] is an integer.
Example:
- Simplify the exponential expression.
![[(3x^4)/(y^6)]^3](https://www.chilimath.com/wp-content/uploads/2019/03/rexp-rule7a.png)
Actually, we will simultaneously use two properties of exponents here in order to simplify this completely. On top of Rule 7 (Power of a Quotient Rule), we will need to apply Rule 6 (Power of a Product Rule). In simple terms, just treat the numerator and denominator separately when distributing by multiplication the inner and outer exponents for each factor.
![[(3x^4)/(y^6)]^3 = (3^3 x^12)/(y^18) = (27x^12)/(y^18)](https://www.chilimath.com/wp-content/uploads/2019/03/rexp-rule7b.png)
You may also be interested in these related math lessons or tutorials:
