“Inverse” of Constant Function
A constant function has the general form f\left( x \right) = {\color{red}a} where \color{red}a is a real number.
From the general formula, the output of a constant function regardless of its input value (usually denoted by x), will always be the same which is the fixed number \color{red}a.
How to Find the Inverse of a Constant Function
Suppose we have a constant function f\left( x \right) = 2. The graph of this function is just a horizontal line (parallel to the x-axis) passing through the point \color{blue}(0, 2).
Now, we can find its inverse algebraically by doing the following steps:
- Given:
f\left( x \right) = 2
- Replace f\left( x \right) by y.
y = 2
- Swap the roles of x and y to get the inverse function:
x=2
The graph of \color{red}x=2 is just a vertical line (parallel to the y-axis) passing through the point (2, 0). Here are the graphs of the original constant function and its inverse on the same XY-axis,
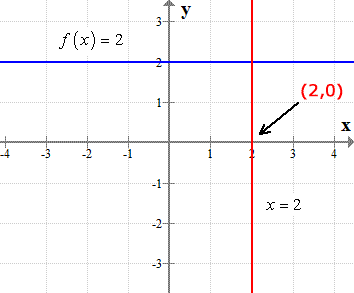
They are truly inverses of each other because they are symmetrical about the line \large{\color{green}y=x}. Observe that their graphs are mirror images of each other along that line.
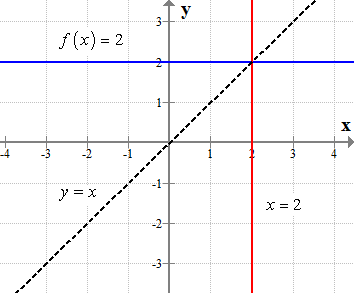
However, is the vertical line x=2 a function? The answer is NO. Since every vertical line would fail the vertical line test. If we draw a vertical line cutting through x=2 it will intersect at it more than once. In fact, they will overlap thus intersecting at an infinite number of points.
So in summary, the inverse of any constant function will always be a vertical line which is not a function. Therefore, every constant function has no inverse that is a function!
You might also be interested in:
Inverse of Absolute Value Function
Inverse of Exponential Function