Finding the Inverse Function of a Rational Function
Finding the inverse of a rational function is relatively easy. Although it can be daunting at first, you will get comfortable as you study along. In this lesson, I have prepared five (5) examples to help you gain a basic understanding on how to approach it. You may realize later that the procedure to find the inverse is rather repetitious. That means, once you get the hang of it, you got it! Not a bad thing, right?
Keep in mind that the method used here is just one way out of the many. Feel free to vary the steps to fit your needs as long as you’re getting the same final answer.
Key Steps in Finding the Inverse Function of a Rational Function
- Replace [latex]f\left( x \right)[/latex] by [latex]y[/latex].
- Switch the roles of [latex]\color{red}x[/latex] and [latex]\color{red}y[/latex], in other words, interchange [latex]x[/latex] and [latex]y[/latex] in the equation.
- Solve for [latex]y[/latex] in terms of [latex]x[/latex].
- Replace [latex]y[/latex] by [latex]\color{blue}{f^{ – 1}}\left( x \right)[/latex] to get the inverse function.
Examples of How to Find the Inverse of a Rational Function
Example 1: Find the inverse function. State its domain and range.
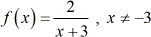
Even without graphing this function, I know that [latex]x[/latex] cannot equal [latex]-3[/latex] because the denominator becomes zero, and the entire rational expression becomes undefined. In fact, the domain is all [latex]x-[/latex]values not including [latex]-3[/latex].
Next, I need to graph this function to verify if it passes the Horizontal Line Test so I can be guaranteed to have an inverse function. I don’t want to “waste” effort if I am absolutely sure that I am towards a dead end.
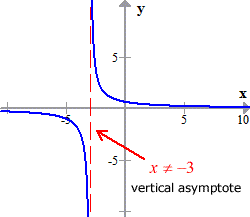
It seems that no horizontal line will intersect the graph more than once. That’s a good sign. The vertical dashed line is called a vertical asymptote. The graph will never cross that. Remember, it is coming from the zeros of the denominator, or the restricted values of [latex]x[/latex].
Using the suggested steps, let’s find the inverse.
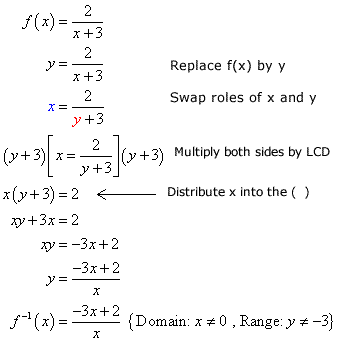
The domain of the inverse function comes from the fact that the denominator cannot equal zero. The range is obtained from the domain of the original function.
Example 2: Find the inverse function. State its domain and range.
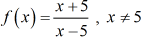
I may not need to graph this because the numerator and denominator of the rational expression are both linear. Based on experience, I am sure that this will have an inverse because it can pass the Horizontal Line Test. The rest of the work is simply algebraic. But here’s the graph anyway.
As you solve, you will encounter terms with variable [latex]y[/latex] on both sides of the equation. Your task is to move all the [latex]y-[/latex]terms on the left (though you can gather them on the right), and then factor out the [latex]y[/latex] to single it out.
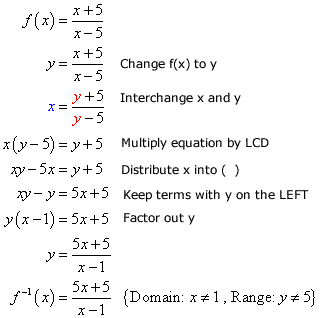
Since I cannot allow having [latex]x = 1[/latex] in the denominator, the domain of the inverse function is all real numbers except [latex]x = 1[/latex]. I took the domain of the original function to make the range of the inverse.
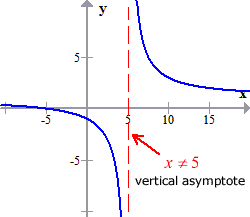
Example 3: Find the inverse function. State its domain and range.
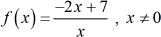
This is the graph of the original function.
The following are the steps to find the inverse.
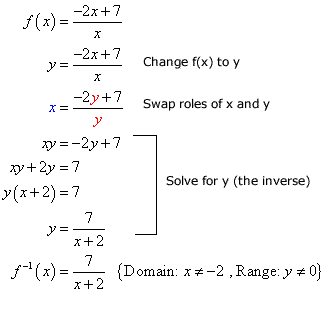
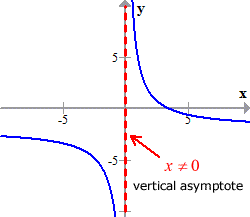
Example 4: Find the inverse function. State its domain and range.
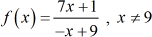
Maybe when you look at this problem, I am positive that you already have the “quick think” on how to approach it. That is usually the nature of any math problem.
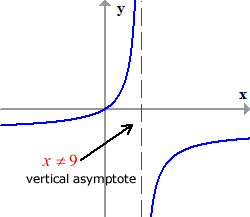
Since the rational expression has linear terms in both numerator and denominator, be convinced that just like in the previous example, it will have an inverse function even without further testing. Add it to your math toolbox and utilize it to your advantage whenever you encounter similar problems. Just to verify, the graph is shown below.
The rest of the steps to find the inverse function is the same. Towards the end of the solution, I cleaned up the final answer by factoring and then canceling the hidden [latex]-1[/latex], found in both numerator and denominator. You will learn how to do it as you gain experience. Or maybe with the use of little common sense.
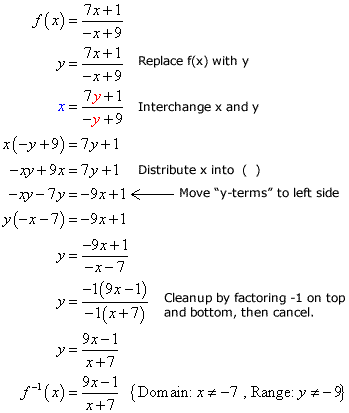
I hope you agree with the domain and range. If not, check out my other lesson about the swapping of domain and range to clarify this further. Remember, the domain and range of a given function, and its inverse are interchanged.
Example 5: Find the inverse function. State its domain and range.
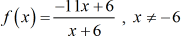
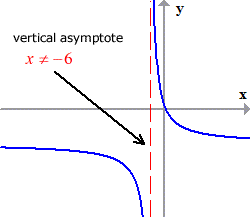
Showing the graph of the original function.
Here are the steps on how to solve for the inverse:
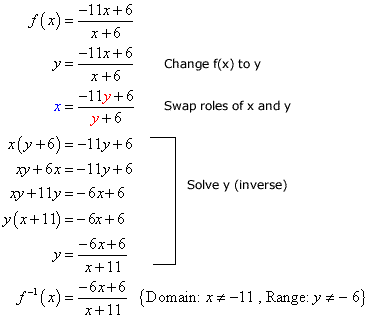
You may also be interested in these related math lessons or tutorials:
Inverse of Absolute Value Function
Inverse of Exponential Function
