Geometric Series Formula
Remember, a sequence is simply a list of numbers while a series is the sum of the list of numbers. A geometric sequence is a type of sequence such that when each term is divided by the previous term, there is a common ratio.
That means, we have [latex]r =\Large {{{a_{n + 1}}} \over {{a_n}}}[/latex] for any consecutive or adjacent terms.
Below is an example of a geometric sequence. Notice that when every term (except the first) is divided by the preceding term, it outputs a common ratio of [latex]2[/latex].
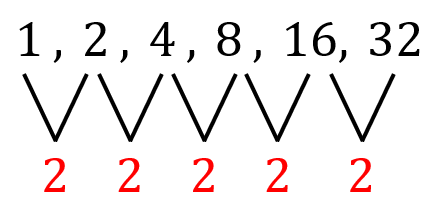
Now, if we add the terms of the sequence, it becomes a series!
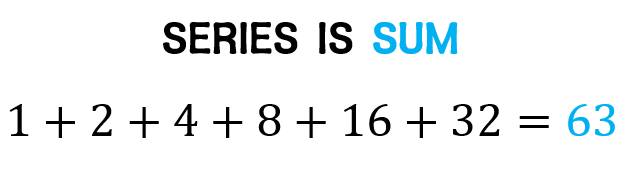
Instead of adding the terms of the sequence by brute force, there is a formula that we can use to easily find the sum of a finite geometric sequence.
![the geometric series formula is given by Sn=a1[(1-r^n)/1-r)] where a1 is the first term, r is the common ratio and n is the number of terms](https://www.chilimath.com/wp-content/uploads/2022/09/geometric-series-formula.png)
Notice that we need three things in order to use the formula. We need the first term, common ratio, and the number of terms. In comparison to the arithmetic series formula, we don’t require the last term.
Let’s go over some examples!
Examples of Geometric Series Formula
Example 1: Find the sum of the first five (5) terms of the geometric sequence.
[latex]2,6,18,54,…[/latex]
This is an easy problem and intended to be that way so we can check it using manual calculation.
First, let’s verify if indeed it is a geometric sequence. Divide each term by the previous term.
[latex]{\Large{{6 \over 2}}} = 3[/latex]
[latex]{\Large{{18} \over 6}} = 3[/latex]
[latex]{\Large{{54} \over {18}}} = 3[/latex]
It has a common ratio of [latex]3[/latex] that means it is a geometric sequence!
We need to add up the first [latex]5[/latex] terms but it looks like we are missing one more term. Let’s generate the fifth term by multiplying the fourth term by the common ratio, thus [latex]54 \times 3 = 162[/latex].
Since we have all the terms in the sequence, we can now add them. We can do it by hand or mental math because they are relatively small numbers.
[latex]2 + 6 + 18 + 54 + 162 = \boxed{242}[/latex]
So we have arrived at [latex]242[/latex]. Let’s use the formula to verify if our answer is correct.
In the geometric sequence, the first term is [latex]2[/latex], the common ratio is [latex]3[/latex] and there are five terms in the sequence that means our [latex]n[/latex] is [latex]5[/latex].
[latex]{a_1} = 2[/latex]
[latex]r = 3[/latex]
[latex]n = 5[/latex]
Substitute these values into the formula then simplify.
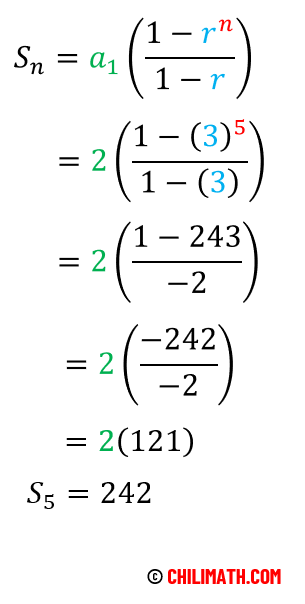
Our answers are the same! Therefore, the sum of the first five terms of the given geometric sequence is [latex]242[/latex].
Example 2: Find the sum of the first ten (10) terms of the geometric sequence if [latex]{a_1} = 3[/latex] and [latex]r=2[/latex].
This problem is straightforward because all the information for the formula are given. Your teacher might give something like this just to check if you know the arithmetic series formula and more importantly, if you know how to use it.
Let’s gather the information that we know.
The first term is [latex]3[/latex], that means [latex]{a_1} = 3[/latex].
The common ratio is [latex]2[/latex], that means [latex]r=2[/latex].
The number of terms is [latex]10[/latex], that means [latex]n=10[/latex].
Plug these values in the formula then simplify.
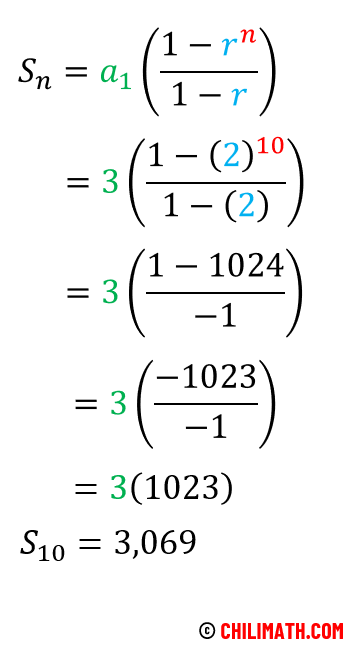
Therefore, the sum of the first ten (10) terms of the geometric sequence is [latex]3,069[/latex].
Example 3: Find the sum of the first six (6) terms of the geometric series.
[latex]36 – 12 + 4 + …[/latex]
If we observe the sequence, the terms are alternating in signs which suggests that the common ratio must be negative. In addition, since the absolute value of the terms are decreasing, it implies that the commo ratio is a fraction.
The first term is obviously [latex]36[/latex].
The common ratio is [latex]\large{ – {1 \over 3}}[/latex] because
[latex]\large{{{ – 12} \over {36}} = – {1 \over 3}}[/latex]
[latex]\large{{4 \over { – 12}} = – {1 \over 3}}[/latex]
We are looking for the sum of the first six terms, thus [latex]n=6[/latex].
Now, we are ready to substitute these values into the formula. Just be careful when dealing with fractions. That’s the only added difficulty in this problem. Other than that, proceed as usual.
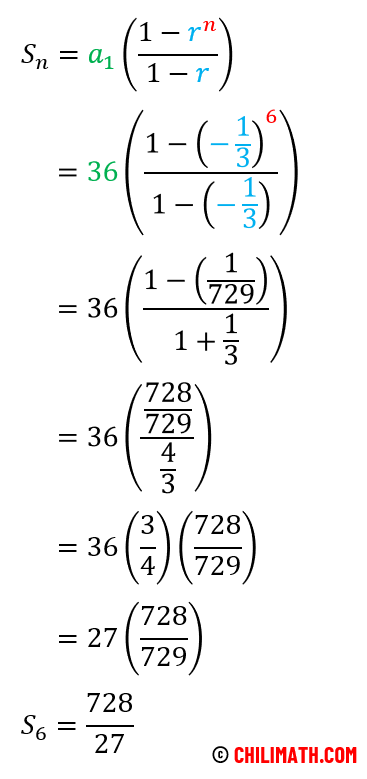
Therefore, the sum of the first six (6) terms of the geometric sequence is [latex]\large{{{728} \over {27}}}[/latex].
Example 4: Find the sum of the geometric series below.
[latex]7 + 21 + 63 + …+15,309[/latex]
At first glance, the problem may look intimidating. But trust me, it is not too bad. When you learn the basic strategy on how to approach this type of problem, you will realize that it is actually very easy. Trust me, you will get it!
Let’s begin by asking what we know. Well, we know the first term which is [latex]7[/latex]. The common ratio is [latex]3[/latex]. Try dividing a term by its preceding term. We should obtain [latex]3[/latex] every time. Another thing is, we don’t know how many terms to add which is the [latex]n[/latex] in the formula. However, the last term is given which is [latex]15,309[/latex]. We will use our previous knowledge regarding geometric sequence to find the number of terms in a sequence [latex]n[/latex] if we know the last term. That’s our plan!
Here’s the geometric sequence formula:
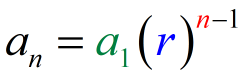
We know the values of the last term which is [latex]a_n=15,309[/latex], first term which is [latex]a_1=7[/latex], and the common ratio which is [latex]r=3[/latex]. Substitute these values in the formula then solve for [latex]n[/latex].
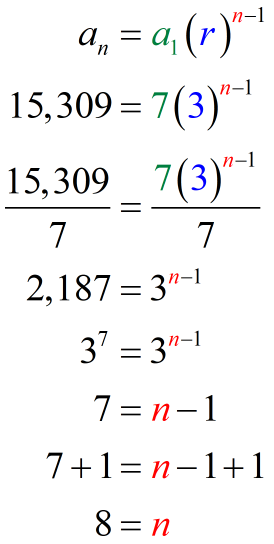
That means there are [latex]8[/latex] terms in the geometric series. We now have all the necessary information to solve the original problem.
Let’s find the first eight (8) terms of the geometric series.
[latex]7 + 21 + 63 + …+15,309[/latex]
The first term is [latex]7[/latex]. The common ratio is [latex]3[/latex]. And there are eight (8) terms in the sequence.
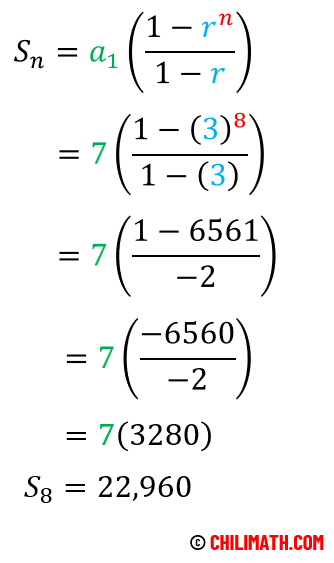
Therefore, the sum of the given geometric series is [latex]22,960[/latex].
Example 5: Find the sum of the geometric series below.
[latex] – 1 + 2 – 4 + … – 4,096[/latex]
This problem is very similar to #4. I just want to do one more problem for mastery.
Let’s identify the relevant information from the given geometric series.
The first term is [latex]-1[/latex]. Because the terms are alternating in signs, we expect the common ratio to be negative.
[latex]{\Large{2 \over { – 1}}} = – 2[/latex]
[latex]{\Large{{ – 4} \over 2}} = – 2[/latex]
So yes, the common ratio is [latex]-2[/latex]. We don’t know the number of terms but we are given the value of the last term which is [latex]-4,096[/latex]. Using the last term, we can take advantage the geometric sequence formula to find the number of terms in the series.
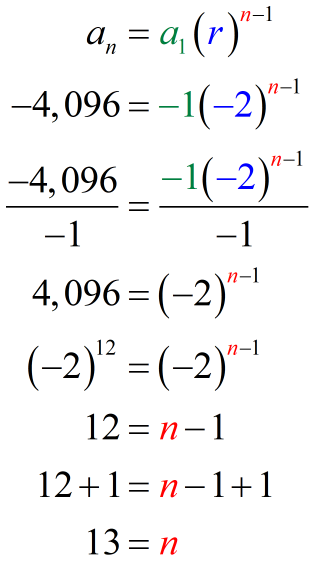
That means there are [latex]13[/latex] terms that we are adding in the series.
Putting it all together, we have [latex]{a_1} = – 1[/latex], [latex]r=-2[/latex] and [latex]n=13[/latex].
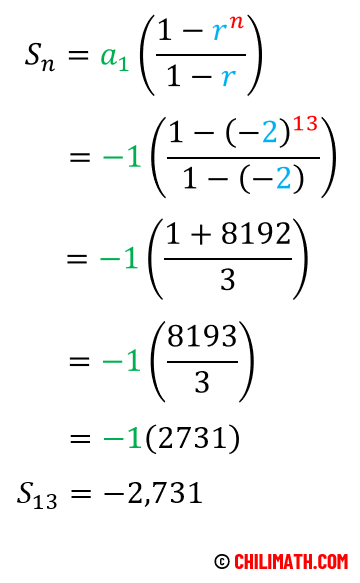
Therefore, the sum of the geometric series is [latex]-2,731[/latex].
Example 6: Find the sum of the geometric series.
[latex]\sum\limits_{n = 1}^9 {2{{\left( 3 \right)}^{n – 1}}}[/latex]
A geometric series can also be written in a compact form using the sigma or sum notation.
The expression above is read as “the sum of [latex]{2{{\left( 3 \right)}^{n – 1}}}[/latex] as [latex]n[/latex] goes from [latex]1[/latex] to [latex]9[/latex].”
Let’s generate some of the few terms in the given geometric series in summation form. To get the first term, begin with [latex]n=1[/latex], substitute that into the formula then simplify. To get the second term, substitute [latex]n=2[/latex] into the formula then simplify. To get the third term, evaluate [latex]n=3[/latex] into the formula, and so on. Skip the middle terms but do the last term, that is, when [latex]n=9[/latex].
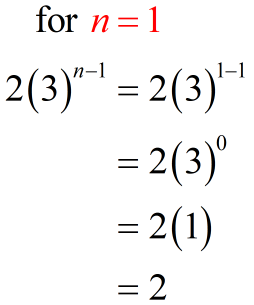
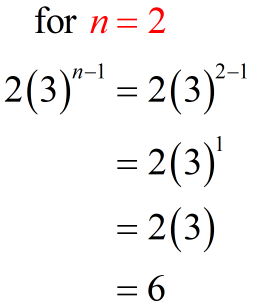
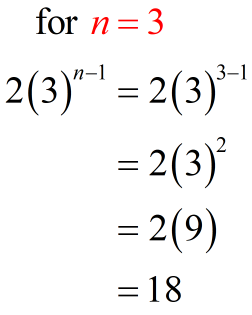
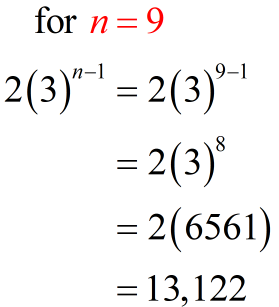
If you have done it right, you should get something similar below.
[latex]\sum\limits_{n = 1}^9 {2{{\left( 3 \right)}^{n – 1}}} = 2 + 6 + 18 + … + 13,122[/latex]
The first term is [latex]2[/latex]. The common ratio is [latex]3[/latex]. And there are [latex]9[/latex] terms in the series.
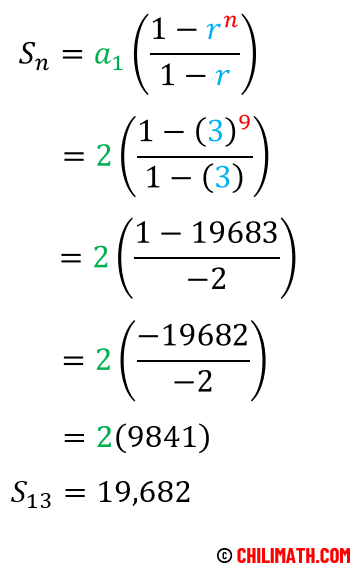
Example 7: Find the second term [latex]{a_2}[/latex] in a geometric series such that [latex]{S_n} ={\large {{2186} \over {81}}}[/latex], [latex]r ={\large {1 \over 3}}[/latex], and [latex]n=7[/latex].
If we examine the geometric series formula, it becomes obvious that we have all the information except the first term [latex]{a_1}[/latex]. By the way, we are solving for [latex]a_1[/latex] so that’s okay. After finding the value of the first term, we can find the second term by simply multiplying the first term by the common ratio.
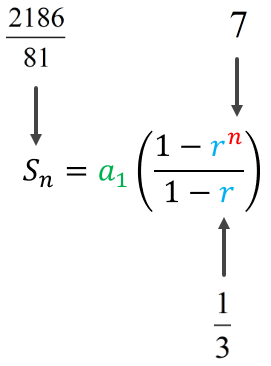
Substitute the known values then solve for [latex]a_1[/latex].

Since the first term is [latex]18[/latex], the second term is found by multiplying the first term by the common ratio.
[latex]{a_2} = {a_1}r = 18\left( {{1 \over 3}} \right) = 6[/latex]
Therefore, the second term is [latex]6[/latex].
You may also be interested in these related math lessons or tutorials:
Geometric Series Practice Problems with Answers
Infinite Geometric Series Formula
