More Practice Problems with the Arithmetic Sequence Formula
Direction: Read each arithmetic sequence question carefully, then answer with supporting details.
Arithmetic Sequence Practice Problems with Answers
1) Tell whether the sequence is arithmetic or not. Explain why or why not.
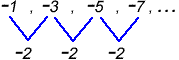
Sequence A : [latex] – 1,{\rm{ }} – 3,{\rm{ }} – 5,{\rm{ }} – 7,{\rm{ }} \ldots [/latex]
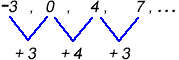
Sequence B : [latex] – 3,{\rm{ }}0,{\rm{ }}4,{\rm{ }}7,{\rm{ }} \ldots [/latex]
Answer
Solution:
Sequence A is an arithmetic sequence since every pair of consecutive terms has a common difference of [latex]-2[/latex], that is, [latex]d=-2[/latex].
On the other hand, sequence B is not an arithmetic sequence. There’s no common difference among the pairs of consecutive terms in the sequence.
2) Find the next term in the sequence below.
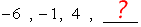
Answer
Solution:
The sequence has a common difference of [latex]5[/latex]. To get to the next term, add the previous term by [latex]5[/latex]. For example, from [latex]4[/latex] to [latex]9[/latex], you add [latex]5[/latex] to [latex]4[/latex] to get to [latex]9[/latex]. That is, [latex]4 + 5 = 9[/latex].
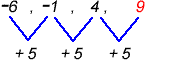
3) Find the next two terms in the sequence below.
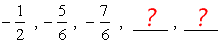
Answer
Solution:
The common difference among adjacent terms is [latex]\large- {1 \over 3}[/latex] . Use this value to get the two succeeding terms. Make sure that you correctly add or subtract fractions with different denominators. If you need a refresher lesson on that, check it out.
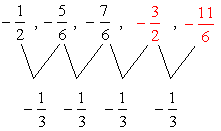
4) If a sequence has a first term of [latex]{a_1} = 12[/latex] and a common difference [latex]d=-7[/latex]. Write the formula that describes this sequence. Use the formula of the arithmetic sequence.

Answer
Solution:
Since we know the values of the first term, [latex]{a_1} = 12[/latex], and the common difference, [latex]d=-7[/latex], the only thing we need to do is substitute these values in the formula.
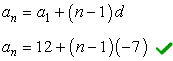
Or, you may further simplify your answer by getting rid of the parenthesis and combining like terms. Both solutions should be acceptable. If you’re not sure, ask your teacher.
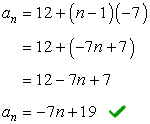
5) Write the formula describing the sequence [latex]6,{\rm{ }}14,{\rm{ }}22,{\rm{ }}30,{\rm{ }}…[/latex]
Answer
Solution:
The first term is [latex]6[/latex], which means [latex]{a_1} = 6[/latex]. The common difference is [latex]d=8[/latex].
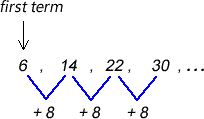
Substitute these values to arrive at the required formula:
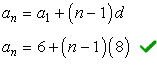
or in a more simplified form;
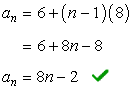
6) Find the 45th term of the arithmetic sequence [latex] – \,9,{\rm{ }} – 2,{\rm{ }}5,{\rm{ }}12,{\rm{ }}…[/latex]
Answer
Solution:
Find the rule that defines the sequence using the arithmetic sequence formula. The first term is [latex]{a_1} = -9[/latex] while the common difference is [latex]d=7[/latex].
Plug these values in the formula, we get
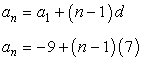
Now we can find the 45th term,
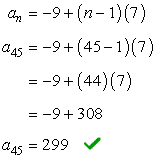
7) Write the formula of a sequence with two given terms, [latex]{a_5} = -32[/latex], and [latex]{a_{18}} = 85[/latex].
Answer
Solution:
Use the information of each term to construct an equation with two unknowns using the arithmetic sequence formula.
- For [latex]{a_5} = -32[/latex]
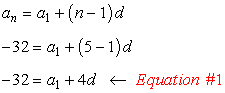
- For [latex]{a_{18}} = 85[/latex]
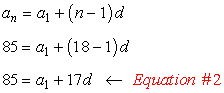
Solve the system of equations using the Elimination Method. Multiply Equation # 1 by [latex]−1[/latex] and add it to Equation #2 to eliminate [latex]{a_1}[/latex].

After finding the value of the common difference, it is now easy to find the value of the first term. Back substitute [latex]d=9[/latex] to any of the two equations to find [latex]{a_1}[/latex].
We’ll use Equation #1 for this,
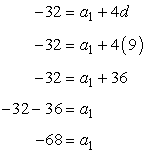
Since [latex]{a_1} = -68[/latex] and [latex]d=9[/latex], the formula we’re looking for is,
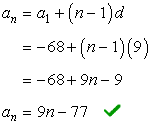
You may also be interested in these related math lessons or tutorials:
