Arithmetic Series Formula
The word series implies sum. We can transform a given arithmetic sequence into an arithmetic series by adding the terms of the sequence. The example below highlights the difference between the two.
Sequence versus Series
Arithmetic Sequence (list):
[latex]\large{2,4,6,8,10,…}[/latex]
Arithmetic Series (sum):
[latex]\large{2 + 4 + 6 + 8 + 10…}[/latex]
Notice that in a sequence, we list the terms separated by commas while in a series, the terms are added as indicated by the plus symbols.
Therefore, an arithmetic series is simply the sum of the terms of an arithmetic sequence. More specifically, the sum of the first [latex]\large\color{red}{n}[/latex] terms in an arithmetic sequence is called the partial sum. The partial sum is denoted by the symbol [latex]\large{{S_n}}[/latex].
Below is the general form of the arithmetic series formula. This works best if the first and the last terms are given in the problem.

Notes:
▶︎ The Arithmetic Series Formula is also known as the Partial Sum Formula.
▶︎ The Partial Sum Formula can be described in words as the product of the average of the first and the last terms and the total number of terms in the sum.
▶︎ The Arithmetic Sequence Formula is incorporated/embedded in the Partial Sum Formula. It is in fact the nth term or the last term [latex]\large\color{blue}{a_n}[/latex] in the formula.
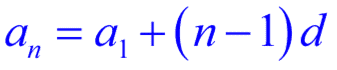
▶︎ Become familiar with both the arithmetic series formula and the arithmetic sequence formula (nth term formula) because they go hand in hand when solving many problems.
[latex]\Large{{S_n} = n\left( {{{{a_1} + \,{a_n}} \over 2}} \right)}[/latex]
and
[latex]\large{{a_n} = {a_1} + \left( {n – 1} \right)d}[/latex]
Before we start working with examples, you may recall me mentioning that the arithmetic sequence formula is embedded in the arithmetic series formula. If we substitute and expand the nth term formula within the partial sum formula, what we will get is a new and useful form of the arithmetic series formula.
Below is the alternative formula for the arithmetic series. Consider this if the last term is not given.
Alternative Arithmetic Series Formula
![Sn=n/2[2a1+(n-1)d]](https://www.chilimath.com/wp-content/uploads/2021/01/alternative-formula-of-arithmetic-series.png)
where:
[latex]\large{{a_1}}[/latex] is the first term
[latex]\large{{d}}[/latex] is the common difference
[latex]\large{{n}}[/latex] is the number of terms in the sum
Examples of Applying the Arithmetic Series Formula
Example 1: Find the sum of the first [latex]100[/latex] natural numbers.
This is an easy problem. The purpose of this problem is to serve as an introductory example. This should help you get familiar quickly with the arithmetic series formula. Once you have a basic understanding of how to use the formula, you should be able to tackle more demanding problems as you will see later in this lesson.
Recall that the natural numbers are the counting numbers. We can write the finite arithmetic sequence as
[latex]1,2,3,4,…,100[/latex]
and its related arithmetic series as
[latex]1 + 2 + 3 + 4 + … + 100[/latex]
Clearly, the first term is [latex]1[/latex], the last term is [latex]100[/latex], and the number of terms being added is also [latex]100[/latex].
Substitute the values into the formula then simplify to get the sum.
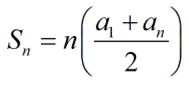
Since [latex]{a_1} = 1[/latex], [latex]{a_{100}} = 100[/latex], and [latex]n = 100[/latex] we have
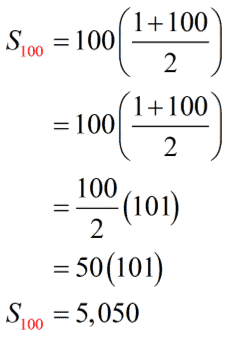
Thus, the sum of the first [latex]100[/latex] natural or counting numbers is [latex]5,050[/latex].
If you want to practice more in finding the sum of the first [latex]200[/latex], [latex]300[/latex], [latex]400[/latex], and [latex]500[/latex] natural numbers, you can use the list of partial sums of natural numbers up to 1,000 that I created as an answer key.
Example 2: Find the partial sum of the given arithmetic series.
[latex]\large{7 + 12 + 17 + 22 + … + 187}[/latex]
If this is your first time solving this type of problem, you may find this a bit overwhelming. Not that it is difficult but because the values that you need are not explicitly given. This can throw you off because you don’t even know how to get started. However, if you have a strategy from the beginning you will realize this problem is not that bad.
What we need to do is to examine the given series. Identify the values that are pertinent and useful to us. Sometimes by doing it this way, the next logical step will be revealed to us.
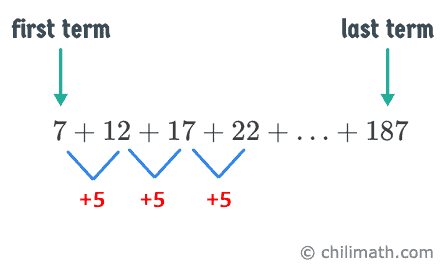
So this is the information we gathered from the series. The first term is [latex]7[/latex]. Since [latex]12-7=5[/latex], [latex]17-12=5[/latex], and [latex]22-17=5[/latex], then the common difference is [latex]5[/latex]. The last term is [latex]187[/latex]. That means the number of terms [latex]\large\color{red}n[/latex] being added in the series is missing.
[latex]\large{a_1} = 7[/latex]
[latex]\large{d=5}[/latex]
[latex]\large{a_n} = 187[/latex]
[latex]\large{n = \,?}[/latex]
I hope at this time, you can agree with me that we have no other option but to use the nth term formula to find [latex]\large\color{red}n[/latex]. Once we find the value for [latex]\large{n}[/latex], we will substitute that into the arithmetic series formula together with the first and last terms to find the sum of the given arithmetic series.

Now, let’s find [latex]\large{n}[/latex] using the nth term formula.
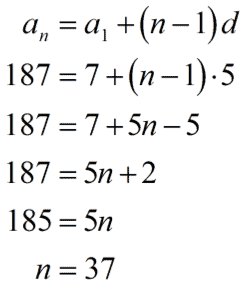
Finally, we have all the values that we need to calculate the sum of the given series which are [latex]\large{n=37}[/latex], [latex]\large{a_1} = 7[/latex], and [latex]\large{a_n} = 187[/latex].
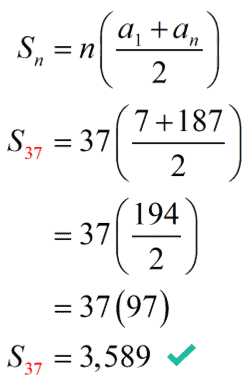
Example 3: Find the sum of the first [latex]\large{51}[/latex] terms of the arithmetic sequence.
[latex]\large{12\,,\,19\,,\,26\,,\,33\,,…}[/latex]
The strategy here is similar to Example 2. Instead of finding the number of terms [latex]\large\color{red}n[/latex], we will use the nth term formula to find the [latex]51[/latex]st term. Then, we use the arithmetic series formula to calculate the sum of the first [latex]51[/latex] terms of the sequence.
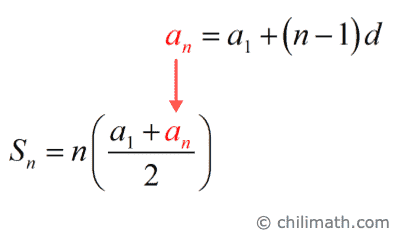
So what value can we extract from the given problem?
Well, the number of terms [latex]\large\color{red}n[/latex] to be added is explicitly given in the problem which is [latex]n=51[/latex].
Now, from the arithmetic sequence, the first term and common difference are easily identifiable. The first term is obviously [latex]12[/latex] while the common difference is [latex]7[/latex] since [latex]19 – 12 = 7[/latex], [latex]26 – 19 = 7[/latex], and [latex]33 – 26 = 7[/latex].

So here is the information we have gathered. It means the nth term is what we are looking for.
[latex]\large{a_1}=12[/latex]
[latex]\large{n=51}[/latex]
[latex]\large{d=7}[/latex]
[latex]\large{a_n}=\,?[/latex]
Plug in the values into the nth term formula then simplify to get the [latex]51[/latex]st term.
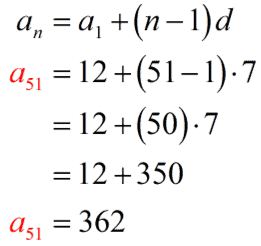
We can finally find the sum of the first [latex]51[/latex] terms because we know the number of terms [latex]n=51[/latex], the first term [latex]{a_1}=7[/latex], and the last term [latex]{a_n}=362[/latex].
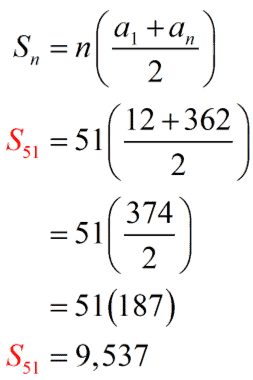
Example 4: The 10th term of an arithmetic sequence is [latex]17[/latex] and the 30th term is [latex]-63[/latex]. What is the 50th partial sum [latex]\large{S_{50}}[/latex] of the arithmetic sequence?
Here’s the big picture. In order to find the 50th partial sum, we will need to know the first term [latex]\large{a_1}[/latex], and the last term [latex]\large{a_n}[/latex] which is the same as the 50th term. Obviously, there will be 50 terms in the series because we are summing up the terms from the first up to the 50th term.
To find the first term [latex]\large{a_1}[/latex], we will use the nth term formula together with the given information in the problem to generate a system of equations where the unknown variables are the first term [latex]\large{a_1}[/latex] and the common difference [latex]d[/latex].
[latex]\large{{a_n} = {a_1} + \left( {n – 1} \right)d}[/latex]
Therefore, we have
- 10th term is [latex]17[/latex]
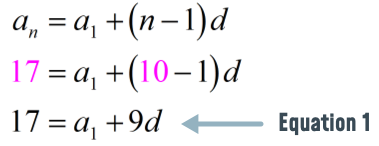
- 30th term is [latex]-63[/latex]
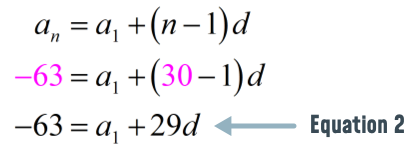
Now, this is the system of equations that we are going to solve. We can find the values of the first term [latex]\large{a_1}[/latex] and the common difference [latex]\large{d}[/latex].
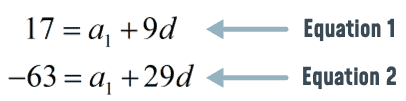
We will solve this system of equations using the Elimination Method. We subtract equation #2 from equation #1 to get rid of [latex]\large{a_1}[/latex], thus isolating [latex]\large{d}[/latex].
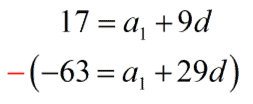
This gives us
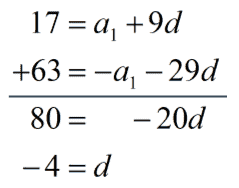
Since we already know the value of the common difference [latex]\large{d}[/latex], we can easily solve for the first term [latex]\large{a_1}[/latex]. Choose any of the two equations, equation #1 or equation #2, substitute the value of [latex]\large{d}[/latex] then solve for [latex]\large{a_1}[/latex]. We will choose equation #1 because it is a much simpler equation to deal with.
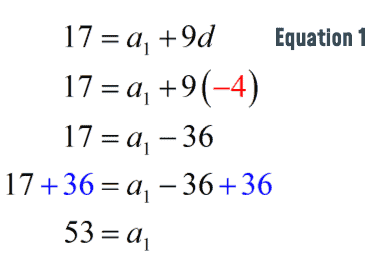
By knowing the first term, and the common difference of a sequence, we can put together the formula that can determine any term in the sequence.
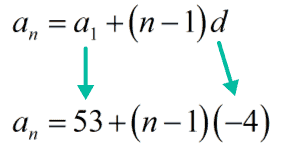
Using the formula that we have come up with, we can now find the 50th term [latex]\large{{a_{50}}}[/latex] in the sequence.
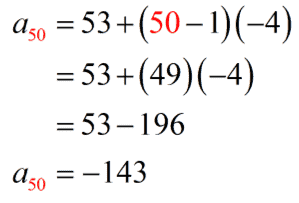
Finally, we have all that we need to compute for the 50th partial sum using the arithmetic series formula.

Substitute the values into the formula then simplify.
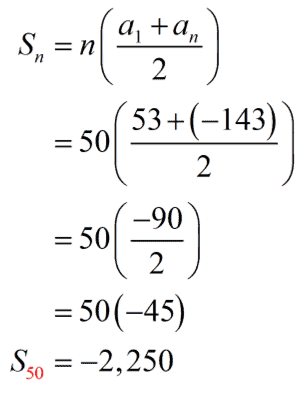
Example 5: The 10th term of an arithmetic sequence is [latex]23[/latex] while its 12th partial sum is [latex]192[/latex]. Find the sum of the first [latex]40[/latex] terms of the sequence.
To find the first [latex]40[/latex] terms of the arithmetic sequence, we will use the main arithmetic series formula. However, we need to supply the missing values in the formula, namely the first term [latex]\large{{{a_1}}}[/latex] and the last term [latex]\large{{{a_n}}}[/latex]. The number of terms to be added [latex]\large{n}[/latex] is already given which is [latex]40[/latex].
![Sn = n[{a1+an)/2]](https://www.chilimath.com/wp-content/uploads/2021/02/example-5-big-picture.png)
Now, let’s construct a system of equations wherein the unknown variables are the first term [latex]\large{a{}_1}[/latex] and the common difference [latex]\large{d}[/latex].
The first equation comes from the given information that [latex]\large{{a_{10}} = 23}[/latex]. Plug the values into the nth term formula.
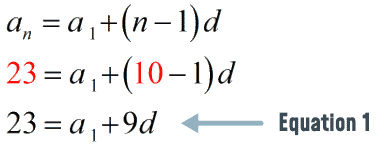
The second equation comes from the given information that [latex]\large{{S_{12}} = 192}[/latex]. Plug the values into the alternative arithmetic series formula.
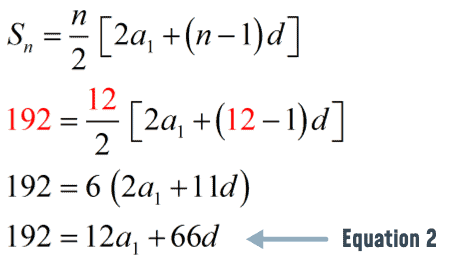
This is the system of equations that we are going to solve by the Elimination Method.
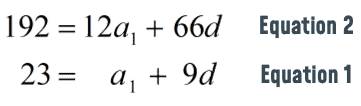
Multiply equation #1 by [latex]-12[/latex].
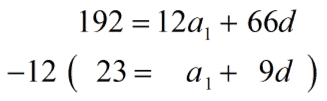
Then add it to equation #2. We get [latex]{d=2}[/latex].
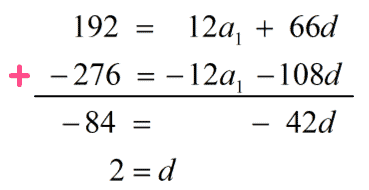
After solving for the value of [latex]\large{d}[/latex], we can now solve for the value of [latex]\large{a{}_1}[/latex]. Pick any of the two equations, substitute the value of [latex]\large{d}[/latex] then solve for [latex]\large{a{}_1}[/latex]. We will use equation #1 because it is a simpler equation.
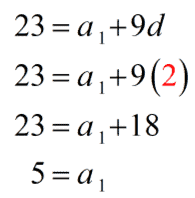
Since we know already the values of [latex]\large{a{}_1}[/latex] and [latex]\large{d}[/latex], we are now ready to write the general term of the sequence which can find any term in the sequence.

To find the 40th term, we have
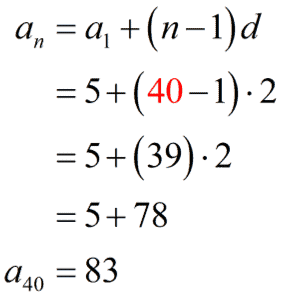
Finally, we have all the required values as shown below to calculate the 40th partial sum.
[latex]\large{n=40}[/latex]
[latex]\large{{a_1} = 5}[/latex]
[latex]\large{{{a_n} = 83}}[/latex]
Plug in the values into the arithmetic series formula then simplify.
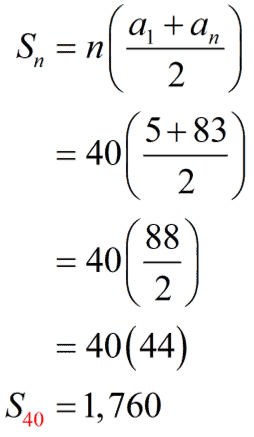
You may also be interested in these related math lessons or tutorials:
Derivation of the Arithmetic Series Formula
Arithmetic Series Formula Practice Problems
