Infinite Geometric Series Formula
In the previous lesson, we discussed how to find the sum of a finite geometric sequence. It is considered finite because we were summing up a fixed number of terms. That means, finite sequence has a first and last term. On the other hand, infinite geometric series deals with a sequence that keeps on going forever without end. In other words, the number of terms in the sequence is infinite. The terms in an infinite series looks like this.
[latex]{a_1} + {a_1}r + {a_1}{r^2} + {a_1}{r^3} + ….[/latex]
The first term is [latex]a_1[/latex], the second term is [latex]{a_1}r[/latex], the third term is [latex]{a_1}{r^2}[/latex], and so on. The terms keep coming and they will never run out. The [latex]r[/latex] is called the common ratio. That is the number that we always get if we divide every term by the previous term.
If we are adding infinite terms, two things could happen. If we keep adding the terms more and more, the sum is either getting smaller and smaller (becoming more negative), or larger and larger (becoming more positive), we say that it diverges. The series diverges because the sum doesn’t approach or get to a finite limit. However, if the sum is getting closer and closer to a particular fixed value, we say that the series converges.
How do we know if a series converges or diverges? There is a simple way to know. Just look at the common ratio, [latex]r[/latex]. If the absolute value of the common ratio is less than [latex]1[/latex] that is [latex]\left| r \right| < 1[/latex], then the series converges. If the absolute value of the common ratio is greater than [latex]1[/latex], that is [latex]\left| r \right| > 1[/latex], then the series diverges.
Here’s the formula for the infinite geometric series:
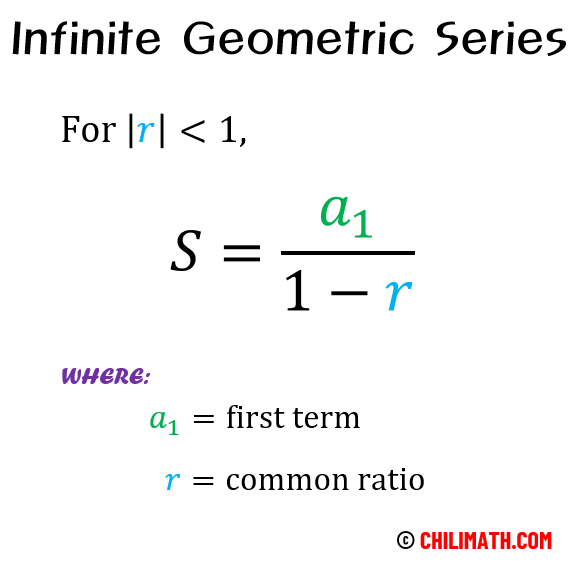
I just want to reiterate that for the formula to work, the value of the common ratio [latex]r[/latex] must be between [latex]-1[/latex] and [latex]1[/latex], or a fraction with an absolute value less than [latex]1[/latex].
Let’s take a look at some examples!
Example 1: Find the sum of the infinite geometric series.
[latex]\Large1 + {1 \over 3} + {1 \over 9} + {1 \over {27}} + …[/latex]
The first thing we need to do is verify if the sequence is geometric. Divide each term by the preceding term. If the quotient is the same every time we divide, then we have a geometric sequence.
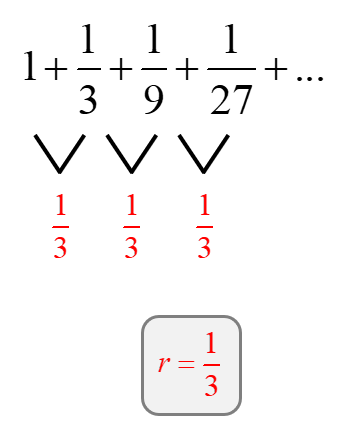
As you can see, there’s a common ratio of [latex]\large{1 \over 3}[/latex] which means it is a geometric series.
Now that we know we are dealing with a geometric sequence, it’s time for us to figure out if the related series can be summed up to a finite limit.
The only test that we have to perform is check if the common ratio [latex]r[/latex] has an absolute value of less than [latex]1[/latex].
Since [latex]\large\left| r \right| = {1 \over 3} < 1[/latex], it implies that the series converges thus we can use the infinite geometric series formula to find the finite sum.
From the problem, the first term is [latex]{a_1} = 1[/latex] and and the common ratio is [latex]\large{r = {1 \over 3}}[/latex]. Let’s plug these values in the formula and simplify.
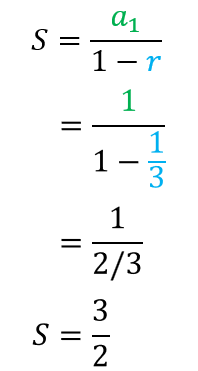
Therefore, the sum of the infinite geometric series is [latex]\large{3 \over 2}[/latex].
Example 2: Find the sum of the infinite geometric series.
[latex]\large2 + {4 \over 3} + {8 \over 9} + {{16} \over {27}} + …[/latex]
First, verify if the series is geometric by dividing each term by the previous one. Does it yield the same quotient?
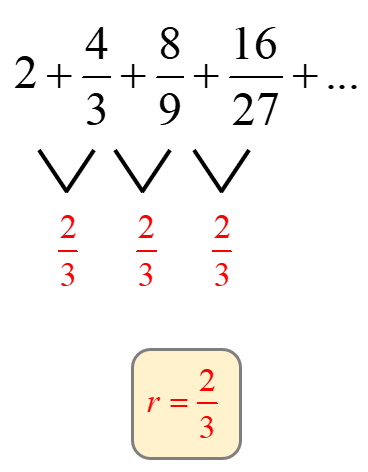
Yes, it does! The common ratio is [latex]\large{r = {2 \over 3}}[/latex].
Since [latex]\large\left| r \right| = {2 \over 3} < 1[/latex], that means the series converges, and therefore we can use the formula to find the finite sum.
We know [latex]a_1=2[/latex] and [latex]\large{r = {2 \over 3}}[/latex]. Substitute these values in the formula then simplify.
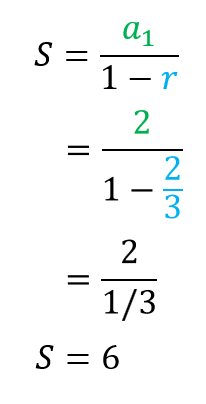
Therefore, the sum of the infinite geometric series is [latex]6[/latex].
Sometimes, an infinite geometric series may be written in a compact form, using the sigma notation [latex]\sum [/latex] that looks like a weird capital letter E. This notation signifies summation in math.
As previously stated, an infinite geometric series only converges if the value of the common ratio [latex]r[/latex] is between [latex]-1[/latex] and [latex]1[/latex]. That means, the absolute value of [latex]r[/latex] is less than [latex]1[/latex]. In sigma notation form, the common ratio is usually wrapped around by a parenthesis and being raised to a power.

Example 3: Find the sum of the infinite geometric series, if possible.
[latex]\large\sum\limits_{n = 1}^\infty {5{{\left( {{3 \over 2}} \right)}^{n – 1}}} [/latex]
The common ratio is the number inside the parenthesis which is [latex]\large{{3 \over 2}}[/latex]. Since the absolute value of [latex]r[/latex] is NOT less than [latex]1[/latex], that means [latex]\left| r \right| = {3 \over 2} > 1[/latex], this infinite geometric series will not converge which means it will diverge. Therefore, the infinite geometric series won’t have a fixed sum. There’s no need to use the formula. Just a word of caution, if you proceed to use the formula to find the sum, you will still get an answer but your sum is incorrect.
Example 4: Find the sum of the infinite geometric series, if possible.
[latex]\large\sum\limits_{n = 1}^\infty {8{{\left( { – {3 \over 4}} \right)}^{n – 1}}} [/latex]
The absolute value of the common ratio is less than [latex]1[/latex] which means the series converges.
[latex]\large\left| r \right| = \left| { – {3 \over 4}} \right| = {3 \over 4} < 1[/latex]
Let’s use the formula to find the sum.
The first term is [latex]{a_1} = 8[/latex] and the common ratio is [latex]\large{r = – {3 \over 4}}[/latex].
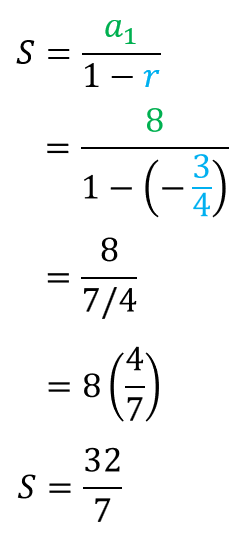
Therefore, the sum of the infinite geometric series is [latex]\large{{32} \over 7}[/latex].
Example 5: Find the sum of the infinite geometric series, if possible.
[latex]\large\sum\limits_{n = 1}^\infty {4{{\left( {0.3} \right)}^{n – 1}}} [/latex]
The absolute value of the common ratio is less than [latex]1[/latex]. It means the series converges and therefore we can find the sum.
[latex]\left| r \right| = 0.3 < 1[/latex]
The first term is [latex]4[/latex] and the common ratio is [latex]0.3[/latex]. The common ratio can be expressed in fraction form as [latex]\large{3 \over {10}}[/latex].
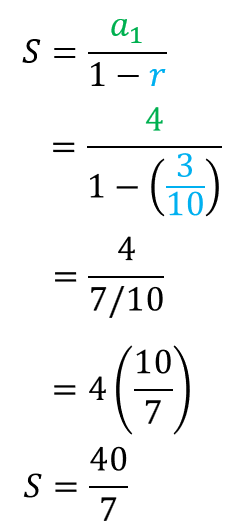
Therefore, the sum of the infinite geometric series is [latex]\large{{40} \over 7}[/latex]
Example 6: Write the repeating decimal as a fraction.
[latex]0.7777…[/latex]
Notice that we can rewrite this repeating decimal as an infinite series.
[latex]0.7777… = 0.7 + 0.07 + 0.007 + …[/latex]
Is the infinite series geometric? Let’s divide each term by the previous one and check if we get a common ratio.
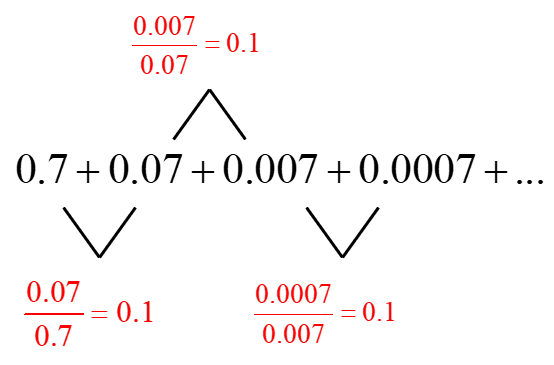
Yes, the common ratio is [latex]0.1[/latex]. So this is an infinite geometric series. That means we can use the formula to find the finite sum.
The first term is [latex]{a_1} = 0.7[/latex] and the common ratio is [latex]r = 0.1[/latex].
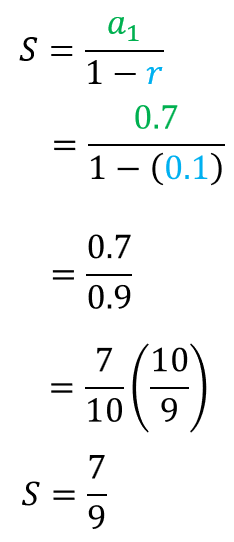
Therefore, [latex]0.7777…[/latex] can be written as [latex]\large{7 \over 9}[/latex].
You may also be interested in these related math lessons or tutorials:
