Geometric Sequence Formula
A geometric sequence (also known as geometric progression) is a type of sequence wherein every term except the first term is generated by multiplying the previous term by a fixed nonzero number called common ratio, r.
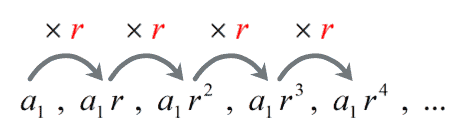
More so, if we take any term in the geometric sequence except the first term and divide it by the previous term, the quotient is always the same. This constant or fixed quotient is called the common ratio and is usually represented by the letter r.
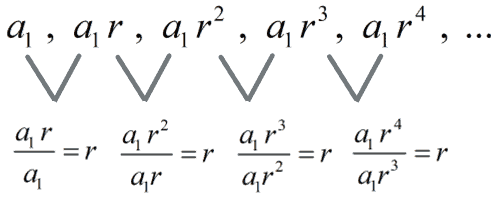
How to “Derive” the Geometric Sequence Formula
To generate a geometric sequence, we start by writing the first term. Then we multiply the first term by a fixed nonzero number to get the second term of the geometric sequence.
To obtain the third sequence, we take the second term and multiply it by the common ratio. Maybe you are seeing the pattern now. To get to the next term of the sequence, you multiply the preceding term by the constant nonzero number that we used as the common multiplier.
To make a sense of this all, let’s have a concrete example. Suppose we have a geometric sequence wherein
the first term, [latex]\large{a_1}[/latex], is 3
and
the fixed constant or common ratio, [latex]\large{r}[/latex], is 2.
So if the first term is [latex]3[/latex] then we have
[latex]\large{{a_1} = 3}[/latex]
The second term is generated by multiplying the first term by the fixed constant [latex]2[/latex].
[latex]\large{{a_2} = 3\left( 2 \right)^1}[/latex]
The third term is generated by multiplying the second term by the fixed constant [latex]2[/latex].
[latex]\large{{a_3} = 3\left( 2 \right)\left( 2 \right) = 3{\left( 2 \right)^2}}[/latex]
The fourth term is obtained by multiplying the third term by the fixed constant [latex]2[/latex].
[latex]\large{{a_4} = 3\left( 2 \right)\left( 2 \right)\left( 2 \right) = 3{\left( 2 \right)^3}}[/latex]
The fifth term is obtained by multiplying the fourth term by the fixed constant [latex]2[/latex].
[latex]\large{{a_5} = 3\left( 2 \right)\left( 2 \right)\left( 2 \right)\left( 2 \right) = 3{\left( 2 \right)^4}}[/latex]
So now how can we interpret and use the example above to convert it into a formula? Observe that the first term [latex]\color{red}\large{{a_1}}[/latex] is always present in every term of the sequence. In the same manner, the fixed constant [latex]\color{red}\large{r}[/latex] is also attached in every term to some power. Notice that
- if [latex]\large{n}[/latex] is [latex]1[/latex] the power of [latex]\large{r}[/latex] is [latex]0[/latex]
- if [latex]\large{n}[/latex] is [latex]2[/latex] the power of [latex]\large{r}[/latex] is [latex]1[/latex]
- if [latex]\large{n}[/latex] is [latex]3[/latex] the power of [latex]\large{r}[/latex] is [latex]2[/latex]
- if [latex]\large{n}[/latex] is [latex]4[/latex] the power of [latex]\large{r}[/latex] is [latex]3[/latex]
- if [latex]\large{n}[/latex] is [latex]5[/latex] the power of [latex]\large{r}[/latex] is [latex]4[/latex]
Note: [latex]\large{n}[/latex] is the subscript of [latex]\large{a}[/latex] as in [latex]\large{a_n}[/latex]
It means that the power of the fixed constant (also known as the common ratio) [latex]\color{red}\large{r}[/latex] is [latex]1[/latex] less than whatever [latex]\large{n}[/latex] is.
Therefore, we can now deduce that the nth term [latex]\color{red}\large{{a_n}}[/latex] of a geometrc sequence is equal to the first term [latex]\color{red}\large{{a_1}}[/latex] multiplied to the fixed constant (also known as the common ratio) [latex]\color{red}\large{{r}}[/latex] raised to 1 less than [latex]\large{{n}}[/latex].
[latex]\LARGE{{a_n} = {a_1}{\left( r \right)^{n – 1}}}[/latex]
Below is a quick illustration on how we derive the geometric sequence formula.
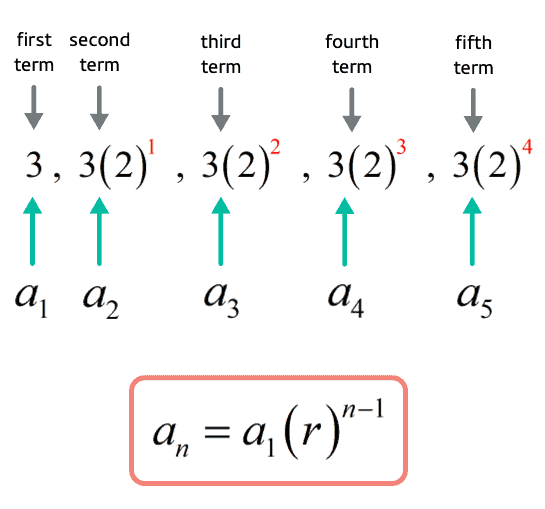
Breakdown of the Geometric Sequence Formula

Notes about the geometric sequence formula:
- the common ratio r cannot be zero
- n is the position of the term in the sequence. For example, the third term is [latex]n=3[/latex], the fourth term is [latex]n=4[/latex], the fifth term is [latex]n=5[/latex], and so on.
Examples of Using the Geometric Sequence Formula
To learn and get familiar with the formula quickly, we will start with easy or foundational problems then gradually progress to more challenging ones. Feel free to skip the problems that you already know and jump to the ones that you want to go over.
Example 1: Tell whether each sequence is geometric or not. Explain.
a) Sequence A: [latex]3,12,48,192,…[/latex]
b) Sequence B: [latex] – 1,2, – 4,8,…[/latex]
c) Sequence C: [latex]4,8,12,16,…[/latex]
d) Sequence D: [latex]\Large{{1 \over 3},{1 \over 2},{3 \over 4},{9 \over 8},…}[/latex]
Solution:
a) Yes. Sequence A is a geometric sequence because there is a common ratio between consecutive terms. The common ratio is [latex]4[/latex].
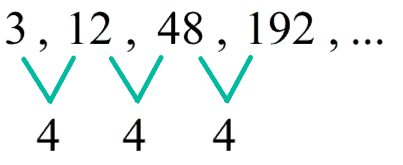
b) Yes. Sequence B is also a geometric sequence since the adjacent terms have a common ratio which is [latex]-2[/latex].
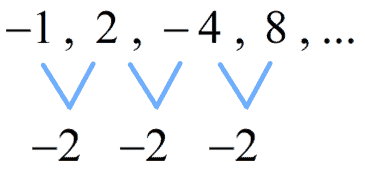
Notice that when a geometric sequence has a negative common ratio, the sequence will have alternating signs. That means the signs of the terms are switching back and forth between positive and negative.
c) No. Sequence C is not a geometric sequence. The consecutive terms don’t have a common ratio.
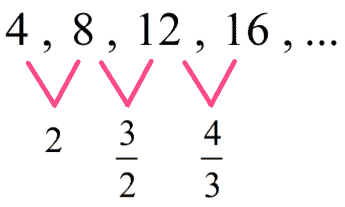
I hope you recognize that this is another kind of sequence. Notice, there is a common difference between consecutive terms which is [latex]4[/latex]. That is,
[latex]8-4=4[/latex]
[latex]12-8=4[/latex]
[latex]16-12=4[/latex]
Since the common difference is [latex]4[/latex], this is in fact an arithmetic sequence.
d) Yes. Sequence D is a geometric sequence because it has a common ratio of [latex]\Large{{3 \over 2}}[/latex].
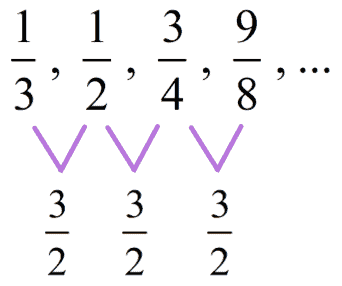
Remember that when we divide fractions, we convert the problem from division to multiplication. Take the dividend (fraction being divided) and multiply it to the reciprocal of the divisor. Then, we simplify as needed.
[latex]\Large{{1 \over 2} \div {1 \over 3} = {1 \over 2} \times {3 \over 1} = {3 \over 2}}[/latex]
[latex]\Large{{3 \over 4} \div {1 \over 2} = {3 \over 4} \times {2 \over 1} = {3 \over 2}}[/latex]
[latex]\Large{{9 \over 8} \div {3 \over 4} = {9 \over 8} \times {4 \over 3} = {3 \over 2}}[/latex]
Example 2: Write a geometric sequence with five (5) terms wherein the first term is [latex]0.5[/latex] and the common ratio is [latex]6[/latex].
The first term is given to us which is [latex]\large{{a_1} = 0.5}[/latex]. Thus, we will have to find the other four terms. We can use the common ratio to produce the next four terms. The common ratio which in this case is [latex]6[/latex] will serve as the fixed multiplier to calculate the rest of the terms in the sequence.
The first term is [latex]{0.5}[/latex]. The second term is the first term multiplied by the common ratio [latex]6[/latex] which equals [latex]3[/latex]. The third term is the second term times [latex]6[/latex], and so on.
[latex]\large{{a_1} = 0.5}[/latex]
[latex]\large{{a_2} = 0.5\left( 6 \right) = 3}[/latex]
[latex]\large{{a_3} = 3\left( 6 \right) = 18}[/latex]
[latex]\large{{a_4} = 18\left( 6 \right) = 108}[/latex]
[latex]\large{{a_5} = 108\left( 6 \right) = 648}[/latex]
Therefore, the geometric sequence that satisfies the given conditions is
[latex]{0.5\,\,,\,\,3\,\,,\,\,18\,\,,\,\,\,108\,\,,\,\,648\,\,,\,\,…}[/latex]
Example 3: Generate a geometric sequence with five (5) terms such that each term is half the previous term. Answers may vary.
There is an infinite number of geometric sequences that can satisfy this condition because we are not restricted to a particular first term. We can use any numbers as our first term. That’s why the answers to this problem will vary as we are free to choose our starting term.
The problem can be expressed algebraically as
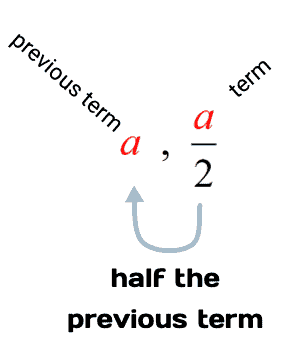
OR
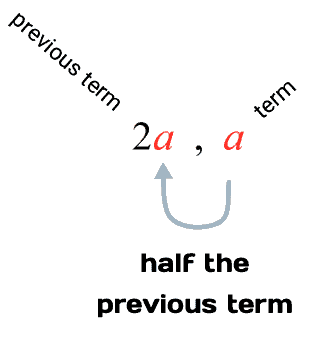
It only means that to go from the previous term to the following term, we multiply the previous term by [latex]\Large{{1 \over 2}}[/latex] to get to the next.
If we pick [latex]48[/latex] as our first term, we multiply it by [latex]\Large{{1 \over 2}}[/latex] to produce the second term. To generate the third term, multiply the second term by [latex]\Large{{1 \over 2}}[/latex], and so on.
[latex]\large{{a_1} = 48}[/latex]
[latex]\large{{a_2} = 48\left( {{1 \over 2}} \right) = 24}[/latex]
[latex]\large{{a_3} = 24\left( {{1 \over 2}} \right) = 12}[/latex]
[latex]\large{{a_4} = 12\left( {{1 \over 2}} \right) = 6}[/latex]
[latex]\large{{a_5} = 6\left( {{1 \over 2}} \right) = 3}[/latex]
So here’s our geometric sequence with five (5) terms such that each term (except the first term) is one-half of the previous term.
[latex]\large{48\,,\,\,24\,\,,\,\,12\,\,,\,\,6\,\,,\,\,3\,\,,\,\,…}[/latex]
Example 4: The first term of the geometric sequence is [latex]7[/latex] while its common ratio is [latex]-2[/latex]. Write the nth term formula of the sequence in the standard form.
The standard formula of the geometric sequence is

This is an easy problem because the values of the first term and the common ratio are given to us. We simply substitute them into the formula and we are done.
Since [latex]{a_1} = 7[/latex] and [latex]r = – 2[/latex], we have
[latex]\large{{a_n} = 7{\left( { – 2} \right)^{n – 1}}}[/latex]
Example 5: Determine the nth term formula of the geometric sequence below.
[latex]\large{16\,,\,\,12\,\,,\,\,9\,\,,\,\,…}[/latex]
To write the nth term formula, we will need the values of the first term and the common ratio. Since we are given the geometric sequence itself, the first term [latex]\large{{a_1}}[/latex] can easily be found.
The first term of the geometric sequence is obviously [latex]16[/latex].

Divide each term by the previous term. Since the quotients are the same, then it becomes our common ratio. In this case, we have [latex]\Large{r = {3 \over 4}}[/latex].
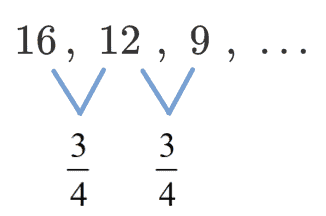
Substituting the values of the first term and the common ratio into the formula, we get
[latex]\Large{{a_n} = {a_1}{\left( r \right)^{n – 1}}}[/latex]
[latex]\Large{{a_n} = 16{\left( {{3 \over 4}} \right)^{n – 1}}}[/latex]
Example 6: Determine the indicated terms below using the geometric sequence formula.
a) The first term is [latex]3[/latex]. Find the sixth term if the common ratio is [latex]2[/latex].
b) The first term is [latex]-2[/latex]. Find the seventh term if the common ratio is [latex]-3[/latex].
Solution: These two (2) problems are very similar. The first term and the common ratio are both given in the problem. The only thing we have to do is to plug these values into the geometric sequence formula then use it to find the nth term of the sequence.
a) The first term is [latex]\large{{a_1} = 3}[/latex] while its common ratio is [latex]r = 2[/latex].
This gives us

To find the sixth term, we let [latex]n=6[/latex] then simplify.
[latex]\large{a_n} = 3{\left( 2 \right)^{n – 1}}[/latex]
[latex]\large{a_6} = 3{\left( 2 \right)^{6 – 1}}[/latex]
[latex]\large = 3{\left( 2 \right)^5}[/latex]
[latex]\large = 3\left( {32} \right)[/latex]
[latex]\large{a_6} = 96[/latex]
b) The first term is [latex]\large{{a_1} = -2}[/latex] and the common ratio is [latex]r = -3[/latex].
The nth term formula becomes

To find the seventh term, we will set [latex]n=7[/latex] then simplify.
[latex]\large{a_n} = – 2{\left( { – 3} \right)^{n – 1}}[/latex]
[latex]\large{a_7} = – 2{\left( { – 3} \right)^{7 – 1}}[/latex]
[latex]\large = – 2{\left( { – 3} \right)^6}[/latex]
[latex]\large = – 2\left( {729} \right)[/latex]
[latex]\large {a_7} = – 1,458[/latex]
Example 7: Find the tenth term of the geometric sequence below.
[latex]\Large{1 \over 3}\,\,,\,\,\,1\,\,,\,\,\,3\,\,,\,\,\,9\,\,,\,\,…[/latex]
Solution:
This problem is similar to example 6. The only difference is that the values of the first term and common ratio are not given upfront. However, they can easily be found and computed from the geometric sequence.
The very first term of the sequence is very obvious to identify.

Calculate the common ratio by dividing each term by the previous term. If the quotients are the same, then it is our common ratio.

Since the first term is [latex]\large{a_1} = {1 \over 3}[/latex] and the common ratio is [latex]r = 3[/latex], we write the general formula as
[latex]\Large{a_n} = {1 \over 3}{\left( 3 \right)^{n – 1}}[/latex]
The 10th term is calculated by letting [latex]n=10[/latex].
[latex]\Large{a_{10}} = {1 \over 3}{\left( 3 \right)^{10 – 1}}[/latex]
[latex]\Large = {1 \over 3}{\left( 3 \right)^9}[/latex]
[latex]\large = {1 \over 3}\left( {19,683} \right)[/latex]
[latex]\large {a_{10}} = 6,561[/latex]
Example 8: The second term of a geometric sequence is [latex]2[/latex], and the fifth term is [latex]\Large{1 \over {32}}[/latex]. Find the ninth term.
We will use the given two terms to create a system of equations that we can solve to find the common ratio [latex]r[/latex] and the first term [latex]{a_1}[/latex]. After doing so, it is possible to write the general formula that can find any term in the geometric sequence. In particular, we want to find the ninth term.
Since [latex]\large{a_2} = 2[/latex] and [latex]\large{a_5} = {1 \over {32}}[/latex], we substitute them in the nth term formula [latex]\large{a_n} = {a_1}{\left( r \right)^{n – 1}}[/latex] to get
Equation 1:
[latex]\large2 = {a_1}r[/latex]
Equation 2:
[latex]\Large{{1 \over {32}} = {a_1}{r^4}}[/latex]
Let’s divide equation 2 by equation 1 to cancel the variable [latex]\large{a_1}[/latex]. What’s left is an equation that we can solve for [latex]\large{r}[/latex].
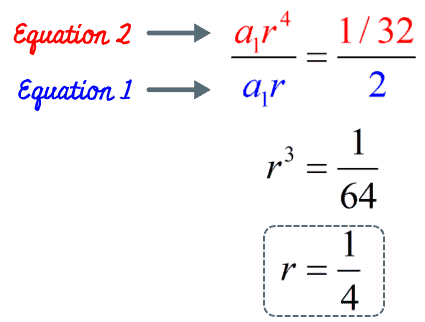
We can now solve for the value of the first term by substituting the value of [latex]r[/latex] to either equation 1 or 2 then solve for [latex]\large{a_1}[/latex]. We will use equation 1 because it is much simpler.
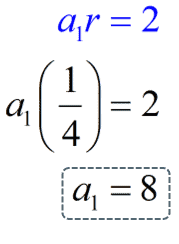
This gives us the nth term formula of the geometric sequence.

Finally, we can solve for the 9th term of the geometric sequence by letting [latex]n=9[/latex] and simplifying it.
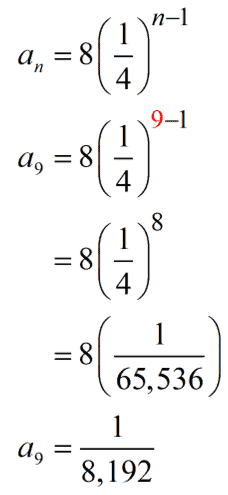
Example 9: The third term of a geometric sequence is [latex]5[/latex], and the seventh term is [latex]\Large{5 \over {16}}[/latex]. Find the thirteenth term.
I’m sure that you already know the drill. We will use the information of the given two terms from the problem to create a system of equations with [latex]\color{red}\large{a_1}[/latex] and [latex]\color{red}r[/latex] as the unknown variables.
For [latex]\large{a_3=5}[/latex], our equation 1 is
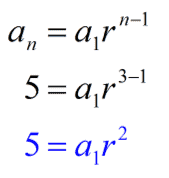
For [latex]\large{a_7} = {5 \over {16}}[/latex], our equation 2 is
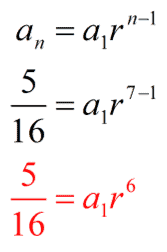
We divide equation 2 by equation 1 to cancel out the [latex]\large{a_1}[/latex] term then solve for [latex]\large{r}[/latex].
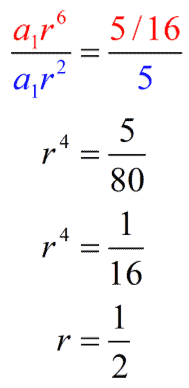
Now, we solve for [latex]\large{a_1}[/latex] by substituting the value of [latex]r=1/2[/latex] to any of the equations. We will use equation 1 because it is the simpler one of the two.
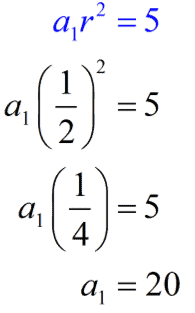
We can now put together the nth term formula of the geometric sequence.
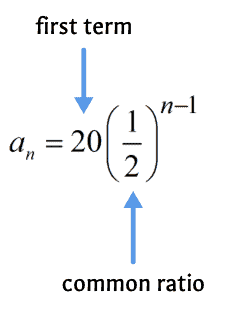
Finally, we solve the value of the missing term. Since we are looking for the 13th term of the geometric sequence, we let [latex]n=13[/latex] then simplify.
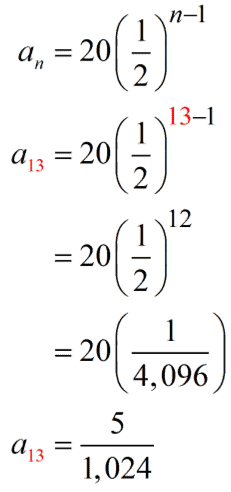
You may also be interested in these related math lessons or tutorials:
Geometric Series Practice Problems
