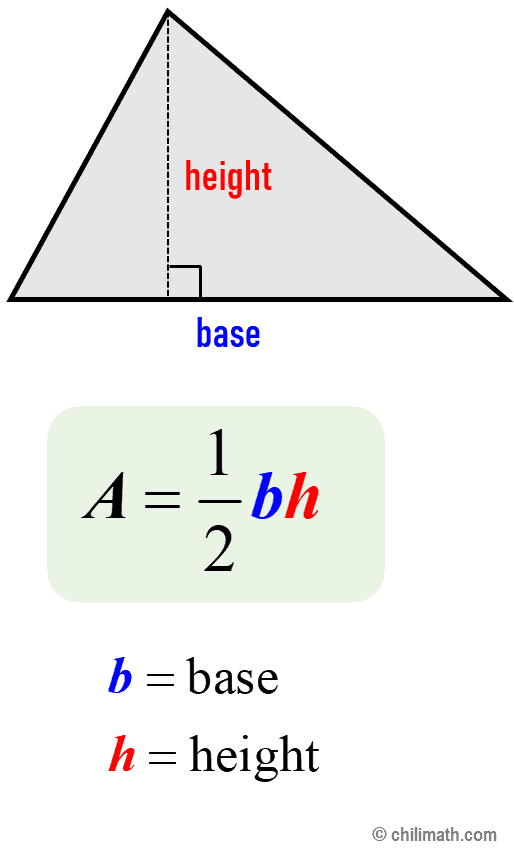
Area of a Triangle Formula
The area of a triangle [latex]A[/latex] is half the product of its base [latex]b[/latex] and its height [latex]h[/latex]. The height of a triangle is also known as the altitude. This formula works only if the base is perpendicular to the height. That means the base and the height form a right angle or [latex]{90^\circ }[/latex] angle.
Examples Involving Area of Triangle Formula
Example 1: Find the area of a triangle with a base of [latex]5[/latex] and a height of [latex]3[/latex].
We have [latex]\color{blue}b=5[/latex] and [latex]\color{red}h=3[/latex]. Plug the values into the formula then simplify.
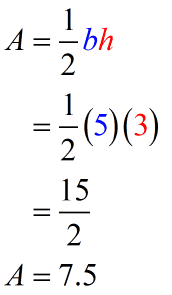
Since the unit of measure is not specified, we can write the final answer as [latex]A = 7.5[/latex] square units.
Example 2: Find the area of triangle ABC.

Clearly, the base is [latex]\color{blue}9[/latex] feet while the height is [latex]\color{red}4[/latex] feet. Observe that the base and height meet at a 90-degree angle. To find the area of the given triangle, we multiply the base and height then divide the product by [latex]2[/latex].
Notice that the height of the triangle is found inside of the triangle.
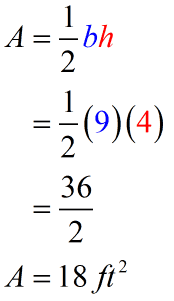
The final answer is [latex]18[/latex] square feet.
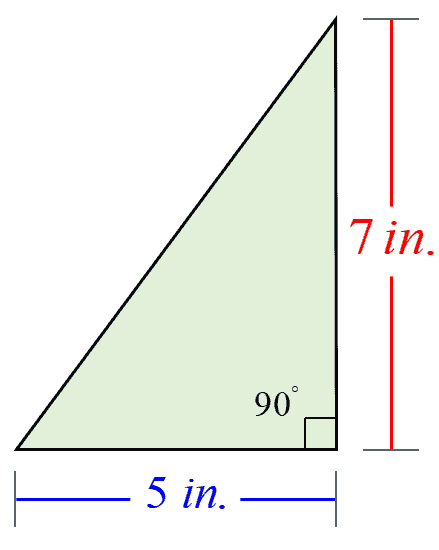
Example 3: Draw a right triangle with legs of length [latex]5[/latex] inches and [latex]7[/latex] inches. Calculate its area.
The legs of a right triangle are the sides that form a right angle, [latex]{90^ \circ }[/latex]. More so, the legs also serve as the height and base of the triangle. If we let the base be the shorter leg, this forces the longer leg to be the height. Thus, we have [latex]\color{blue}b=5[/latex] and [latex]\color{red}h=7[/latex].
Notice that the height is part of the triangle itself, which is one of the two legs. In fact, any of the legs can be designated as height since they intersect at a 90-degree angle.
Calculating the area of the right triangle, we have
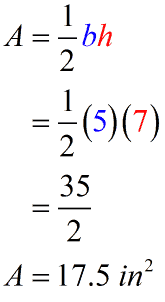
The final answer is [latex]17.5[/latex] square inches.
Example 4: Sketch an obtuse triangle with a base of [latex]4[/latex] centimeters and an exterior height of [latex]4.5[/latex] centimeters. Then, find its area.
An obtuse triangle is a type of triangle wherein one of its interior angles has a measure of greater than 90 degrees but less than 180 degrees.
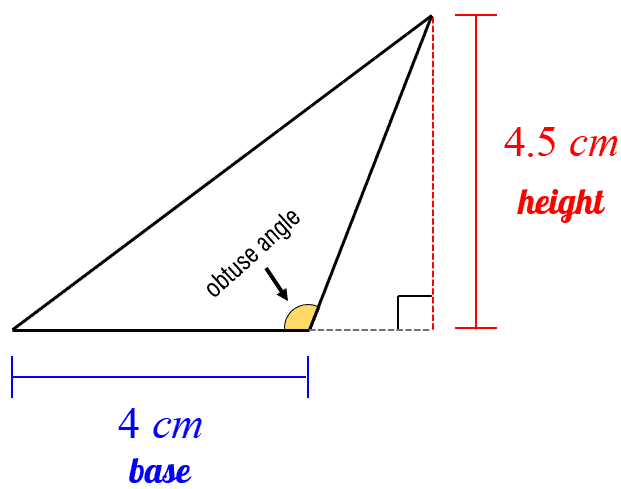
In this scenario, the height of the triangle is formed outside, and to be exact, opposite to one of the acute angles. The height is perpendicular to the extended base.
Since [latex]\color{blue}b=4[/latex] and [latex]\color{red}h=4.5[/latex], the area of the triangle is computed as follows.
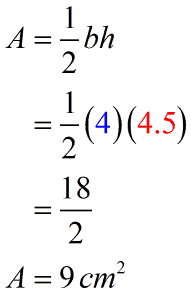
Therefore, the final answer is [latex]9[/latex] square centimeters.
Example 5: What is the area of a triangle whose base is [latex]2.5[/latex] feet and height is [latex]12[/latex] inches?
Before we can apply the formula to find the area, we need to ensure that the units of measure are the same. We can either express the area in terms of square feet [latex]ft^2[/latex] or square inches [latex]in^2[/latex].
To express the area in square feet, we will keep the base of [latex]2.5[/latex] feet but convert the height of [latex]12[/latex] inches into feet. By conversion, [latex]12[/latex] inches is equal to [latex]1[/latex] foot. Now, we have [latex]\color{blue}b=2.5[/latex] ft and [latex]\color{red}h=1[/latex] ft.
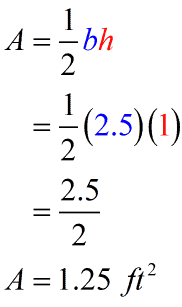
In the same manner, to express the area in square inches, we would keep the height of [latex]12[/latex] inches but convert [latex]2.5[/latex] feet into inches. Since [latex]1[/latex] foot is equal to [latex]12[/latex] inches, that means [latex]2.5[/latex] feet equals [latex]30[/latex] inches, [latex]2.5 \times 12 = 30[/latex]. Finally, we have [latex]\color{blue}b=30[/latex] in. and [latex]\color{red}h=12[/latex] in.
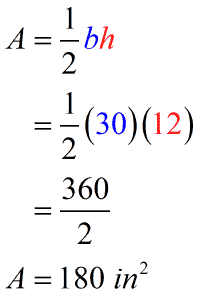
You can give your answer in either [latex]in^2[/latex] or [latex]ft^2[/latex]. It is both correct since
[latex]1.25\,f{t^2} = 180\,\,i{n^2}[/latex].
Example 6: The base of a triangle is [latex]17[/latex] meters. Its area is [latex]204[/latex] square meters. Find the height of the triangle.
This is a very straightforward problem. We substitute the known values into the formula then solve for the leftover variable.
In this case, we know the base [latex]b[/latex] and the area [latex]A[/latex] of the triangle. That means we can solve for the height [latex]h[/latex].
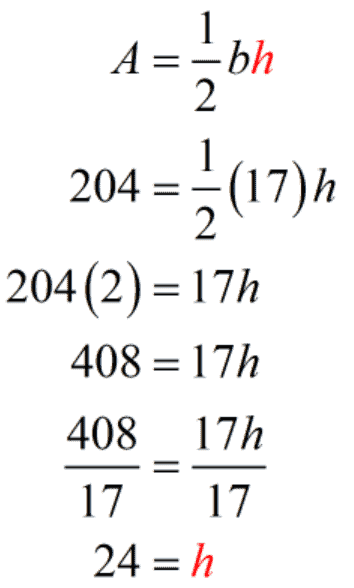
Therefore, the height of the triangle is [latex]24[/latex] meters.
Example 7: The area of a triangle is [latex]162.56[/latex] square centimeters. What is the base of the triangle in inches if the height is [latex]16[/latex] centimeters?
This problem is a combination of examples #5 and #6. After we find the base in centimeters, we will convert it into inches using the conversion factor [latex]1[/latex] in. = [latex]2.54[/latex] cm.
Since the area of the triangle is [latex]162.56[/latex] cm and its height is [latex]16[/latex] cm, we have
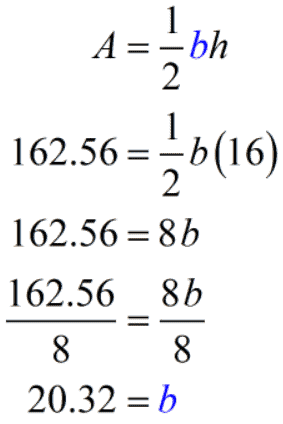
The base is [latex]20.32[/latex] centimeters. However, we still need to convert centimeters to inches to get to our final answer.
Since [latex]1[/latex] in. = [latex]2.54[/latex] cm, we divide [latex]20.32[/latex] by [latex]2.54[/latex] to get to inches.
[latex]{\Large{{{20.32\,} \over {2.54}}}} = 8[/latex]
Therefore, the base is [latex]8[/latex] inches long.
Example 8: The base of a triangle is twice its height. If the area is [latex]289[/latex] square kilometers, find the measure of the base.
It is given that the base is twice its twice, [latex]{\color{blue}b}=2{\color{red}h}[/latex]. So if the height is [latex]h[/latex] then the base is [latex]2h[/latex].
height = [latex]\color{red}h[/latex]
base = [latex]2{\color{red}h}[/latex]
The area is also given as [latex]289[/latex] square kilometers.
Area = [latex]289[/latex]
Plugging these values into the formula and solving for [latex]\color{red}h[/latex].
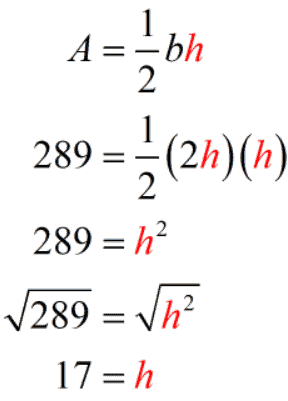
Since the base is [latex]2\color{red}h[/latex], then
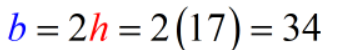
Therefore, the base is [latex]34[/latex] km.
Let’s check if our base and height are correct. For a triangle with a base of [latex]34[/latex] km and a height of [latex]17[/latex] km, the area must be [latex]289[/latex] square km.
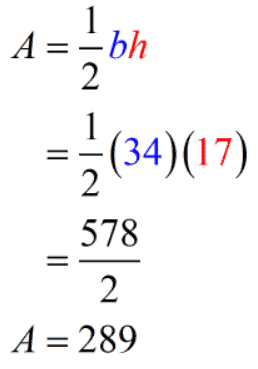
Yes, it checks. That base and height give us an area of [latex]289[/latex] [latex]km^2[/latex].
Example 9: The base of the triangle is [latex]5[/latex] units longer than its height. If the area of the triangle is [latex]117[/latex] square units, what is the measure of the height?
Let [latex]h[/latex] be the height of a triangle. The base is said to be [latex]5[/latex] units longer than the height which can be expressed as [latex]b=h+5[/latex].
Since [latex]b=h+5[/latex] and the area of a triangle is [latex]117[/latex] square units, we can plug this information into the formula to get a quadratic equation solvable using the Factoring Method.
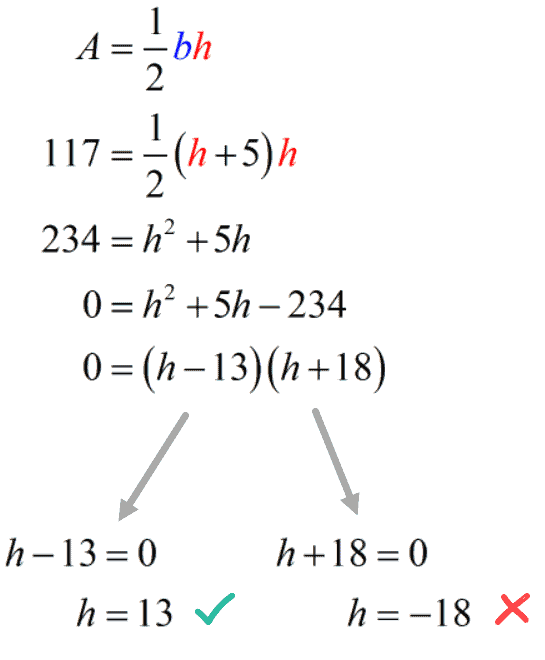
We will ignore the negative solution because there’s no such thing as a negative height.
Therefore, the height is [latex]13[/latex] units.
We can perform a quick check to verify if our answer is correct.
If [latex]h=13[/latex], the base is [latex]13+5=18[/latex]. Calculating the area of the triangle we get
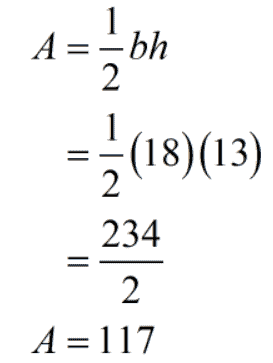
Yes, we get the same area of [latex]117[/latex] square units. That means our values for the base and height are correct!
You may also be interested in these related math lessons or tutorials:
