Altitude of a Triangle

The altitude of a triangle is the perpendicular line segment that is drawn from the vertex of a triangle to the opposite side known as the base, or the line containing the base. Note that the altitude may be perpendicular to the base, or to the extension of the base. By the way, the altitude of a triangle can also be referred to as its “height“.

As you will see in the illustrations below, the altitude of a triangle can be found in three (3) different locations or places. It may lie inside, outside, or be a part of the triangle itself as in the legs of a right triangle.

Case 1: Altitude of Triangle Found Inside

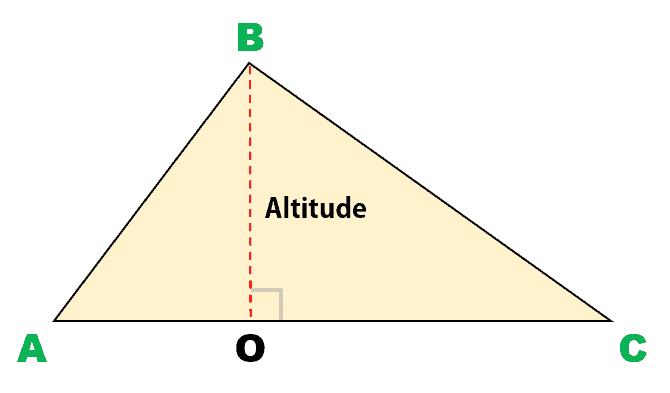
triangle ABC has an altitude that is inside

Line segment [latex]\overline {BO} [/latex] is an altitude formed inside triangle [latex]ABC[/latex]. Notice that [latex]\overline {BO} [/latex] makes a right angle with the opposite side, line segment [latex]\overline {AC} [/latex]

Case 2: Altitude of Triangle Found Outside

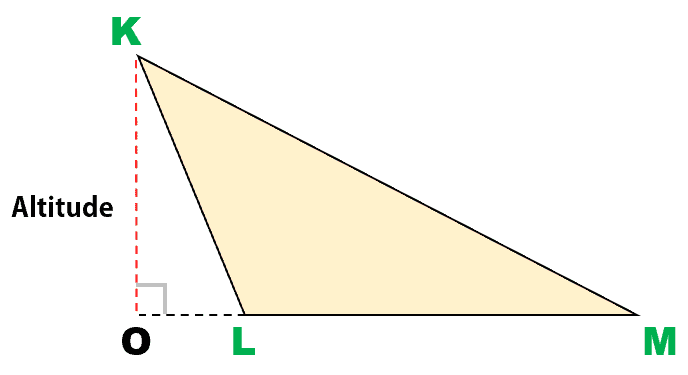
triangle KLM has altitude that is found outside

It is possible for an altitude to lie outside the triangle. In this case, line segment [latex]\overline {KO} [/latex] is an altitude formed outside triangle [latex]KLM[/latex]. Observe that altitude [latex]\overline {KO} [/latex] makes a right angle with the extension of the base [latex] \overline {LM}[/latex].

Case 3: Altitude is Part of the Triangle

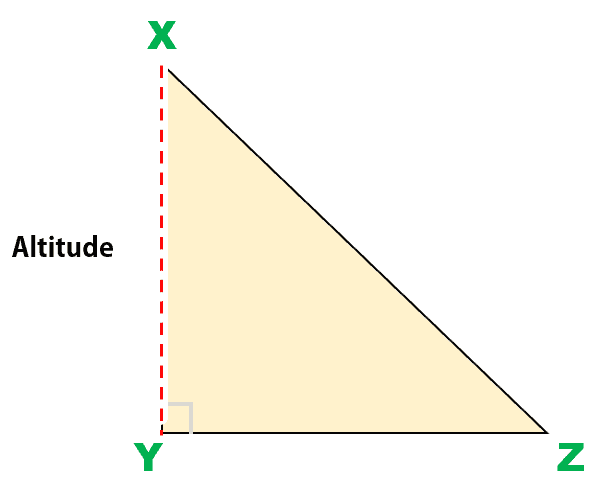
triangle XYZ has an altitude that is part of the triangle itself

In the last two cases, the altitude is either formed inside or outside the triangle. However, it is possible for the altitude to be part of the triangle itself. This happens if the triangle involved is a right triangle. A right triangle is a triangle such that one of its internal angles has a measure of 90 degrees. The reason is that the legs of a right triangle are naturally perpendicular to each other.

Notice that line segment [latex]\overline {XY} [/latex] is a side of triangle [latex]XYZ[/latex] which serves as the altitude as well.

In fact, if we rotate the triangle such that [latex]\overline {ZY} [/latex] is the altitude, it follows that segment [latex]\overline {XY} [/latex] becomes the base.

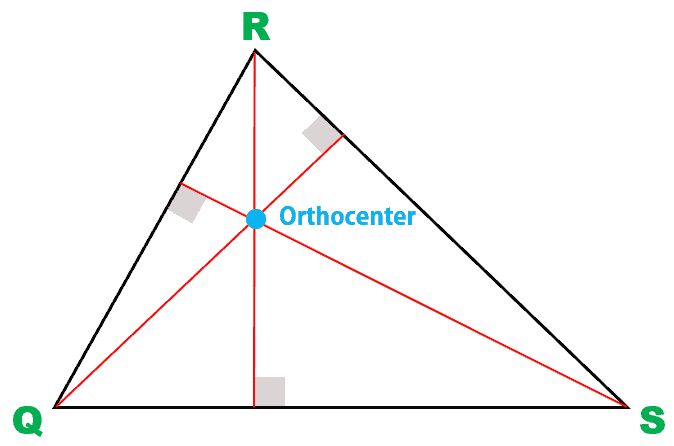
Orthocenter of an Acute Triangle

For an interesting side note, if we draw all the altitudes of an acute triangle, they will intersect at a common point inside the triangle. This point of intersection is known as the orthocenter.

orthocenter is the point of intersection of three altitudes

You may also be interested in these related math lessons or tutorials:

Area of Triangle