Area of Equilateral Triangle Formula
An equilateral triangle is a type of triangle in which all three sides have the same length. In other words, the three sides are congruent. As a result, the three internal angles that are opposite to the sides have also the same measure. That is why an equilateral triangle is also equiangular (all angles are congruent).
The formula to find the area of an equilateral triangle is very simple because we don’t need to know the base or the height of the triangle. The only thing we need is the measure of one side. That’s it!
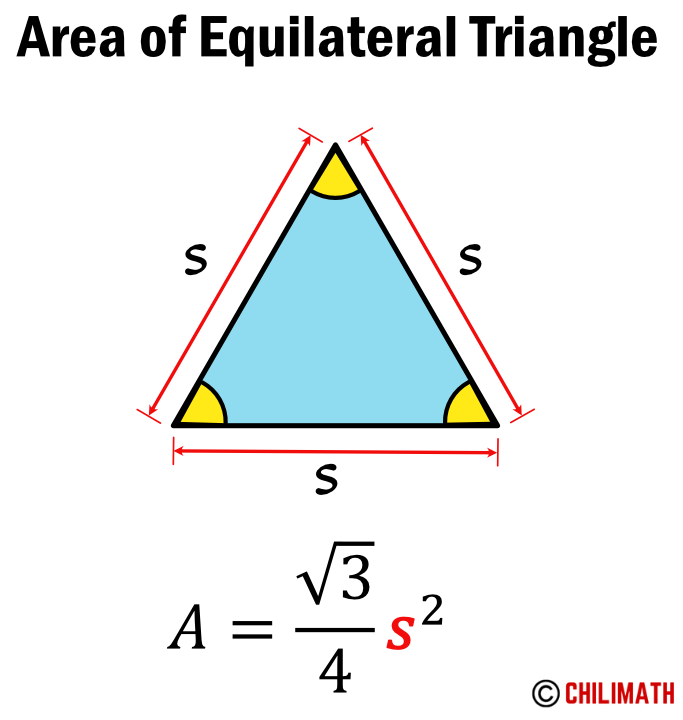
In the area formula above, we multiply the measure of the side length squared [latex]s^2[/latex] by the constant [latex]\large{{\sqrt 3 } \over 4}[/latex]. Notice that the only required input value is the measure of one side of the equilateral triangle, expressed as [latex]\large{s}[/latex] for side.
Before we even start using the formula, it would be nice to know how to derive the formula.
Derivation of Equilateral Triangle Formula
The derivation is really straightforward. It is based on the idea that the area of a triangle is one-half of the base times height. We know the base which is simply one of the sides [latex]s[/latex]. But the height is not given to us. That’s the one we’re going to figure out here.
The first step is to draw an equilateral triangle. Then draw an altitude from the top vertex to the opposite side which is also known as the base. This altitude is both an angle bisector and a perpendicular segment bisector. The altitude of the equilateral triangle also serves as the height of the triangle. Constructing this altitude divides this equilateral triangle into two congruent right triangles.

Let’s focus on one of the right triangles. Notice that this right triangle has a height of [latex]h[/latex], a base of [latex]\Large{{s \over 2}}[/latex], and a hypotenuse of [latex]\large{s}[/latex]. That means we can use the Pythagorean Theorem to calculate the height [latex]h[/latex].
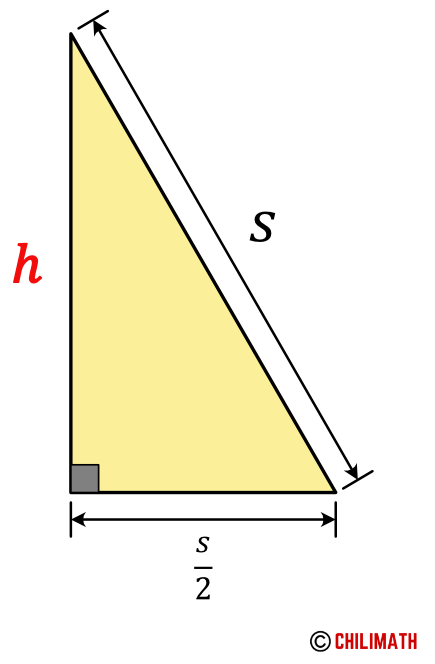
Remember that the Pythagorean Theorem in a nutshell states that if we know the two sides of a right triangle, we can find the third side. For this to work, the triangle must be a right triangle which means one of its angles has a measure of [latex]90[/latex] degrees.

In the Pythagorean Theorem formula, sides [latex]a[/latex] and [latex]b[/latex] are the legs of the right triangle. Notice that the legs form a 90-degree angle which tells us that we are dealing with a right triangle. In addition, the longest side is side [latex]c[/latex] which is the side opposite the 90-degree angle. The longest side of a right triangle has a special name. It’s called the hypotenuse.
So in our original right triangle, the legs have the lengths [latex]h[/latex] and [latex]\Large{s \over 2}[/latex] while hypotenuse is [latex]S[/latex]. We can plug these values into the Pythagorean Theorem formula and solve for the height [latex]h[/latex].
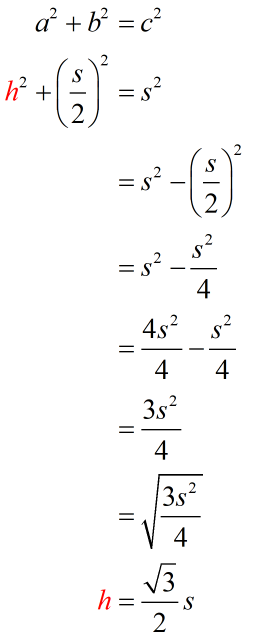
The height of the equilateral triangle is found to be [latex]\large{h = {{\sqrt 3 } \over 2}s}[/latex].
Back to our original equilateral triangle, we can now find the area because we have all the required information.
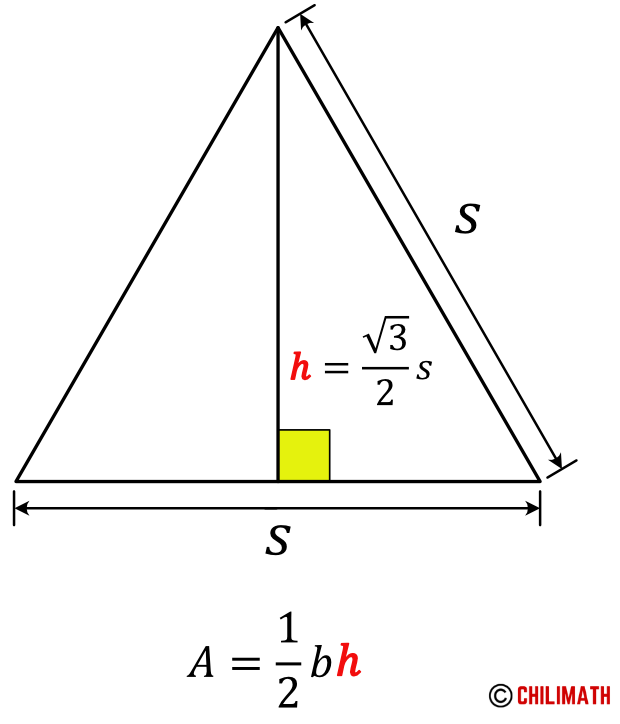
Here, the base is [latex]s[/latex] while the height is [latex]{{{\sqrt 3 } \over 2}s}[/latex]. Let’s substitute these values into the formula to get the formula for area of an equilateral triangle.
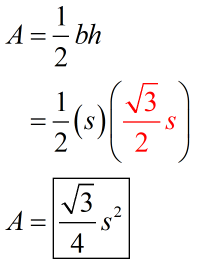
Now that we are able to derive the formula for an equilateral triangle, it’s time to go over some examples!
Area of Equilateral Triangle Formula Examples
Example 1: What is the area of an equilateral triangle with a length of [latex]2[/latex]?
An equilateral triangle is a triangle with three equal sides. We only need to know the measure of one side since they are all the same. It is given that the measure of the side is [latex]2[/latex] which means [latex]s=2[/latex]. Let’s substitute this value into the formula then simplify to get the area of the equilateral triangle.
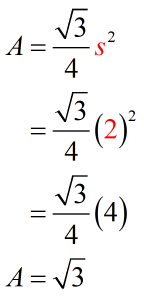
Therefore, the area of the equilateral triangle is [latex]\sqrt 3[/latex] square units which is approximately equal to [latex]1.73[/latex] square units.
Example 2: An equilateral triangle has a side length of [latex]4\sqrt 3[/latex] feet. Find the area of the equilateral triangle.
The length of the equilateral triangle contains a radical symbol. Since we are squaring it in the formula, that will eventually disappear.
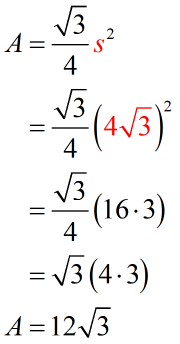
Therefore, the area of the equilateral triangle is [latex]12\sqrt 3[/latex] square feet. This is also approximately equal to [latex]20.78[/latex] square feet.
Example 3: The perimeter of an equilateral triangle is [latex]18[/latex] inches. Calculate the area of the equilateral triangle.
The perimeter of a triangle is the sum of its sides and there are three sides in a triangle. We know that the sides of an equilateral triangle have the same measure. It means we can easily find the side length by dividing the perimeter by [latex]3[/latex].
[latex]s = {P \over 3}[/latex]
[latex] s = {{18} \over 3}[/latex]
[latex] s = 6[/latex]
We found the side of the equilateral triangle to be [latex]6[/latex] inches. Upon knowing the measure of one of its side, we should now be able to find its area using the formula.
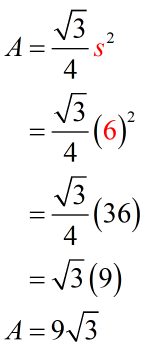
Therefore, the area of the equilateral triangle is [latex]9\sqrt 3[/latex] square inches. This is approximately equal to [latex]15.59[/latex] square inches.
Example 4: The area of an equilateral triangle is [latex]10[/latex] square centimeters. How long is the side of the equilateral triangle?
This formula has only two variables ([latex]A[/latex] and [latex]s[/latex]). If we know the value of one of them, we can solve for the other. Since we are given with the area of the equilateral triangle [latex]A[/latex] that means we can solve for the other variable which is the side [latex]s[/latex].
Let’s plug in the value of the area then solve for the side:
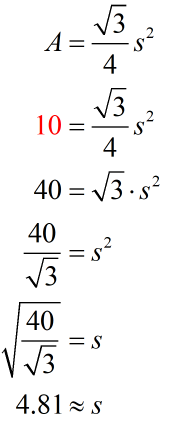
Therefore, the side is about [latex]4.81[/latex] centimeters.
You may also be interested in these related math lessons or tutorials:
