The Pythagorean Theorem
If we have a right triangle, and we construct squares using the edges or sides of the right triangle (gray triangle in the middle), the area of the largest square built on the hypotenuse (the longest side) is equal to the sum of the areas of the squares built on the other two sides. This is the Pythagorean Theorem in a nutshell. By the way, this is also known as the Pythagoras’ Theorem.
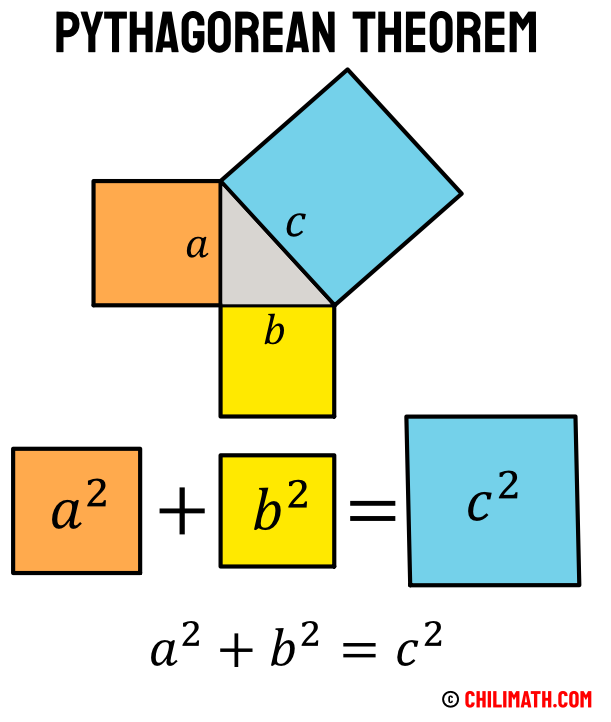
Notice that we square (raised to the second power) the variables [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] to indicate areas. The sum of the smaller squares (orange and yellow) is equal to the largest square (blue).
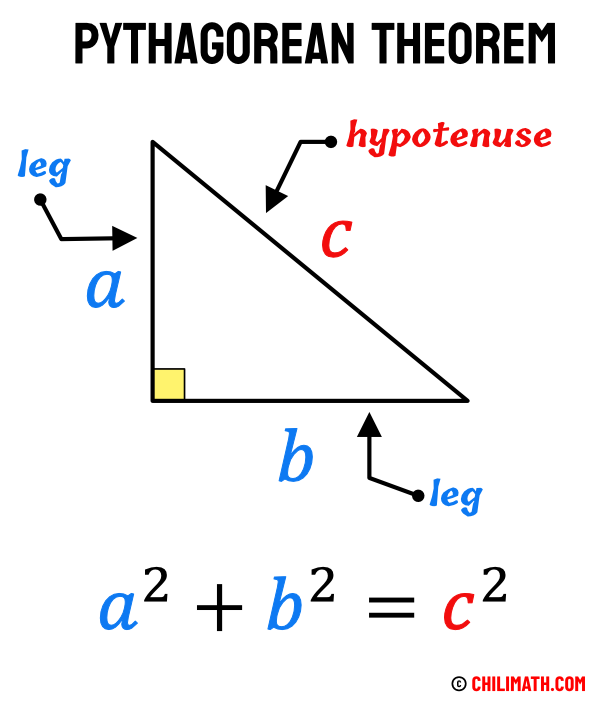
The Pythagorean Theorem relates the three sides in a right triangle. To be specific, relating the two legs and the hypotenuse, the longest side.
The Pythagorean Theorem can be summarized in a short and compact equation as shown below.
Definition of Pythagorean Theorem
For a given right triangle, it states that the square of the hypotenuse, [latex]c[/latex], is equal to the sum of the squares of the legs, [latex]a[/latex] and [latex]b[/latex]. That is, [latex]{a^2} + {b^2} = {c^2}[/latex].
For a more general definition, we have:
In right a triangle, the square of longest side known as the hypotenuse is equal to the sum of the squares of the other two sides.
The Pythagorean Theorem guarantees that if we know the lengths of two sides of a right triangle, we can always determine the length of the third side.
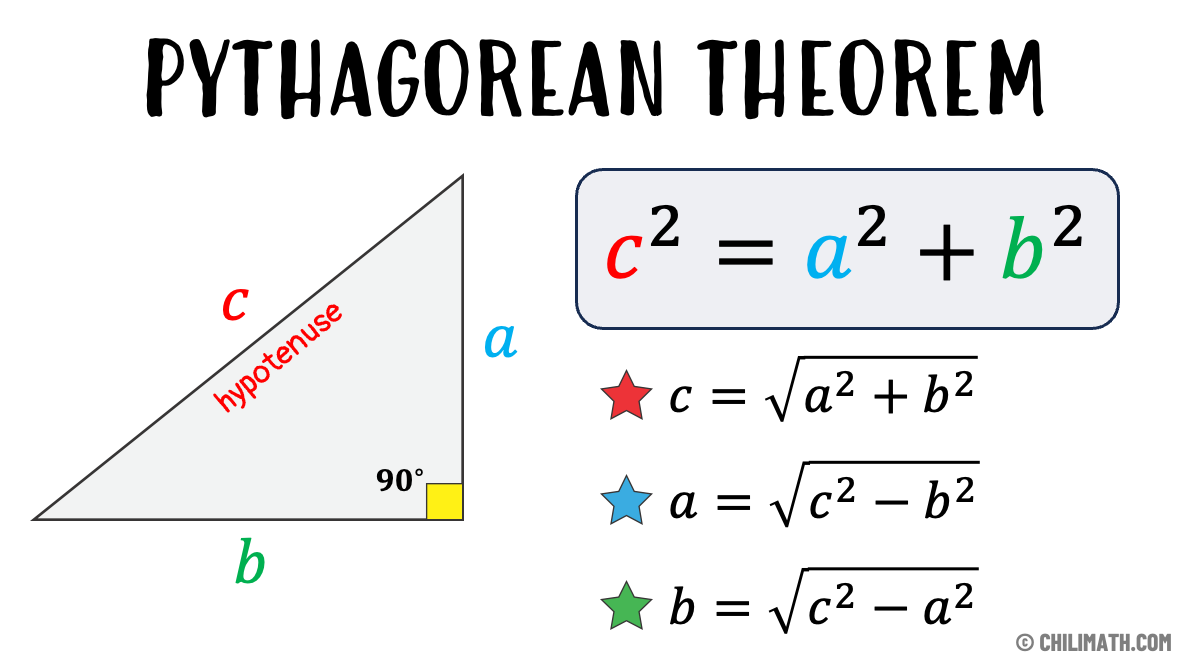
Here are the three variations of the Pythagorean Theorem formulas:

Let’s go over some examples!
Examples of Applying the Pythagorean Theorem
Example 1: Find the length of the hypotenuse.
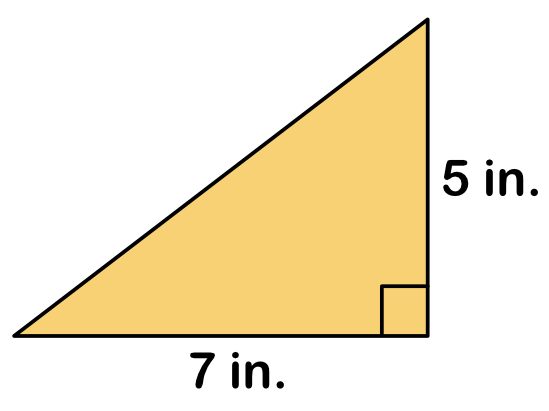
Our goal is to solve for the length of the hypotenuse. We are given the lengths of the two legs. We know two sides out of the three! This is enough information for the formula to work.
For the legs, it doesn’t matter which one we assign for [latex]a[/latex] or [latex]b[/latex]. The result will be the same. So if we let [latex]a=5[/latex], then [latex]b=7[/latex]. Substituting these values into the Pythagorean Formula equation, we get
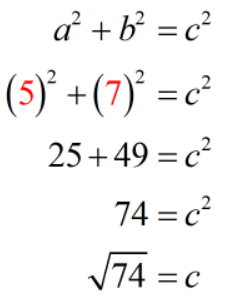
To isolate the variable [latex]c[/latex], we take the square roots of both sides of the equation. That eliminates the square (power of 2) on the right side. And on the left, we simply have a square root of a number which is no big deal.
However, we need to be mindful here when we take the square root of a number. We want to consider only the principal square root or the positive square root since we are dealing with length. It doesn’t make any sense to have a negative length, thus we disregard the negative length!
Therefore, the length of the hypotenuse is [latex]\sqrt {74}[/latex] inches. If we wish to approximate it to the nearest tenth, we have [latex]8.6[/latex] inches.
Example 2: Find the length of the leg.
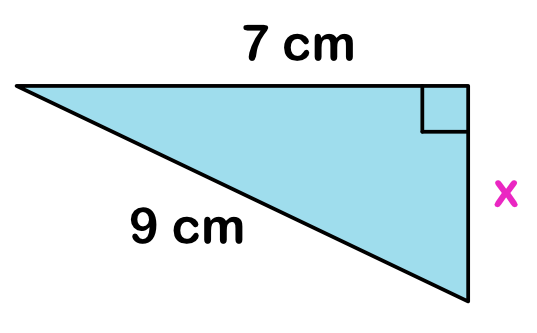
Just by looking at the figure above, we know that we have enough information to solve for the missing side. The reason is the measure of the two sides are given and the other leg is left as unknown. That’s two sides given out of the possible three.
Here, we can let [latex]a[/latex] or [latex]b[/latex] equal [latex]7[/latex]. It really doesn’t matter. So, for this, we let [latex]a=7[/latex]. That means we are solving for the leg [latex]b[/latex]. But for the hypotenuse, there’s no room for error. We have to be certain that we are assigning [latex]c[/latex] for the length, that is, for the longest side. In this case, the longest side has a measure of [latex]9[/latex] cm and that is the value we will assign for [latex]c[/latex], therefore [latex]c=9[/latex].
Let’s calculate the length of leg [latex]b[/latex]. We have [latex]a=7[/latex] and [latex]c=9[/latex].
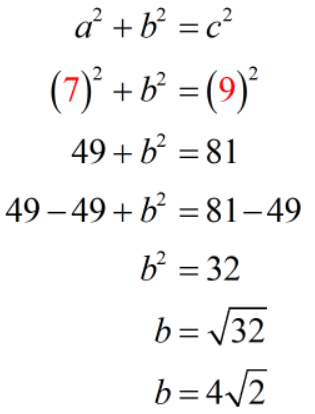
Therefore, the length of the missing leg is [latex]4\sqrt 2[/latex] cm. Rounding it to two decimal places, we have [latex]5.66[/latex] cm.
Example 3: Do the sides [latex]17[/latex], [latex]15[/latex] and [latex]8[/latex] form a right triangle? If so, which sides are the legs and the hypotenuse?
If these are the sides of a right triangle then it must satisfy the Pythagorean Theorem. The sum of the squares of the shorter sides must be equal to the square to the longest side. Obviously, the sides [latex]8[/latex] and [latex]15[/latex] are shorter than [latex]17[/latex] so we will assume that they are the legs and [latex]17[/latex] is the hypotenuse. So we let [latex]a=8[/latex], [latex]b=15[/latex], and [latex]c=17[/latex].
Let’s plug these values into the Pythagorean equation and check if the equation is true.
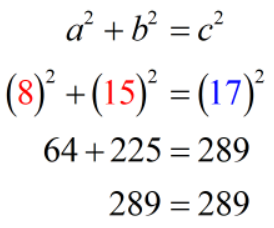
Since we have a true statement, then we have a case of a right triangle! We can now say for sure that the shorter sides [latex]8[/latex] and [latex]15[/latex] are the legs of the right triangle while the longest side [latex]17[/latex] is the hypotenuse.
Example 4: A rectangle has a length of [latex]8[/latex] meters and a width of [latex]6[/latex] meters. What is the length of the diagonal of the rectangle?
The diagonal of a rectangle is just the line segment that connects two non-adjacent vertices. In the figure below, it is obvious that the diagonal is the hypotenuse of the right triangle while the two other sides are the legs which are [latex]8[/latex] and [latex]6[/latex].
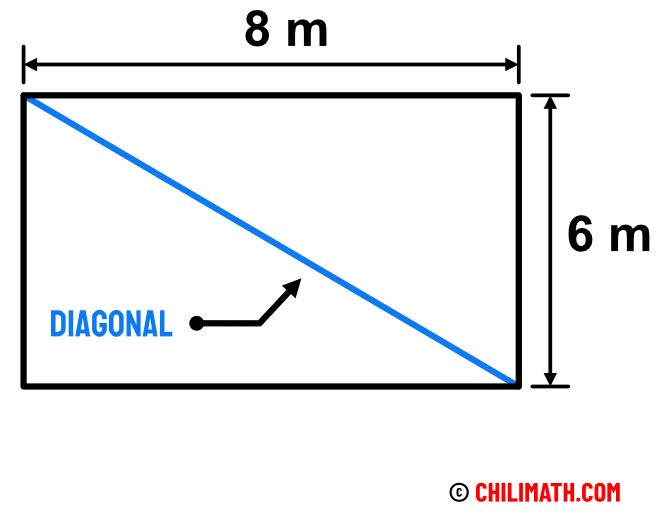
If we let [latex]a=6[/latex] and [latex]b=8[/latex], we can solve for [latex]c[/latex] in the Pythagorean equation which is just the diagonal.
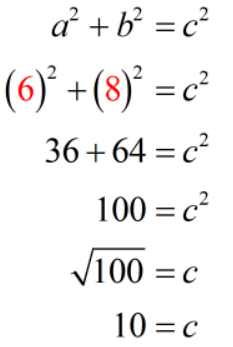
Therefore, the measure of the diagonal is [latex]10[/latex] meters.
Example 5: A ladder is leaning against a wall. The distance from the top of the ladder to the ground is [latex]20[/latex] feet. If the base of the ladder is [latex]4[/latex] feet away from the wall, how long is the ladder?
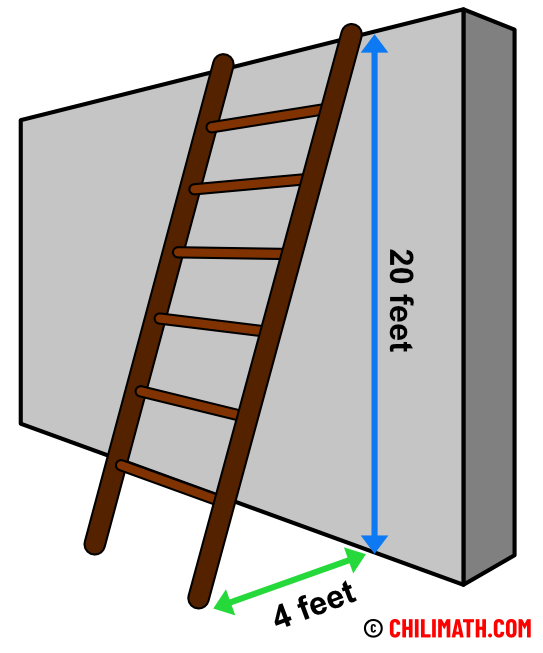
If you study the illustration, the length of the ladder is just the hypotenuse of the right triangle with legs [latex]20[/latex] feet and [latex]4[/latex] feet.
Again, we just need to perform direct substitution into the Pythagorean Theorem formula using the known values then solve for [latex]c[/latex] or the hypotenuse.
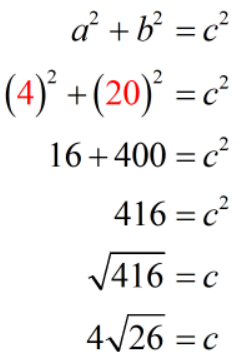
Therefore, the length of the ladder is [latex]4\sqrt {26}[/latex] feet or approximately [latex]20.4[/latex] feet.
Example 6: In a right isosceles triangle, the hypotenuse measures [latex]12[/latex] feet. What is the length of each leg?
Remember that a right isosceles triangle is a triangle that contains a 90-degree angle and two of its sides are congruent.
In the figure below, the hypotenuse is [latex]12[/latex] feet. The two legs are both labeled as [latex]x[/latex] since they are congruent.
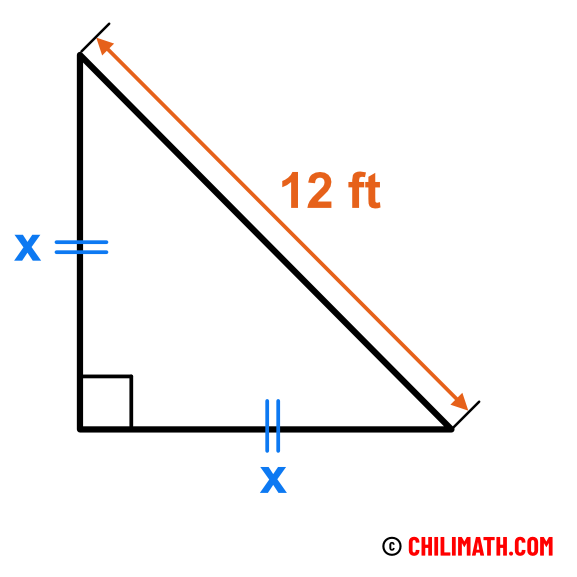
Let’s substitute these values into the formula then solve for the value of [latex]x[/latex]. We know that [latex]x[/latex] is just the leg of the right isosceles triangle which is the unknown that we are trying to solve for.
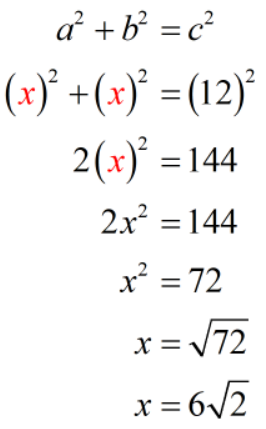
Therefore, the leg of the right isosceles triangle is [latex]6\sqrt 2[/latex] feet. If we want an approximate value, it is [latex]8.49[/latex] feet, rounded to the nearest hundredth.
Example 7: The diagonal of the square below is [latex]2\sqrt 2[/latex]. Find its area.
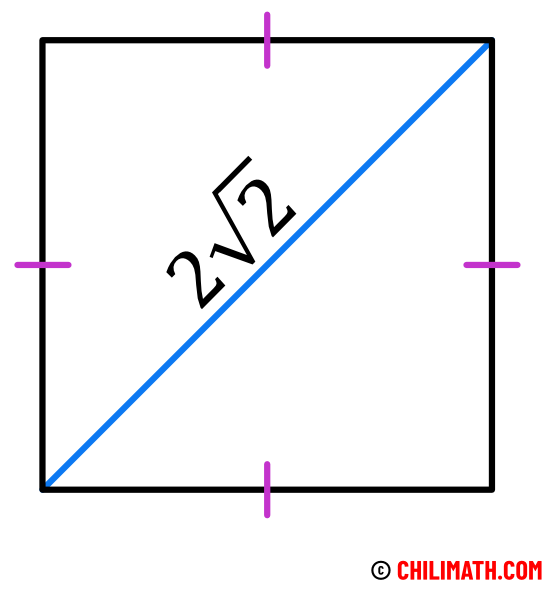
We know the area of the square is given by the formula [latex]A=s^2[/latex] where [latex]s[/latex] is the side of the square. So that means we need to find the side of the square given its diagonal. If we look closely, the diagonal is simply the hypotenuse of a right triangle. More importantly, the legs of the right triangle are also congruent.
Since the legs are congruent, we can let it equal to [latex]x[/latex].
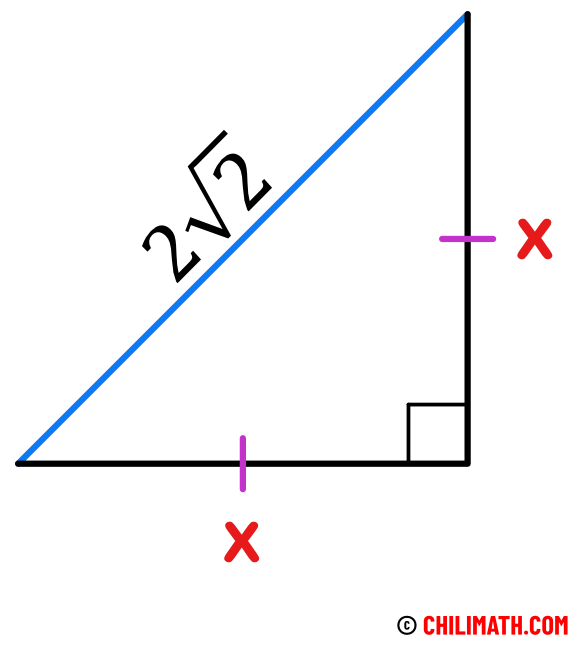
Substitute these values into the Pythagorean Theorem formula then solve for [latex]x[/latex].
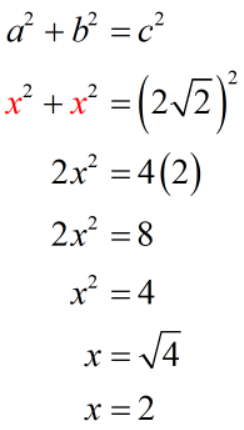
We calculated the length of the leg to be [latex]2[/latex] units. It is also the side of the square. So to find the area of the square, we use the formula
[latex]A = {s^2}[/latex]
That means, the area is
[latex]A = {s^2} = {\left( 2 \right)^2} = 4[/latex]
Therefore, the area of the square is [latex]4[/latex] square units.
You may also be interested in these related math lessons or tutorials:
