Generating Pythagorean Triples using a Formula
You can generate a Pythagorean Triple using a formula. The proof for why this formula always works is beyond the scope of this lesson. For our purposes, let’s call it the ‘Pythagorean Triple Formula’.
Just a note of caution, this formula can generate either a Primitive Pythagorean Triple or an Imprimitive Pythagorean Triple. Remember, the former is a Pythagorean Triple where the Greatest Common Factor is equal to [latex]1[/latex], while the latter has a GCF of greater than [latex]1[/latex].
The Pythagorean Triple Formula

A few observations about the formula:
- The variables [latex]m[/latex] and [latex]n[/latex] are any positive integers. However, positive integer [latex]m[/latex] is greater than positive integer [latex]n[/latex], that is, [latex]m > n[/latex].
- We both use the values of [latex]m[/latex] and [latex]n[/latex] to calculate the lengths of the sides of right triangle ABC which are composed of the two legs [latex]a[/latex] and [latex]b[/latex], and the longest side also known as the hypotenuse, represented by letter [latex]c[/latex].
- The value or length of side [latex]a[/latex] is calculated by finding the difference of the squares of [latex]m[/latex] and [latex]n[/latex]. We can express it in the form of the equation as [latex]a = {m^2} – {n^2}[/latex].
- The length of side [latex]b[/latex] is calculated by doubling the product of [latex]m[/latex] and [latex]n[/latex]. In the equation form, we have [latex]b = 2mn[/latex].
- Finally, the length of side [latex]c[/latex] is computed by getting the sum of the squares of [latex]m[/latex] and [latex]n[/latex]. This can simply be written in the equation as [latex]c = {n^2} + {m^2}[/latex].
Examples of Generating Pythagorean Triples
Example 1: Generate a Pythagorean Triple using the two integers [latex]1[/latex] and [latex]2[/latex].
First, observe that it is possible to generate a Pythagorean Triple with integers [latex]1[/latex] and [latex]2[/latex] because both are positive integers and one is larger than the other. We will let [latex]m[/latex] be equal to [latex]2[/latex] while [latex]n[/latex] be equal to [latex]1[/latex] because [latex]m[/latex] should be greater than [latex]n[/latex] based on the conditions above.
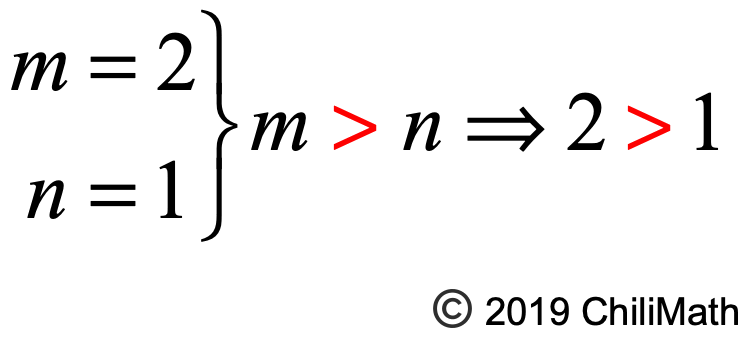
Since we now know what the values of m and n, it’s time to substitute those values into the formulas of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] to obtain the sides of the right triangle.
- Solving for [latex]a[/latex]:
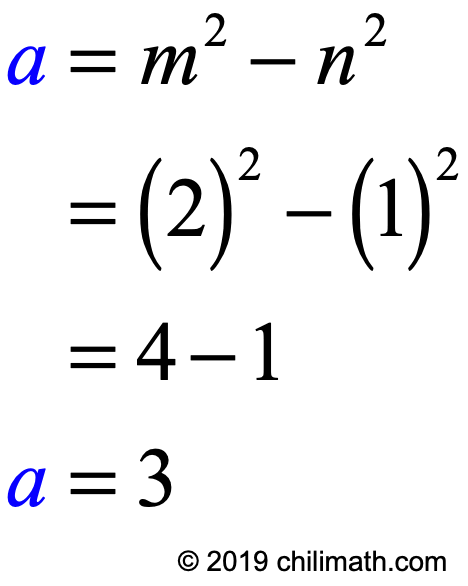
- Solving for [latex]b[/latex]:
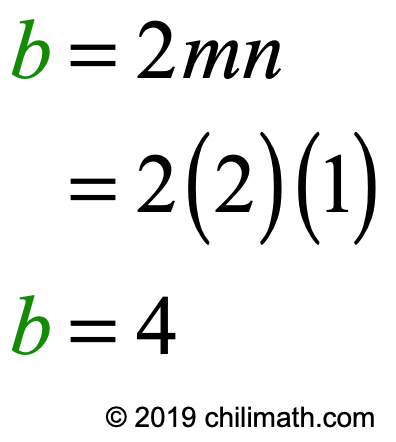
- Solving for [latex]c[/latex]:
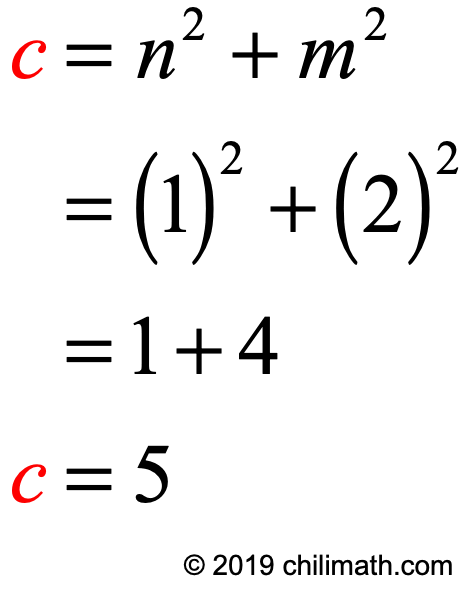
Let’s check if our values for [latex]a=3[/latex], [latex]b=4[/latex], and [latex]c=5[/latex] satisfy the Pythagorean Triple Equation which is [latex]{a^2} + {b^2} = {c^2}[/latex]
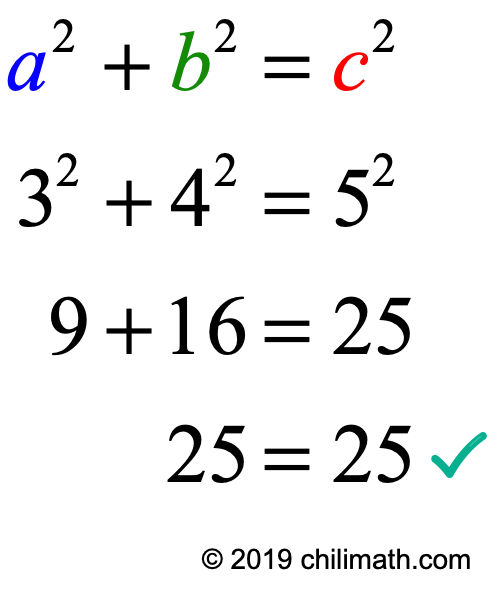
Yes it does! Therefore, (3,4,5) is a Pythagorean Triple.
Example 2: Use the integers 3 and 5 to generate a Pythagorean Triple. Is the generated triple a Primitive or Imprimitive Pythagorean Triple?
The problem above requires us to do two things. First, generate a Pythagorean Triple using the integers [latex]3[/latex] and [latex]5[/latex]. Second, we need to figure out if the generated triple is Primitive or Imprimitive.
Check out my lesson on how to tell if a Pythagorean Triple is Primitive or Imprimitive.
◉ First part:
Since [latex]5[/latex] is greater than [latex]3[/latex], we have [latex]m=5[/latex] and [latex]n=3[/latex]. Solving for [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], we have:
[latex]a = {m^2} – {n^2}[/latex]
[latex]a = {(5)^2} – {(3)^2}[/latex]
[latex]a = 25 – 9[/latex]
[latex]a = 16[/latex]
[latex]b = 2mn[/latex]
[latex]b = 2\left( 5 \right)\left( 3 \right)[/latex]
[latex]b = 30[/latex]
[latex]c = {n^2} + {m^2}[/latex]
[latex]c = {\left( 3 \right)^2} + {\left( 5 \right)^2}[/latex]
[latex]c = 9 + 25[/latex]
[latex]c = 34[/latex]
Upon checking with the required formula, we verify that indeed (16, 30, 34) is a Pythagorean Triple.
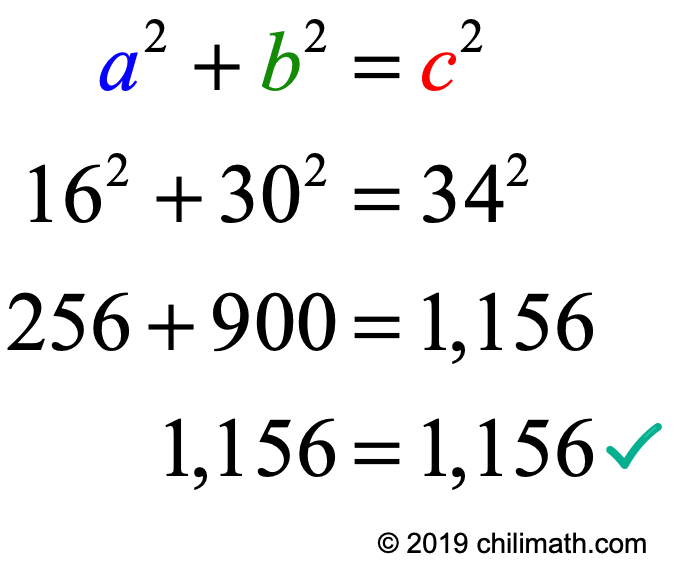
◉ Second part:
Now, we want to know if our generated Pythagorean Triple is primitive or imprimitive.
Remember that a Pythagorean Triple is primitive if all three integers have a common factor of ONLY 1.
Otherwise, it is not primitive (imprimitive) since it has a common factor OTHER THAN 1.
By quick inspection, the Pythagorean Triple, (16, 30, 34), contains all even numbers. That means it has a factor other than [latex]1[/latex] because all integers are divisible by [latex]2[/latex]. In other words, the triplet in question has more than [latex]1[/latex] common factors. Therefore, (16, 30, 34) is an Imprimitive Pythagorean Triple.
Example 3: What is the Pythagorean Triple generated by the integers 3 and 10? Is the generated triplet primitive or non-primitive?
Since [latex]10 > 3[/latex] then [latex]m = 10[/latex] and [latex]n = 3[/latex] because integer [latex]m[/latex] must be larger than integer [latex]n[/latex] .
At this point, you should already be familiar with the formula. Let’s solve for [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] then.
- Computing for [latex]a[/latex] :
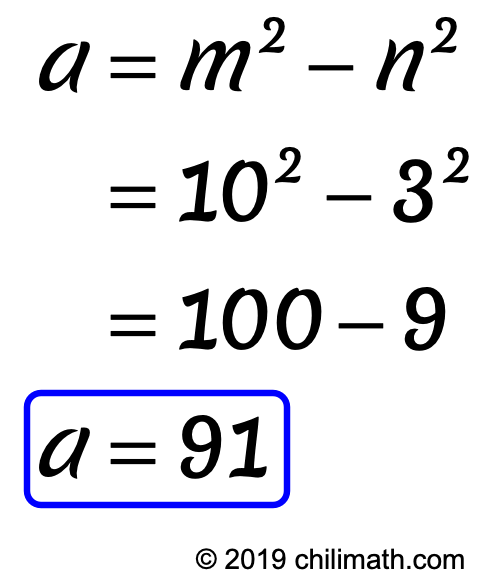
- Solving for [latex]b[/latex] :

- Calculating for [latex]c[/latex] :
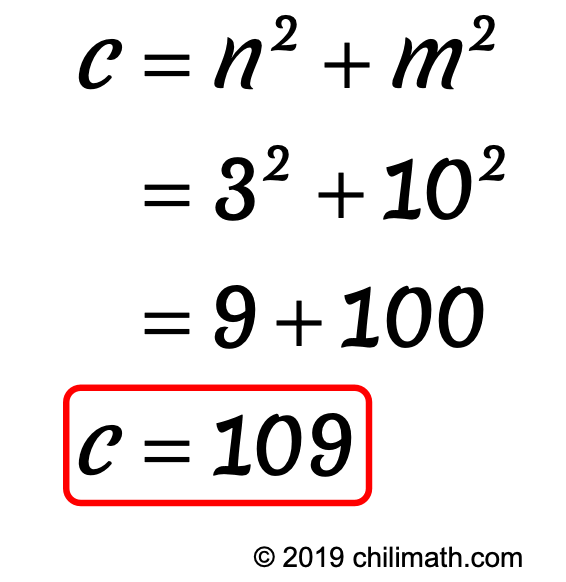
Verifying the values of [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] with the Pythagorean Triple equation which is
[latex]\left( {a,b,c} \right)[/latex]
[latex]{a^2} + {b^2} = {c^2}[/latex]
we have,
[latex]\left( {91,60,109} \right)[/latex]
[latex]{91^2} + {60^2} = {109^2}[/latex]
[latex]{91^2} + {60^2} = {109^2}[/latex]
[latex]{8,281} + {3,600} = {11,881}[/latex]
[latex]{11,881} = {11,881}[/latex]
Yes! It checks. It means that [latex]\left( {91,60,109} \right)[/latex] is indeed a Pythagorean Triple.
By quick inspection, we can tell that the integers 90, 60, and 109 have a Greatest Common Divisor of 1 which makes it a Primitive Pythagorean Triple.
You may also be interested in these related math lessons or tutorials:
Pythagorean Theorem Practice Problems with Answers
