Prove: Suppose [latex]n[/latex] is an integer. If [latex]n^2[/latex] is even, then [latex]n[/latex] is even.

Let [latex]\color{red}n[/latex] be an integer. We want to show that whenever [latex]\large{\color{red}n^2}[/latex] is even, then [latex]\large{\color{red}n}[/latex] must be even.

Just a heads-up, the result of this theorem is significant because it will help you prove a more important fact [in the future] that the square root of 2 is irrational. But, let’s disregard it for now.

The proof of the theorem above is actually very simple. But before we begin writing the proof, we will review some background knowledge that is relevant to proving the theorem in question.

◉ First, we need to describe how even and odd numbers look algebraically. I have separate lessons dedicated to even and odd numbers.

Remember that an even number can be expressed as [latex]2k[/latex] where [latex]k[/latex] is an integer. For example, the number [latex]6[/latex] is even since we can rewrite it as the product of [latex]2[/latex] and some integer [latex]k[/latex]. Thus, [latex]6 = 2\left( k \right) \to 6 = 2\left( 3 \right)[/latex].

On the other hand, an odd number can be expressed as [latex]2k+1[/latex] or [latex]2k-1[/latex] where [latex]k[/latex] is just an integer. For instance, we can rewrite the odd number [latex]13[/latex] as [latex]13 = 2\left( 6 \right) + 1[/latex] or [latex]13 = 2\left( 7 \right) – 1[/latex].

◉ Secondly, we need to know how to write the contrapositive of a statement. The reason is that if it is hard or impossible to prove a statement by direct proof, then the workaround is to prove its contrapositive. We can do this because they are logically the same.

So, for the conditional statement [latex]{\color{blue}p} \to {\color{red}q}[/latex] (read as “p implies q”) its contrapositive is written as ~[latex]\color{red}q[/latex] [latex]\to[/latex] ~[latex]\color{blue}p[/latex] (read as “not q implies not p”).

---

Observe how the contrapositive is constructed from the original statement.

• The hypothesis [latex]{\color{blue}p}[/latex] and the conclusion [latex]{\color{red}q}[/latex] are swapped.

• Then, the new hypothesis [latex]{\color{red}q}[/latex] and the new conclusion [latex]{\color{blue}p}[/latex] are both negated. The tilde symbol ~ is often used to denote negation.

---

Examples of the Contrapositive of a Conditional Statement

• Example 1

• Example 2

• Example 3

---

As you already know, a statement and its contrapositive are logically equivalent. That means if the conditional statement is true, its contrapositive is also true. On the other hand, if the conditional statement is false, its contrapositive must also be false. Thus, the conditional statement and its contrapositive are either both true or both false. This is what it means to be logically equivalent.

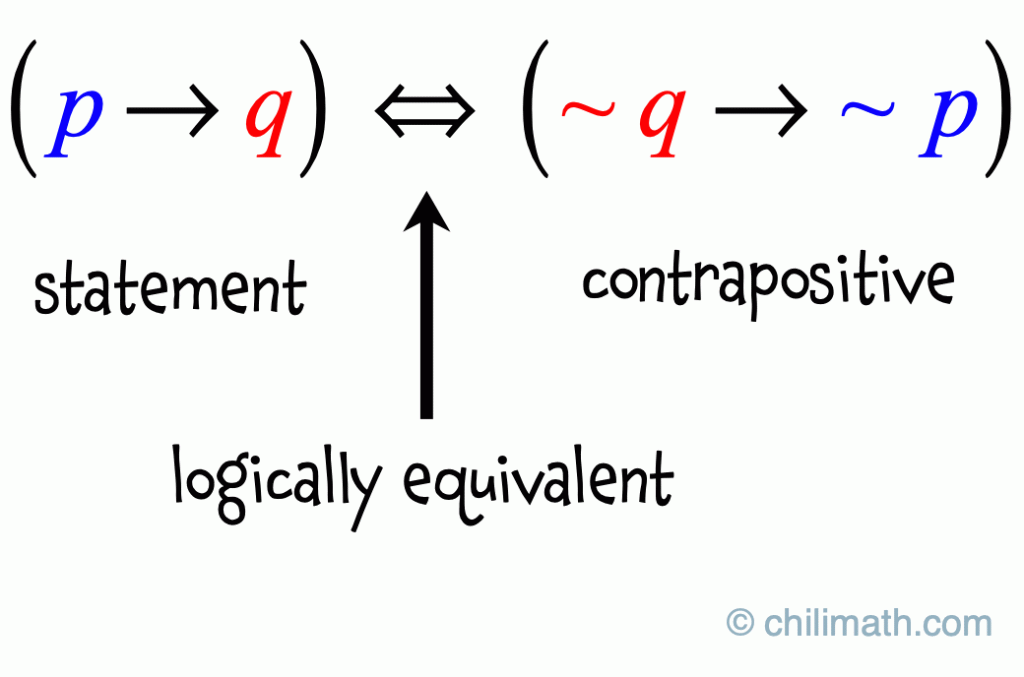
So here’s the main takeaway.

Proving the contrapositive of a statement is logically the same as proving the statement itself.

---

BRAINSTORM BEFORE WRITING THE PROOF

Equipped with the background knowledge that we discussed above regarding even and odd numbers, and the contrapositive of a statement, then we are ready to tackle the proof.

Here is the theorem again that we want to prove.

• Suppose [latex]\color{red}n[/latex] is an integer.

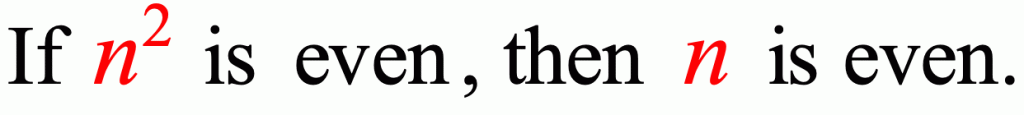
It is impossible to prove the statement as it stands, therefore we need a different strategy to approach this. In fact, we should always consider proof by contrapositive if the direct proof of the original statement seems to be difficult. Remember, proving the contrapositive of a statement is logically the same as proving the original statement.

Since the original statement is

• If [latex]n^2[/latex] is even, then [latex]n[/latex] is even.

The contrapositive is

• If [latex]n[/latex] is not even, then [latex]n^2[/latex] is not even.

But there is a better way of saying “not even”. If you think about it, the opposite of an even number is odd number.

Rewrite the contrapositive as

If [latex]n[/latex] is odd, then [latex]n^2[/latex] is odd.

Since [latex]n[/latex] is odd (hypothesis), we can let [latex]n = 2k + 1[/latex] for some integer [latex]k[/latex]. Then we are going to square it as the conclusion suggests, and show that it is odd.

Is the square of an odd number or [latex]2k + 1[/latex] also an odd number? Let’s do the math.

[latex]{\left( {2k + 1} \right)^2} = 4{k^2} + 4k + 1[/latex]

Factor out [latex]\color{red}2[/latex] from the first two terms of the trinomial which are [latex]4{k^2}[/latex] and [latex]4{k}[/latex].

[latex]4{k^2} + 4k + 1 = {\color{red}2}\left( {2{k^2} + 2k} \right) + 1[/latex]

Focus your attention to the algebraic expression inside the parenthesis which is [latex]{2{k^2} + 2k}[/latex]. Since [latex]k[/latex] is some integer, then both [latex]{2{k^2}}[/latex] and [latex]{2k}[/latex] are integers as well. Adding them together, [latex]{2{k^2} + 2k}[/latex], we get a sum that is also an integer.

The reason why we made those claims is because of the fact that the set of integers is close under the operations of addition and multiplication. In other words, we made those justifications using the Closure Properties of Addition and Multiplication over the set of integers. The symbol for the set of integers is [latex]\mathbb{Z}[/latex].

Since we established that [latex]{2{k^2} + 2k}[/latex] is also integer, we can let [latex]{2{k^2} + 2k}[/latex] equal to [latex]r[/latex] where [latex]r[/latex] is just another integer. Thus, [latex]r = 2{k^2} + 2k[/latex]

Now, we can safely substitute the expression [latex]{2{k^2} + 2k}[/latex] inside the parenthesis by [latex]r[/latex].

[latex]4{k^2} + 4k + 1 = {\color{red}2}\left( {2{k^2} + 2k} \right) + 1[/latex]

[latex]4{k^2} + 4k + 1 = {\color{red}2}\left( {r} \right) + 1[/latex]

The right hand side (RHS) of the equation which is [latex]2r + 1[/latex] is an odd number by definition. We have reached our goal to show that the square of an odd number, [latex]{\left( {2k + 1} \right)^2}[/latex], is also odd.

---

WRITE THE PROOF

THEOREM: Let [latex]n[/latex] be an integer. If [latex]n^2[/latex] is even, then [latex]n[/latex] is even.

PROOF: We will prove this theorem by proving its contrapositive. The contrapositive of the theorem: Suppose [latex]n[/latex] is an integer. If [latex]n[/latex] is odd, then [latex]n^2[/latex] is odd. Since [latex]n[/latex] is odd then we can express [latex]n[/latex] as [latex]n = 2{\color{red}k} + 1[/latex] for some integer [latex]\color{red}k[/latex]. Next, we square [latex]n[/latex], thus [latex]{n^2} = {\left( {2k + 1} \right)^2}[/latex]. Expand the square of the binomial [latex]{\left( {2k + 1} \right)^2}[/latex] to get [latex]{\left( {2k + 1} \right)^2} = 4{k^2} + 4k + 1[/latex]. Factor out [latex]2[/latex] from the first two terms of the trinomial, we have [latex]4{k^2} + 4k + 1 = 2\left( {2{k^2} + 2k} \right) + 1[/latex]. Since [latex]k[/latex] is an integer, then [latex]{2{k^2} + 2k}[/latex] must also be an integer by the Closure Property of Addition and Multiplication over the set of integers ([latex]\mathbb{Z}[/latex]). Let [latex]r = 2{k^2} + 2k[/latex], thus [latex]2\left( {2{k^2} + 2k} \right) + 1[/latex] becomes [latex]2r + 1[/latex] which is clearly an odd number. Since we proved the contrapositive to be true, then the original statement must also be true. Therefore, we have proved that if [latex]n^2[/latex] is even, then [latex]n[/latex] is even.◼︎

---

You might also be interested in:

Prove: Suppose n is an integer. If [latex]n^2[/latex] is odd, then [latex]n[/latex] is odd.