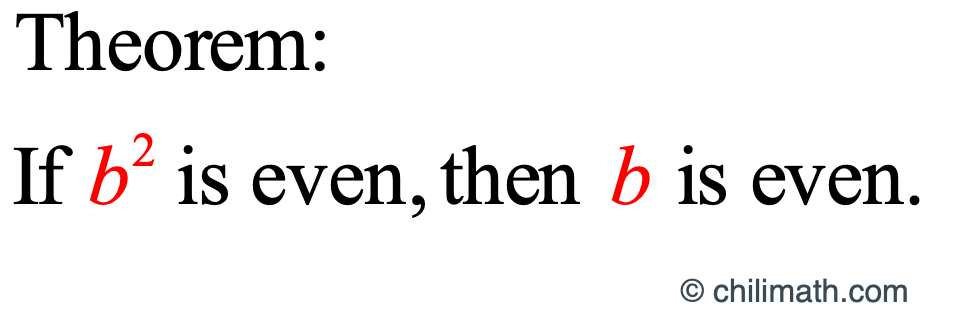Prove: The Square Root of [latex]2[/latex], [latex]\sqrt 2 [/latex], is Irrational.
Proving that [latex]\color{red}{\sqrt2}[/latex] is irrational is a popular example used in many textbooks to highlight the concept of proof by contradiction (also known as indirect proof). This proof technique is simple yet elegant and powerful.
Basic steps involved in the proof by contradiction:
- Assume the negation of the original statement is true.
- Prove the assumption. You may utilize any proof techniques such as direct proof and proof by contraposition.
- When you reach a contradiction, state that the assumption is false, hence the original statement must be true.
BRAINSTORM BEFORE WRITING THE PROOF
To prove that the square root of [latex]2[/latex] is irrational is to first assume that its negation is true. Therefore, we assume that the opposite is true, that is, the square root of [latex]2[/latex] is rational.

You may wonder what our next step be. Well, the assumption should give us a hint on where to start. Since we assume that [latex]\sqrt 2[/latex] is rational, we must describe or express [latex]\sqrt 2[/latex] as a rational number.
If [latex]\sqrt 2[/latex] is a rational number, then we can express it as a ratio of two integers.
So, [latex]\sqrt 2 = {\Large{{a \over b}}}[/latex] where [latex]a[/latex] and [latex]b[/latex] are integers but [latex]b \ne 0[/latex].
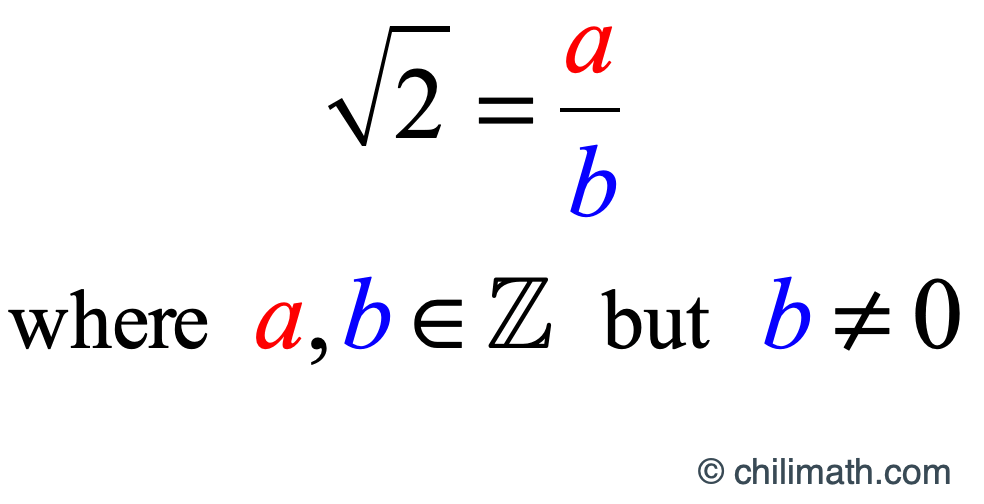
Now, here is the trick that makes the proof by contradiction work. We will further assume that [latex]a[/latex] and [latex]b[/latex] are relatively prime or co-prime. Two integers are said to be relatively prime if they share no common positive divisors other than [latex]1[/latex].
More so, [latex]\Large{a \over b}[/latex] is an irreducible fraction because the integers [latex]a[/latex] and [latex]b[/latex] have a Greatest Common Factor (GCF) of [latex]1[/latex].
Now, let’s press on. Since we established that [latex]\sqrt 2 = {\Large{{a \over b}}}[/latex], we square both sides of the equation to eliminate the square root symbol.
[latex]\sqrt 2 = {\Large{{a \over b}}}[/latex]
[latex]{\left( {\sqrt 2 } \right)^2} = {\Large{{\left( {{a \over b}} \right)^2}}}[/latex]
[latex]2 = {\Large{{{a^2}} \over {{b^2}}}}[/latex]
Multiply both sides of the equation by [latex]b^2[/latex] to get rid of the denominator on the right side of the equation.
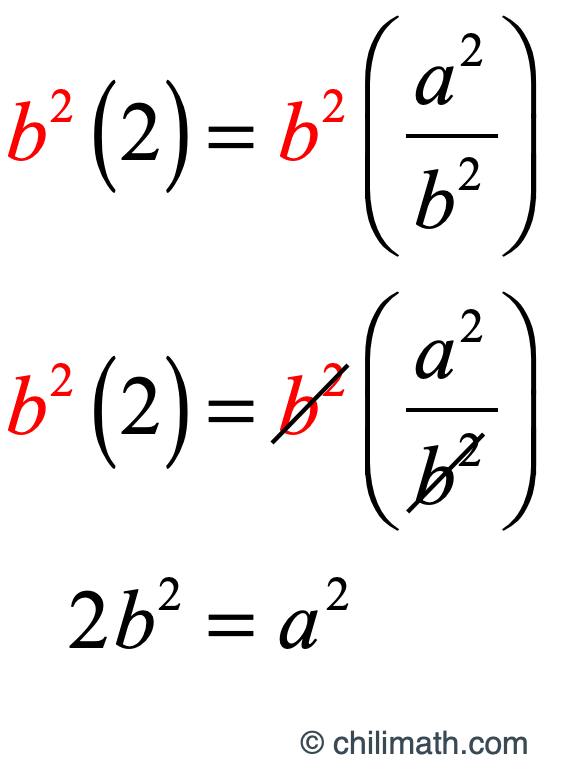
What does it tell us about [latex]a^2[/latex] in [latex]2{b^2} = {a^2}[/latex] or [latex]{a^2} = 2{b^2}[/latex] ? Since [latex]a^2[/latex] is equal to [latex]2[/latex] times some integer [latex]b^2[/latex], then [latex]a^2[/latex] is by definition an even number.
From the result of a previous theorem, we know that if [latex]a^2[/latex] is an even number, then [latex]a[/latex] is also an even number.
Suppose [latex]\Large\color{red}{a}[/latex] is an integer.
Since we deduce that [latex]\color{red}a[/latex] is even, we can express it as [latex]{\color{red}a}=2k[/latex] for some integer [latex]k[/latex].
Now, let’s back up a little where we have the setup [latex]2{b^2} = {a^2}[/latex]. We can substitute [latex]2k[/latex] for [latex]\color{red}a[/latex] in the equation then simplify.
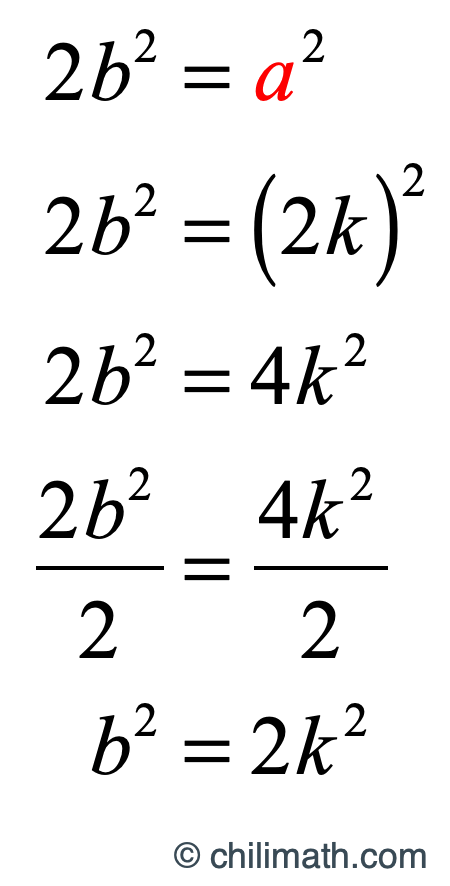
After doing some algebra on the equation, the outcome is very interesting because the result tells us that [latex]b^2[/latex] is even. Using again the consequence of the theorem below, we can claim that since [latex]b^2[/latex] is even, then [latex]b[/latex] must also be even. If you need a refresher on this topic, click the image below to take you to the lesson.
Let [latex]\Large\color{red}{b}[/latex] an integer.
Our findings show that both [latex]\color{red}a[/latex] and [latex]\color{blue}b[/latex] are even numbers. It implies that they have at least one common positive divisor other than [latex]1[/latex] which is [latex]2[/latex].
This directly contradicts our assumption that the ratio [latex]\Large{{a \over b}}[/latex] is an irreducible fraction because they share no positive divisors except [latex]1[/latex].
The consequence of this contradiction is to reject the assumption and therefore declare that the original statement must be true. That is, [latex]\sqrt 2[/latex] is indeed irrational.
We will put all these thoughts together when we write our proof.
WRITE THE PROOF
THEOREM: [latex]\sqrt 2[/latex] is irrational.
PROOF: For the sake of contradiction, suppose [latex]\sqrt 2[/latex] is NOT irrational. That means we assume that [latex]\sqrt 2[/latex] is rational. Since [latex]\sqrt 2[/latex] is rational, express it as a ratio of two integers [latex]\Large{a \over b}[/latex] where [latex]a[/latex] and [latex]b[/latex] belong to the set of integers but [latex]b \ne 0[/latex]. Thus, [latex]\sqrt 2 = \Large{{a \over b}}[/latex]. Square both sides of the equation [latex]{\left( {\sqrt 2 } \right)^2} = \Large{{\left( {{a \over b}} \right)^2}}[/latex] to get [latex]2 = \Large{{{{a^2}} \over {{b^2}}}}[/latex].
Multiplying both sides by [latex]b^2[/latex], we have [latex]2{b^2} = {a^2}[/latex]. Since [latex]a^2[/latex] is equal to the product of [latex]2[/latex] and some integer [latex]b^2[/latex], it implies [latex]a^2[/latex] is even. From the previous theorem we have proved, we know that if [latex]a^2[/latex] is even, then [latex]a[/latex] is even. Since [latex]a[/latex] is an even number, we can express it as [latex]a = 2k[/latex] for some integer [latex]k[/latex].
Substituting [latex]2k[/latex] for [latex]a[/latex] in [latex]2{b^2} = {a^2}[/latex], we obtain [latex]2{b^2} = {\left( {2k} \right)^2}[/latex] which can be further simplified as [latex]2{b^2} = 4{k^2}[/latex]. Now, divide both sides by [latex]2[/latex], we get [latex]{b^2} = 2{k^2}[/latex]. Applying the same theorem like before, if [latex]b^2[/latex] is even, then [latex]b[/latex] is even.
We have discovered that both [latex]a[/latex] and [latex]b[/latex] are even numbers. Since [latex]a[/latex] and [latex]b[/latex] are even, it means that they have a common positive divisor other than [latex]1[/latex]. An example is [latex]2[/latex]. We have contradicted our assumption that [latex]\Large{{{a \over b}}}[/latex] is irreducible which means they share no common positive divisors except [latex]1[/latex]. Because our assumption is found to be false, the original statement that [latex]\sqrt 2 [/latex] is irrational must be true. Therefore, [latex]\sqrt 2 [/latex] is an irrational number. ◼︎
You may also be interested in these related math lessons or tutorials:
Let n be an integer. If n^2 is even, then n is even.