The Even Numbers
An even number is an integer that can be divided exactly by [latex]2[/latex]. When an even number is divided by [latex]2[/latex], the remainder is zero.
By performing mental math, it’s obvious that the numbers below, including the negative numbers, are even because they are all divisible by 2.

In addition, I want to point out that many students think zero is neither even nor odd.
Believe me, zero is considered an even number for the same simple reason that it is also an integer that is divisible by [latex]2[/latex] thus no remainder when divided by [latex]2[/latex]. That is, [latex]0 \div 2 = 0[/latex].
Observation: We can generalize from the examples above that even numbers always end [latex]0[/latex], [latex]2[/latex], [latex]4[/latex], [latex]6[/latex], or [latex]8[/latex].
However, there is a better way to define an even number because it’s more mathematically precise. Here it is!
General Form of an Even Number
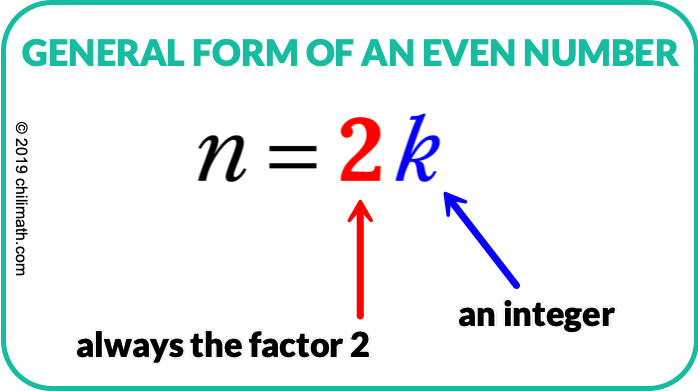
DEFINITION: The number [latex]\large{n}[/latex] is an even number if we can express it as [latex]\large{2k}[/latex] where [latex]\large{k}[/latex] is just another integer.
Examples of Even Numbers Expressed in General Form
Let’s put the general form of an even number to the test. Whatever math concept we’re presented with, it is crucial that we verify it.
Below are a few examples to showcase the concept of an even number as [latex]n = 2\,k[/latex] where [latex]k[/latex] is an integer.
[latex]\color{red}\LARGE {n = 2k}[/latex]
- [latex]0 \to 0 = 2\left( 0 \right)[/latex]
- [latex]14 \to 14 = 2\left( 7 \right)[/latex]
- [latex] – 32 \to – 32 = 2\left( { – 16} \right)[/latex]
- [latex]50 \to 50 = 2\left( {25} \right)[/latex]
- [latex] – 78 \to – 78 = 2\left( { – 39} \right)[/latex]
The constant appearance of [latex]2[/latex] as one of the factors of an even number suggests that any even numbers are indeed a multiple of [latex]2[/latex].
You may also be interested in these related math lessons or tutorials:
