Prove: Let [latex]n[/latex] be an integer. If [latex]{n^2}[/latex] is odd, then [latex]n[/latex] is odd.
We assume that [latex]\large{n}[/latex] is an integer. Our goal is to show that [latex]\large{n^2}[/latex] is odd is a sufficient condition to justify that [latex]\large{n}[/latex] is odd.
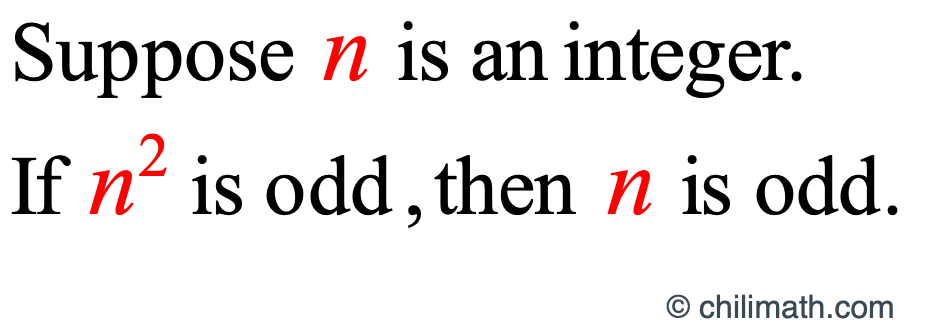
Down the road, you will appreciate the result of this theorem as it will be very useful in proving the fact that the square root of 2 is irrational.
There is no need to reinvent the wheel. I have already written a proof that is very similar to this. I invite you to check it out and come back here. I promise that once you have gone over my other lesson, proving this theorem is a piece of cake. Below is the link:
Prove: Suppose [latex]n[/latex] is an integer. If [latex]n^2[/latex] is even, then n is even.
However, I will quickly cover the prerequisites in this lesson so you may not need to visit the link above.
REVIEW OF IMPORTANT CONCEPTS
◉ First, learn how to write the contrapositive of an If-Then Statement (also known as a Conditional Statement).
The contrapositive of
If [latex]\color{blue}p[/latex], then [latex]\color{red}q[/latex]
is
If ~[latex]\color{red}q[/latex], then ~[latex]\color{blue}p[/latex].
- The tilde symbol ~ is used to denote the negation or opposite of a statement.
- Remember that the conditional statement is logically equivalent to its contrapositive. Therefore, [latex]{\color{blue}p} \to {\color{red}q}[/latex] [latex] \equiv [/latex] ~[latex]\color{red}q[/latex] [latex]\to[/latex] ~[latex]\color{blue}p[/latex]. That means if the conditional stamement is true, its contrapositive is also true. In addition, when the conditional statement is false, so is its contrapositive.
- Example: The contrapositive of the conditional statement “If a number is rational, then it can be expressed as a ratio of two integers” is “If a number cannot be expressed as a ratio of two integers, then the number is irrational”.
- Another example: The conditional statement “If [latex]\color{blue}{n^2}+1[/latex] is odd, then [latex]\color{red}n[/latex] is even” is logically equivalent to its contrapositive which is “If [latex]\color{red}n[/latex] is odd, then [latex]\color{blue}{n^2}+1[/latex] is even”.
◉ Secondly, recognize that an even number can be expressed as the product of [latex]2[/latex] and an integer, that is, [latex]2k[/latex] for some integer [latex]k[/latex].
- Examples of even numbers written in the form [latex]2k[/latex].
[latex]6=2(3)[/latex]
[latex]18=2(9)[/latex]
[latex]30=2(15)[/latex]
BRAINSTORM BEFORE WRITING THE PROOF
The current form of the statement will be impossible to prove using the direct proof method. It’s natural for us to seek an alternative strategy to prove it. Proof by contraposition should be your second option if direct proof fails. Though I can argue that proof by contradiction is also a viable method.
Let’s write the contrapositive of the theorem that we want to prove.
The contrapositive of the following statement
If [latex]n^2[/latex] is odd, then [latex]n[/latex] is odd.
is
If [latex]n[/latex] is even, then [latex]n^2[/latex] is even.
Don’t forget that if the contrapositive is proven true, the original statement must be also true.
Assume that [latex]n[/latex] is even that means we can express it as [latex]n = 2k[/latex]. Now, substitute the expression for [latex]n[/latex] which is [latex]2k[/latex] into [latex]n^2[/latex], the conclusion.
That gives us
[latex]{n^2} = {\left( {2k} \right)^2}[/latex]
[latex]{n^2} = 4{k^2}[/latex]
Factor out [latex]2[/latex] from the right hand side of the equation
[latex]{n^2} = {\color{red}2}\left( {2{k^2}} \right)[/latex]
Focus your attention on the monomial inside the parenthesis. Since [latex]k[/latex] is an integer, then [latex]2k^2[/latex] must also be an integer by the Closure Property of Multiplication over the set of integers denoted by the symbol [latex]\mathbb{Z}[/latex]. Let [latex]r=2k^2[/latex] so we can replace [latex]2k^2[/latex] by [latex]r[/latex].
[latex]{n^2} = 2r[/latex]
Where [latex]2r[/latex] is clearly the algebraic form of an even number.
WRITE THE PROOF
THEOREM: Assume [latex]n[/latex] to be an integer. If [latex]n^2[/latex] is odd, then [latex]n[/latex] is odd.
PROOF: By contraposition: Suppose [latex]n[/latex] is an integer. If [latex]n[/latex] is even, then [latex]n^2[/latex] is even. Since [latex]n[/latex] is an even number, we let [latex]n=2k[/latex]. Substitute [latex]2k[/latex] for [latex]n[/latex] into [latex]n^2[/latex]. Now we have [latex]{n^2} = {\left( {2k} \right)^2} = 4{k^2}[/latex]. Factor out [latex]2[/latex] to get [latex]4{k^2} = 2\left( {2{k^2}} \right)[/latex]. Since [latex]k[/latex] is an integer so is [latex]2k^2[/latex]. Substitute [latex]2k^2[/latex] by some integer [latex]r[/latex]. Therefore, [latex]4{k^2} = 2\left( {2{k^2}} \right) = 2r[/latex] which is clearly an even number. We have proved the contrapositive to be true. That makes the original conditional statement true as well. Hence, we have proved that if [latex]n^2[/latex] is odd, then [latex]n[/latex] is odd. ◼︎
You may also be interested in these related math lessons or tutorials:
