What is an Odd Number?
A number is considered odd if it cannot be equally divided by the number [latex]2[/latex]. It follows that since it is not divisible by [latex]2[/latex], any odd numbers are also not multiples of [latex]2[/latex].
What do you think would happen if you add [latex]+1[/latex] to any even numbers? Try to perform some calculations in your head and observe what you get.
Below are some examples to illustrate the case when an even number is increased by [latex]1[/latex].
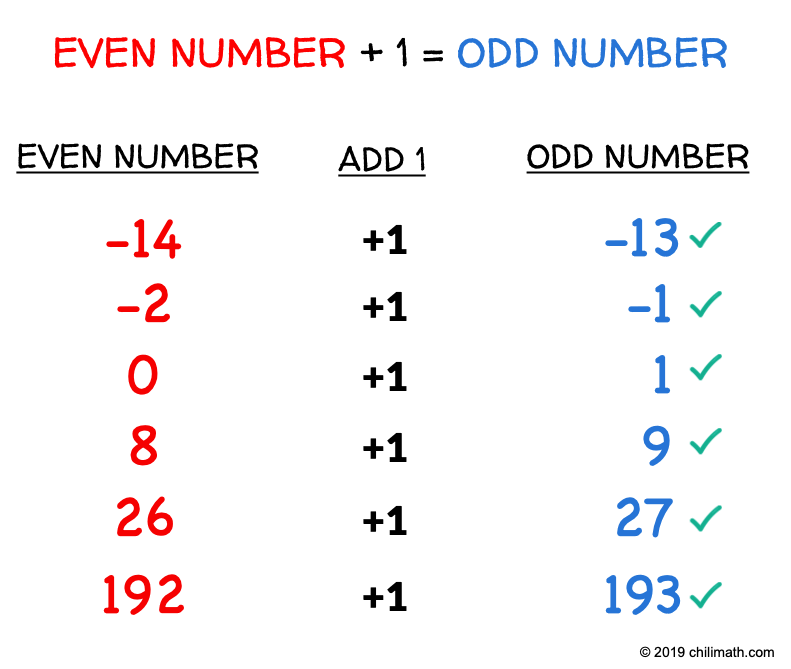
We can now describe the general form of an odd number. Notice, it’s very similar to the general form of an even number which is [latex]n = 2k[/latex]. We simply add 1 to it. That’s why we arrive at [latex]n = 2k + 1[/latex]. In fact, the remainder of an odd number when divided by [latex]2[/latex] is always [latex]+1[/latex].
General Form of an Odd Number
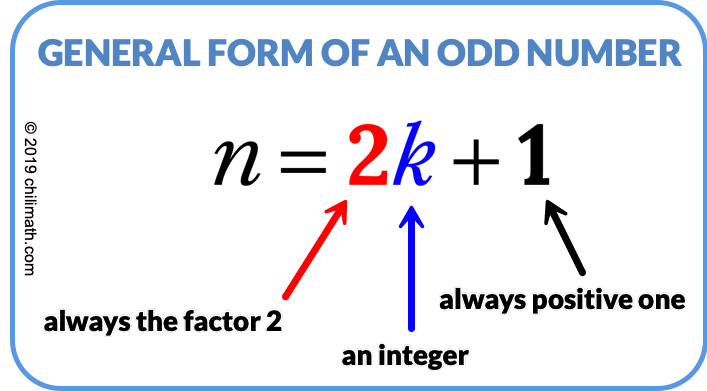
DEFINITION: The number [latex]\large{n}[/latex] is an odd number if it can be expressed as [latex]\large{2k+1}[/latex] where [latex]\large{k}[/latex] is just another integer.
Examples of Odd Numbers Written in General Form
Let’s put it to the test if indeed an odd number [latex]\textbf{n}[/latex] can be expressed in the form [latex]\textbf{n = 2k + 1}[/latex] where [latex]\textbf{k}[/latex] is also an integer.
[latex]\color{red}\LARGE n = 2k + 1[/latex]
- [latex] – 109 \to – 109 = 2\left( { – 55} \right) + 1[/latex]
- [latex] – 13 \to – 13 = 2\left( { – 7} \right) + 1[/latex]
- [latex] – 5 \to – 5 = 2\left( { – 3} \right) + 1[/latex]
- [latex] – 1 \to – 1 = 2\left( { – 1} \right) + 1[/latex]
- [latex]7 \to 7 = 2\left( 3 \right) + 1[/latex]
- [latex]23 \to 23 = 2\left( {11} \right) + 1[/latex]
- [latex]49 \to 49 = 2\left( {24} \right) + 1[/latex]
- [latex]101 \to 101 = 2\left( {50} \right) + 1[/latex]
- [latex]377 \to 377 = 2\left( {188} \right) + 1[/latex]
- [latex]1,013 \to 1,013 = 2\left( {506} \right) + 1[/latex]
You may also be interested in these related math lessons or tutorials:
