Learning how to solve radical equations requires a lot of practice and familiarity of the different types of problems. In this lesson, the goal is to show you detailed worked solutions of some problems with varying levels of difficulty.

There are seven (7) problems in this lesson.

Example 1: Solve the radical equation .

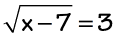
The radical is by itself on one side so it is fine to square both sides of the equations to get rid of the radical symbol. Then proceed with the usual steps in solving linear equations.

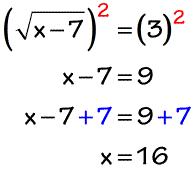
You must ALWAYS check your answers to verify if they are "truly" the solutions. Some answers from your calculations may be extraneous. Substitute x = 16 back into the original radical equation to see whether it yields a true statement.

Yes it checks, so x = 16 is a solution.

---

Example 2: Solve the radical equation .

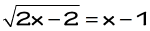
The setup looks good because the radical is again isolated on one side. So I can square both sides to eliminate that square root symbol. Be careful dealing with the right side when you square the binomial (x − 1). You must apply the FOIL method correctly.

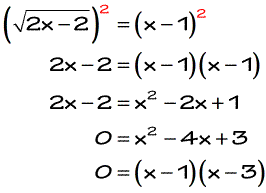
We move all the terms to the right side of the equation , and then proceed on factoring out the trinomial. Applying the Zero-Product Property, we obtain the values of x = 1 and x = 3.

Caution: Always check your calculated values from the original radical equation to make sure that they are true answers and not extraneous or "false" answers.

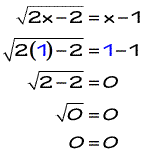
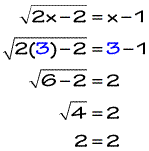
Looks good for both of our solved values of x after checking, so our solutions are x = 1 and x = 3.

---

Example 3: Solve the radical equation .

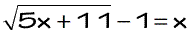
We need to recognize the radical symbol is not isolated just yet on the left side. It means we have to get rid of that −1 before squaring both sides of the equation. A simple step of adding both sides by 1 should take care of that problem. After doing so, the "new" equation is similar to the ones we have gone over so far.

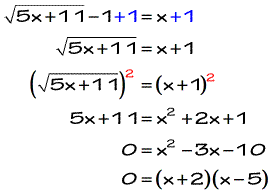
Our possible answers are x = −2 and x = 5. Notice I use the word "possible" because it is not final until we perform our verification process of checking our values against the original radical equation.

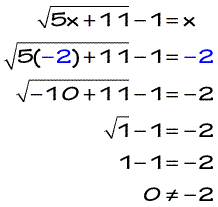
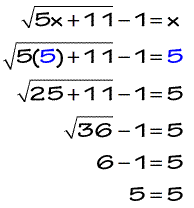
Since we arrive at a false statement when x = −2, therefore that value of x is considered to be extraneous so we disregard it! Leaving us with one true answer, x = 5.

---

Example 4: Solve the radical equation .

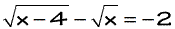
The left side looks a little messy because there are two radical symbols. But it is not that bad! Always remember the key steps suggested above. Since both of the square roots are in one side that means it's definitely ready for the entire radical equation to be squared.

So for our first step, let's square both sides and see what happens.

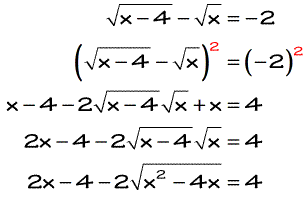
It is perfectly normal in this type of problem to see another radical symbol after the first application of squaring. The good news coming out from this is that there's only one left. From this point, try to isolate again the single radical on the left side, that should force us to relocate the rest to the opposite side.

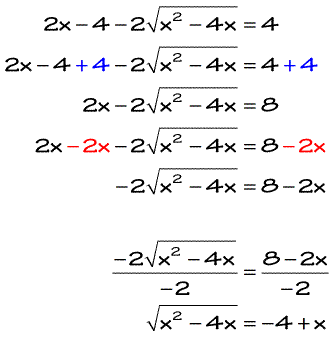
As you can see, that simplified radical equation is definitely familiar. Proceed with the usual way of solving it and make sure that you always verify the solved values of x against the original radical equation.

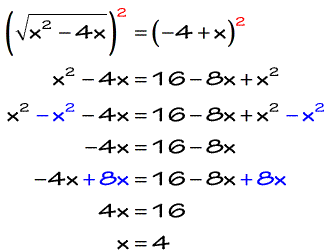
I will leave to you to check that indeed x = 4 is a solution.

---

Example 5: Solve the radical equation .

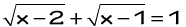
This problem is very similar to example 4. The only difference is that this time around both of the radicals have binomial expressions. The approach is also to square both sides since the radicals are on one side, and simplify. But we need to perform second application of squaring to fully get rid of the square root symbol.

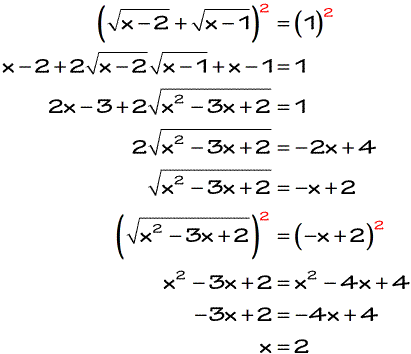
The solution is x = 2, and you may verify it by substituting the value back into the original radical equation and see that it yields a true statement.

---

Example 6: Solve the radical equation .

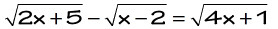
It looks like our first step is to square both sides and observe what comes out afterwards. Don't forget to combine like terms every time you square the sides. If it happens that another radical symbol is generated after the first application of squaring process, then it makes sense to do it one more time. Remember, our goal is to get rid of the radical symbols to free up the variable we are trying to solve or isolate.

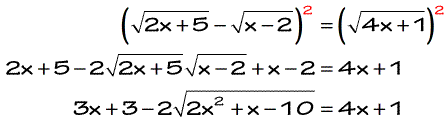
Well, it looks like we will need to square both sides again because of the new generated radical symbol. But we must isolate the radical first on one side of the equation before doing so. I will keep the square root on the left, and that forces me to move everything to the right.

 

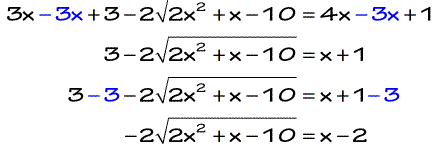
Looking good so far! Now it's time to square both sides again to finally eliminate the radical.

Be careful though in squaring the left side of the equation. You must also square that −2 to the left of the radical.

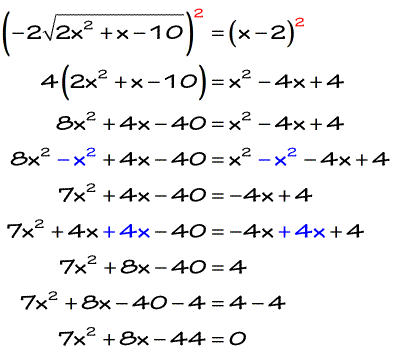
What we have now is a quadratic equation in the standard form. The best way to solve for x is to use the Quadratic Formula where a = 7, b = 8, and c = −44.

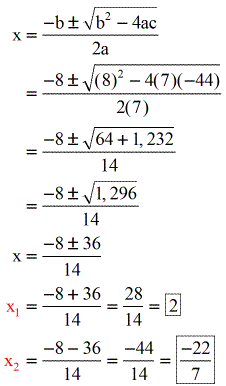
So the possible solutions are x = 2, and x = .

I will leave it to you to check those two values of "x" back into the original radical equation. I hope you agree that x = 2 is the only solution while the other value is actually extraneous, so disregard it!

---

Example 7: Solve the radical equation .

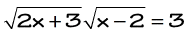
There are two ways to approach this problem. I could immediately square both sides to get rid of the radicals or multiply the two radicals first then square. Both procedures should arrive at the same answers when properly done. For this I will use the second approach.

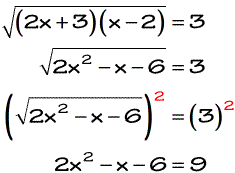
Next, move everything to the left side and solve the resulting Quadratic equation.  You can use the Quadratic formula to solve it, but since it is easily factorable I will just factor it out.

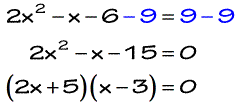
The possible solutions then are and .

I will leave it to you to check the answers. The only answer should be x = 3 which makes the other one as extraneous solution.