How to Rationalize the Denominator
To rationalize the denominator means to eliminate any radical expressions in the denominator such as square roots and cube roots. The key idea is to multiply the original fraction by an appropriate value, such that after simplification, the denominator no longer contains radicals.
Note: In this lesson, we will only focus on square roots for the sake of simplicity.
When the denominator is a monomial, the basic strategy is to apply the fact that
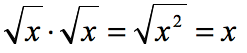
Conjugate of a Binomial
On the other hand, if the denominator is a binomial, the notion of conjugate comes in handy. The conjugate of a binomial is equal to the binomial itself, however, the middle sign is changed or switched.
Here are some examples of binomials with their corresponding conjugates. But more importantly, observe that the product of a given binomial and its conjugate is an expression without the radical symbol.
![a table showing four kinds of binomial with a radical term and their corresponding conjugates. it also shows the product of a binomial with a radical term and its conjugate. for example, [a+sqrt(b)] multiplied by [a-sqrt(b)] =a^2 - b.](https://www.chilimath.com/wp-content/uploads/2018/12/table-binomial-conjugates.png)
Let’s go over some examples!
Examples of How to Rationalize the Denominator
Example 1: Rationalize the denominator [latex]\large{{5 \over {\sqrt 2 }}}[/latex]. Simplify further, if needed.
The denominator contains a radical expression, the square root of [latex]2[/latex]. Eliminate the radical at the bottom by multiplying by itself which is [latex]\sqrt 2[/latex] since [latex]\sqrt 2 \cdot \sqrt 2 = \sqrt 4 = 2[/latex] .
However, by doing so we change the “meaning” or value of the original fraction. To balance it out, do the same thing on top by multiplying with the same value.
What we are doing here is multiplying the original fraction by [latex]\large{{{\sqrt 2 } \over {\sqrt 2 }}}[/latex] which is just equivalent to [latex]1[/latex].
Remember that any number, when multiplied to [latex]1[/latex], gives back the original number, thus, we change the form but not the original meaning of the number itself!
So then the simple solution to this problem is shown below.
![5/sqrt(2) multiplied by sqrt(2)/sqrt(2) = [5*sqrt(2)]/sqrt(4)= [5 sqrt(2)]/2](https://www.chilimath.com/wp-content/uploads/2018/12/ratex1.png)
The final answer contains a denominator without a radical symbol, and so we can claim that we have successfully rationalized it.
Example 2: Rationalize the denominator [latex]\large{{6 \over {\sqrt 3 }}}[/latex]. Then simplify if necessary.
Observe that the denominator has a square root of [latex]3[/latex]. We have the need to rationalize it by getting rid of the radical symbol.
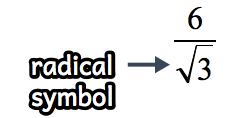
That means we should multiply the original fraction by [latex]\large{{{\sqrt 3 } \over {\sqrt 3 }}}[/latex].
![6/sqrt(3) * sqrt(3)/sqrt(3) = [6*sqrt(3)]/3 = 2*sqrt(3)](https://www.chilimath.com/wp-content/uploads/2018/12/example-1-step1.png)
Yes, the radical symbol at the bottom is gone but we can still do something. Simplify further by canceling out common factors.
Example 3: Rationalize [latex]\large{\sqrt {{{27} \over {12}}}}[/latex].
What we have here is a square root of an entire fraction. The first step is to apply the Quotient Rule of Square Roots. This allows us to generate a fraction with a distinct numerator and a denominator with radical symbols.
QUOTIENT RULE OF SQUARE ROOTS
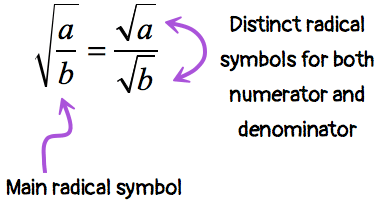
By applying the rule above, we get a problem that is more familiar to us.
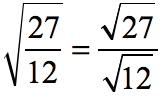
The “new” form of the given problem has a denominator of root [latex]12[/latex] ,so we will multiply it by [latex]\large{{{\sqrt {12} } \over {\sqrt {12} }}}[/latex].
![sqrt(27)/sqrt(12) = [{sqrt(27))(sqrt(12}]/12](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex3a.png)
As you can see, I did not multiply through the radicals on the numerator because the number will grow larger, thus more difficult to simplify. This way we should be able to simplify the numerator quite easily since the radicands are smaller when they are kept as is.
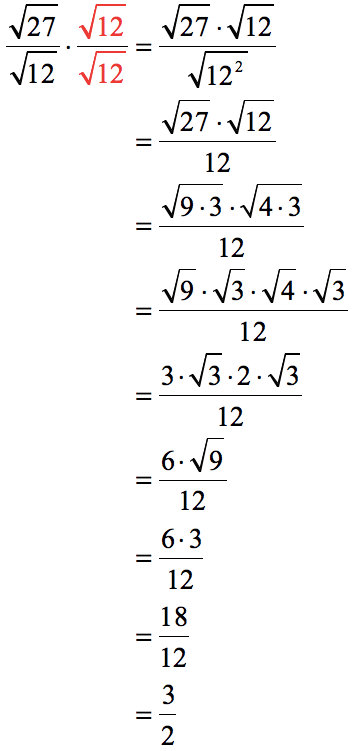
Example 4: Simplify by rationalizing the denominator of [latex]\large{{{7\sqrt {10} } \over {\sqrt 2 }}}[/latex].
Multiply both the numerator and denominator by [latex]\sqrt 2 [/latex] . By doing so, the radical in the denominator should go away.
![(7)[sqrt(10)]/sqrt(2) = (7)[sqrt(20)]/2](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex4a.png)
We can’t stop here just yet because the radical expression in the numerator contains a perfect square factor. Let’s keep going with our simplification.
![(7)[sqrt(10)]/sqrt(2) = (7)[sqrt(5)]](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex4c.png)
Cancel out common factors to get the final answer. You see that [latex]\large{{{14} \over 2} = 7}[/latex].
Example 5: Simplify by rationalizing the denominator of [latex]\large{{{6 – \sqrt 5 } \over {\sqrt 8 }}}[/latex].
This time the numerator contains a binomial. There’s really no difference in the approach because the denominator is still a monomial. We will multiply the original fraction by the denominator, [latex]\sqrt 8 [/latex].
Make sure to distribute [latex]\sqrt 8 [/latex] into the terms inside the parenthesis.
![6-[sqrt(5)]/sqrt(8)={6-[sqrt(8)]-sqrt(40)}/8](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex5a.png)
The numerator can be further simplified because the radicands have perfect square factors. Observe that [latex]8 = 4 \times 2[/latex] and [latex]40 = 4 \times 10[/latex] where the factor [latex]4\left( {4 = {2^2}} \right)[/latex] is a perfect square number.
![6-[sqrt(5)]/sqrt(8) = {(6)[sqrt(2)]-sqrt(10)/4](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex5b.png)
Example 6: Rationalize [latex]\large{{2 \over {3 + \sqrt 3 }}}[/latex].
This problem is a little bit different because the denominator is now a binomial, containing two terms. To get rid of the radical in the denominator, we are going to multiply the top and bottom by the conjugate of the given denominator.
How do we get the conjugate of the denominator? Take the same denominator but switch the middle sign.
![3+[sqrt(3)] becomes 3-[sqrt(3)]](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex6a.png)
The middle sign of the original denominator switches from positive to negative. Our choice of multiplier that can rationalize the denominator is [latex]\large{{{3 – \sqrt 3 } \over {3 – \sqrt 3 }}}[/latex].
Here goes our solution.
![2/{3+[sqrt(3)]} = {3- [sqrt(3)]}/3](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex6b.png)
Example 7: Rationalize [latex]\large{{3 \over {2 – \sqrt 2 }}}[/latex].
The denominator has a negative sign in the middle which makes the conjugate to have a positive middle sign.
![{2-[sqrt(2)]} becomes {2+[sqrt(2)]}](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex7a.png)
The multiplier to use in order to rationalize the denominator is
![multiply by a fraction that is equal to 1. in this case, conjugate / conjugate = [2+sqrt(2)]/[2+sqrt(2)]](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex7b.png)
Here goes our solution.
![this radical expression is more challenging to rationalize because the denominator is a difference of an integer and an irrational number. therefore, to rationalize [3/(2-sqrt2)] * [2+sqrt(2)]/[2+sqrt(2)] is equal to [6+3*sqrt(2)]/2](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex7c.png)
No common factors between the numerator and denominator, thus this is our final answer.
Example 8: Rationalize [latex]\large{{{\sqrt 7 } \over { – 3 – \sqrt 7 }}}[/latex].
The given denominator is
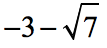
which makes its conjugate to be
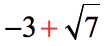
- Given the problem:
![sqrt(7)/[-3-sqrt(7)]](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex8c.png)
- Multiply the numerator and denominator of the original fraction by the conjugate of the denominator.
![sqrt(7)/[-3-sqrt(7)]=sqrt(7)/[-3-sqrt(7)] multiplied to [-3+sqrt(7)]/[-3+sqrt(7)]](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex8-a.png)
- Distribute the numerators, and FOIL the denominators.
![= {[sqrt(7)][-3+sqrt(7)]}/{[-3-sqrt(7)][-3+sqrt(7)]](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex8-b.png)
- The middle terms of the denominator will drop out because they are the “same” in values but opposite in signs.
- Simplify the roots of perfect square numbers, i.e. [latex]\sqrt {49} = 7[/latex].
![= {(-3)[sqrt(7)]+[sqrt(49)}/{9-(3)[sqrt(7)]+(3)[sqrt(7)]-sqrt(49)](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex8-c.png)
- Subtract the values in the denominator, [latex]9 – 7 = 2[/latex].
![= {(-3)[sqrt(7)]+7}/(9-7)](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex8-d.png)
- If possible, reduce the fraction to its lowest terms. It looks like there’s nothing to cancel out between the top and bottom. Therefore, keep this as our final answer.
![= {(-3)[sqrt(7)]+7}/2](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex8-e.png)
Example 9: Rationalize [latex]\large{{{\sqrt 6 – \sqrt 2 } \over {\sqrt 6 + \sqrt 2 }}}[/latex].
Reverse the middle sign of the denominator to obtain its conjugate. That means, the conjugate of [latex]\sqrt 6 + \sqrt 2 [/latex] is [latex]\sqrt 6 – \sqrt 2 [/latex].
- Multiply both the top and bottom by the conjugate.
![{[sqrt(6)]-[sqrt(2)]}/{[sqrt(6)]+[sqrt(2)]} = {[sqrt(6)]-[sqrt(2)]}/{[sqrt(6)]+[sqrt(2)]} multiplied by {[sqrt(6)]-[sqrt(2)]}/{[sqrt(6)]-[sqrt(2)]}](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex9-a.png)
- Apply the FOIL method to expand the binomials.
![= {[sqrt(6)]-[sqrt(2)]}{[sqrt(6)]-[sqrt(2)]}/{[sqrt(6)]+[sqrt(2)]}/{[sqrt(6)]-[sqrt(2)]}](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex9-b.png)
- After expanding using FOIL, the middle terms of the numerator will be added, while the middle terms of the denominator will be canceled.
![= [sqrt(36)-sqrt(12)-sqrt(12)+sqrt(4)]/[sqrt(36)-sqrt(12)+sqrt(12)-sqrt(4)](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex9-c.png)
- Simplify the roots of perfect square numbers in every opportunity
- Add or subtract the whole numbers that come out after getting the square root of perfect square numbers.
![= {6-[sqrt(12)]+2}/(6-2)](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex9-d.png)
- At this point, simplify
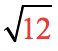
Remember to break it down as a product wherein one of its factors is a perfect square number.
![= [8-sqrt(12)]/4](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex9-e.png)
- Obviously, [latex]12 = 4 \times 3[/latex]. This is a perfect choice of factors since the number [latex]4[/latex] is a perfect square.
![[8-2√(4×3)]/4](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex9f.png)
- Rewrite radical [latex]12[/latex] as the product of the radicals of its factors.
![[8-22-√(4)√(3)]/4](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex9g.png)
- We know that the square root of [latex]4[/latex] equals [latex]2[/latex]!
![={8-[2(2)[sqrt(3)]}/4](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex9h.png)
- Simplify by multiplication
![[8-42-√(3)]/4](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex9i.png)
- The numerator has a common factor of [latex]4[/latex]. That implies we could pull out a factor of [latex]4[/latex] outside the parenthesis.
![[4(2-2-√(3)]/4](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex9j.png)
- Cancel common factors between the numerator and denominator
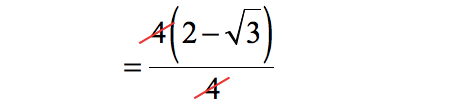
- Write the final answer.
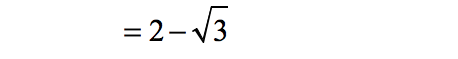
Example 10: Rationalize [latex]\large{{{\sqrt 2 + \sqrt 8 } \over { – \sqrt 2 – \sqrt 8 }}}[/latex].
- Multiply the given fraction, both top and bottom, by the conjugate of the denominator.
![{[sqrt(2)]+[sqrt(8)]}/{-[sqrt(2)]-[sqrt(8)]} = {[sqrt(2)]+[sqrt(8)]}/{-[sqrt(2)]-[sqrt(8)]} multiplied by {-[sqrt(2)]+[sqrt(8)]}/{-[sqrt(2)]+[sqrt(8)]}](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex10a.png)
- For now, multiply the binomials by placing them side by side.
![{[sqrt(2)]+[sqrt(8)]} x {-[sqrt(2)]-[sqrt(8)]}/{-[sqrt(2)]-[sqrt(8)]} x {-[sqrt(2)]-[sqrt(8)]}](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex10b.png)
- Expand the binomials using the FOIL method.
- Cancel out terms that are the “same” but opposite in signs.
![= {-[sqrt(4)]+[sqrt(16)]-[sqrt(16)]+[sqrt(64)]}/{-[sqrt(4)]-[sqrt(16)]+[sqrt(16)]-[sqrt(64)]}](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex10c.png)
- Get the exact values of the square roots of perfect square numbers.
![= {-[sqrt(4)]+[sqrt(64)]}/ {-[sqrt(4)]-[sqrt(64)]}](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex10d.png)
- Perform the required arithmetic operations in both numerator and denominator.
![= [(-2)+8]/(2-8)](https://www.chilimath.com/wp-content/uploads/2018/12/ratdenom-ex10e.png)
- Cancel out common factors. The numerator and denominator is both divisible by [latex]6[/latex].
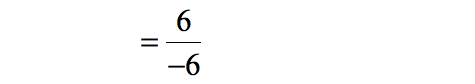
- Write the final answer.

You may also be interested in these related math lessons or tutorials:
Solving Radical Equations
Simplifying Radical Expressions
Adding and Subtracting Radical Expressions
Multiplying Radical Expressions
