FOIL Method

FOIL (the acronym for first, outer, inner and last) method is an efficient way of remembering how to multiply two binomials in a very organized manner.

The word FOIL is an acronym that stands for:

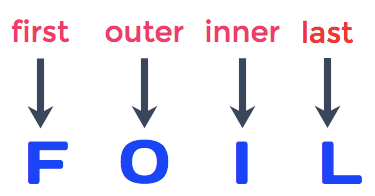
The acronym FOIL stands for first, outer, inner and last.

To put this in perspective, suppose we want to multiply two arbitrary binomials, \left( {a + b} \right)\left( {c + d} \right) 

  • The first means that we multiply the terms which occur in the first position of each binomial.
product of the First Terms is a times c, or ac
  • The outer means that we multiply the terms which are located in both ends (outermost) of the two binomials when written side-by-side.
product of the Outer Terms is a times d, or ad
  • The inner means that we multiply the middle two terms of the binomials when written side-by-side.
product of the Inner Terms is b times c, or bc
  • The last means that we multiply the terms which occur in the last position of each binomial.
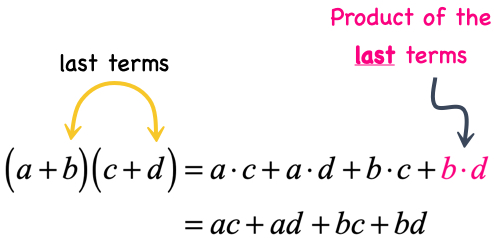
product of the Last Terms is b times d, or bd
  • After obtaining the four (4) partial products coming from the first, outer, inner and last, we simply add them together to get the final answer.

Examples of How to Multiply Binomials using the FOIL Method

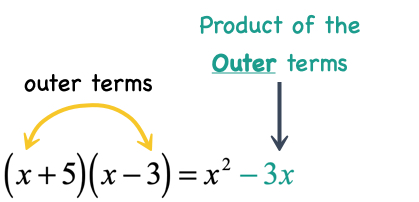
Example 1: Multiply the binomials \left( {x + 5} \right)\left( {x - 3} \right) using the FOIL Method.

  • Multiply the pair of terms coming from the first position of each binomial.
first terms product is x^2
  • Multiply the outer terms when the two binomials are written side-by-side.
outer terms product is -3x
  • Multiply the inner terms when the two binomials are written side-by-side.
inner terms product is 5x
  • Multiply the pair of terms coming from the last position of each binomial.
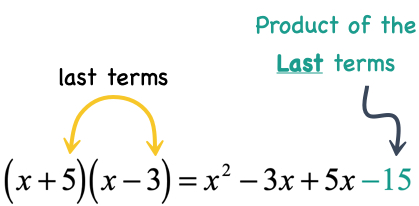
last terms product is -15
  • Finally, simplify by combining like terms. I see that we can combine the two middle terms with variable x.
(x+5) times (x-3) = x^2+2x-15

Example 2: Multiply the binomials \left( {3x - 7} \right)\left( {2x + 1} \right) using the FOIL Method.

If the first presentation on how to multiply binomials using FOIL doesn’t make sense yet. Let me show a different way. The idea is to expose you to different ways on how to address the same type of problem with a different approach.

  • Multiply the first terms
3x multiplied to 2x equals 6x^2
  • Multiply the outer terms
3x times 1 equals 3x
  • Multiply the inner terms
-7 times 2x equals -14x
  • Multiply the last terms
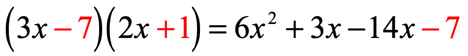
-7 times 1 equals -7

After applying the FOIL, we arrive at this polynomial which we can simplify by combining similar terms. The two middle x-terms can be subtracted to get a single value.

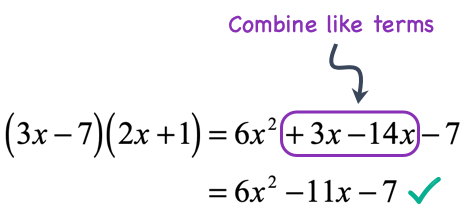
combine the like or similar terms in the middle which are 3x and -14x. (3x) plus negative (14x) is equal to -11x

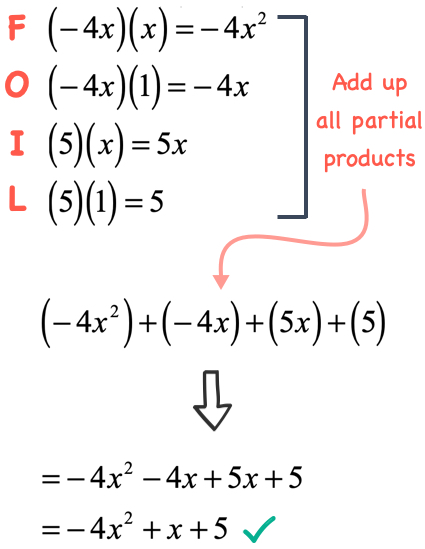
Example 3: Multiply the binomials \left( { - \,4x + 5} \right)\left( {x + 1} \right) using the FOIL Method.

Another way of doing this is to list the four partial products, and then add them together to get the answer.

  • Multiply the first terms
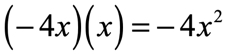
(-4x)(x)=-4x^2
  • Multiply the outer terms
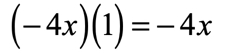
(-4x)(1)=-4x
  • Multiply the inner terms
(5)(x)=5x
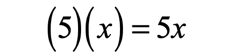
  • Multiply the last terms
(5)*(1)=5

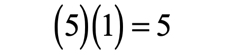
Get the sum of the partial products, and then combine similar terms.

(-4x^2)+(-4x)+(5x)+(5) = -4x^2+x+5

Example 4: Multiply the binomials \left( { - \,7x - 3} \right)\left( { - \,2x + 8} \right) using the FOIL Method.

Solution:

  • Multiply the first terms
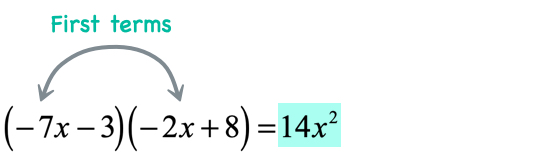
negative seven x times negative two x is equal to fourteen x squared
  • Multiply the outer terms
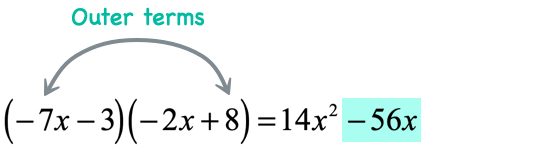
negative seven x multiplied to 8 is equal to negative fifty-six x
  • Multiply the inner terms
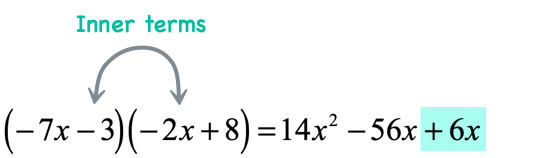
negative three multiplied to negative two x is equal to six x
  • Multiply the last terms
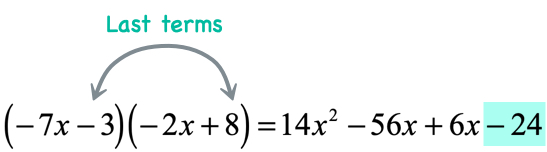
negative three multiplied to eight is equal to negative twenty-four

Finally, combine like terms to finish this off!

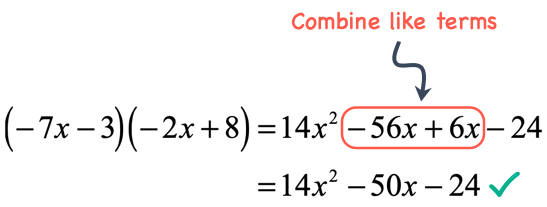
final answer after multiplying the two binomials is 14x^2-50x-24

Example 5: Multiply the binomials \left( { - \,x - 1} \right)\left( { - \,x + 1} \right).

Solution:

  • Multiply the first terms
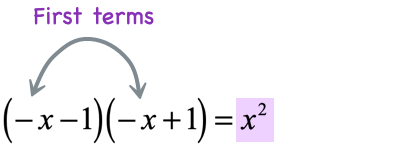
first times first = x^2
  • Multiply the outer terms
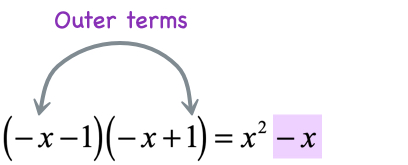
outer terms = -x
  • Multiply the inner terms
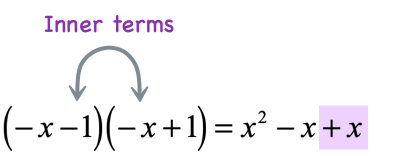
inner = x
  • Multiply the last terms
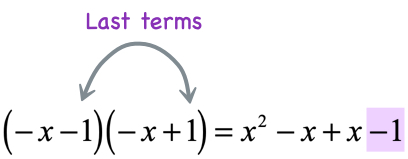
last times last = -1

Notice that the middle two terms cancel each other out!

x^2-1

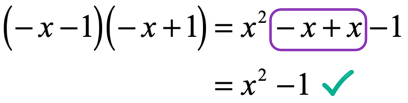
Example 6: Multiply the binomials \left( {6x + 5} \right)\left( {5x + 3} \right).

Solution:

  • Product of the first terms
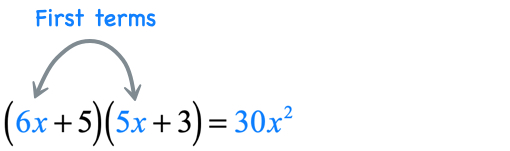
6x*5x = 30x^2
  • Product of the outer terms
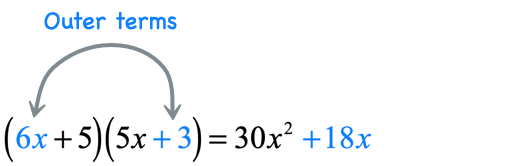
6x*3 = 18x
  • Product of the inner terms
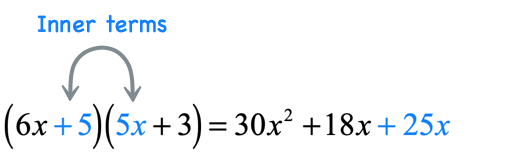
5*5x = 25x
  • Product of the last terms
5*3 = +15

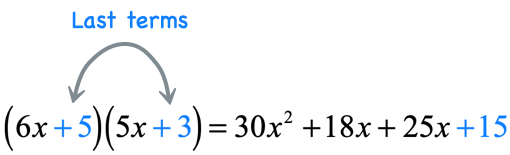
Add the two middle x-terms, and we are done!

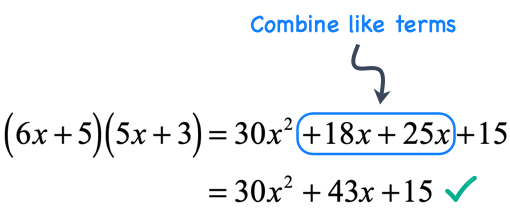
30*x^2+43*x+15

Example 7: Multiply the binomials \left( {x - 12} \right)\left( {2x + 1} \right).

Solution:

  • Product of the first terms
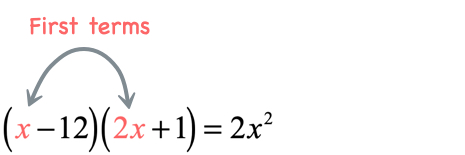
x times 2x = 2x^2
  • Product of the outer terms
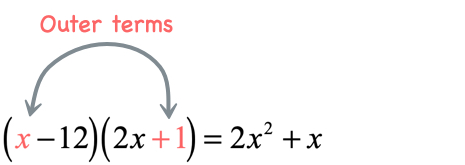
x times 1 = x
  • Product of the inner terms
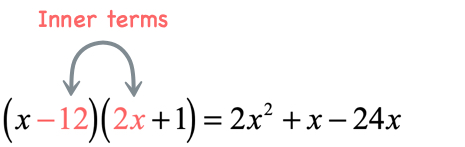
-12 times 2x = -24x
  • Product of the last terms
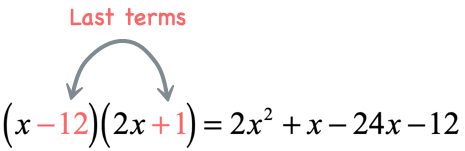
-12 times +1 = -12

After expanding the binomials, combine like terms to get the final answer!

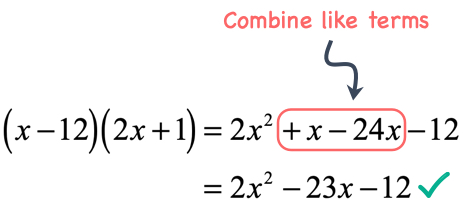
2x^2 minus 23x minus 12

Example 8: Multiply the binomials \left( { - \,10x - 6} \right)\left( {4x - 7} \right).

Solution:

  • Multiply the first terms
-40x^2
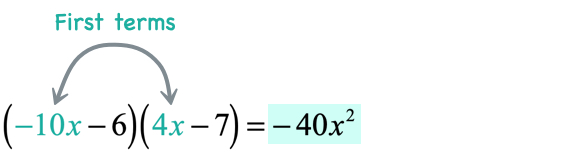
  • Multiply the outer terms
70x
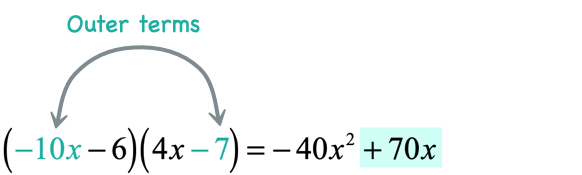
  • Multiply the inner terms
-24x
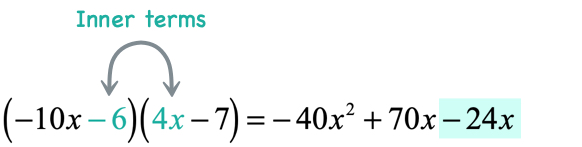
  • Multiply the last terms
42

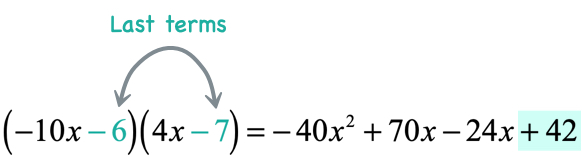
After distributing the terms of the two binomials using the FOIL method, combine like terms to get the final answer.

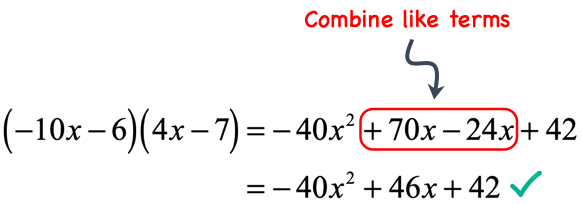
-40x^2+46x+42

You might also be interested in:

Adding and Subtracting Polynomials
Dividing Polynomials using Long Division Method
Dividing Polynomials using Synthetic Division Method
Multiplying Polynomials