Adding and Subtracting Polynomials
The basic component of a polynomial is a monomial. When we add or subtract polynomials, we are actually dealing with the addition and subtraction of individual monomials that are similar or alike.
What is a Monomial?
A monomial can be a single number, a single variable, or the product of a number and one or more variables that contain whole number exponents.
This means that the exponents are neither negative nor fractional.
Examples:
- [latex]7[/latex]
- [latex]y[/latex]
- [latex]2x[/latex]
- [latex] – \,9xy[/latex]
- [latex] – \,4x{y^2}[/latex]
- [latex]10{x^2}{y^3}{z^4}[/latex]
- [latex]{3 \over 4}{k^5}{m^2}h{r^{12}}[/latex]
So now we are ready to define what a polynomial is.
What is a Polynomial?
A polynomial can be a single monomial or a combination of two or more monomials connected by the operations of addition and subtraction.
Examples:
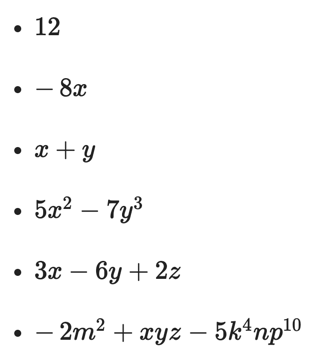
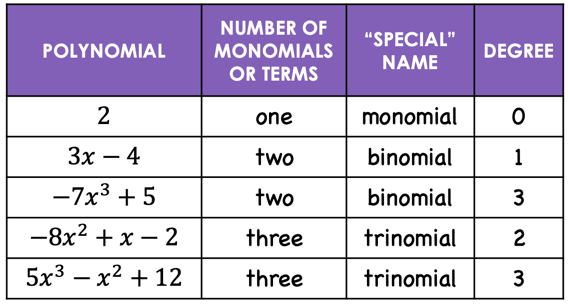
A polynomial has “special” names depending on the number of monomials or terms in the expression. More so, the degree of a polynomial with a single variable is determined by the largest whole number exponent among the variables.
For example:
Examples of How to Add and Subtract Polynomials
Example 1: Simplify by adding the polynomial expressions
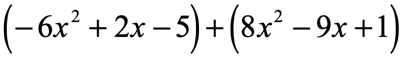
The key in both adding and subtracting polynomials is to make sure that each polynomial is arranged in standard form. It means that the powers of the variables are in decreasing order from left to right.
Observe that each polynomial in this example is already in standard form, so we no longer need to perform that preliminary step.
Now, there are two ways we can proceed from here.
- First, we can add this the “usual” way, that is, add them horizontally.
I suggest that you first group similar terms in parenthesis before performing addition.
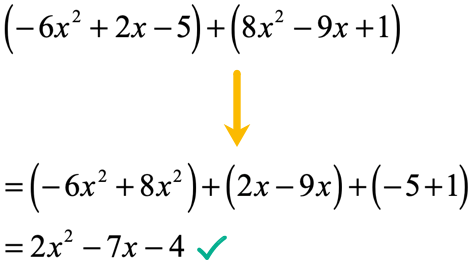
- Another way of simplifying this is to add them vertically.
Place the similar terms in the same column before performing addition.
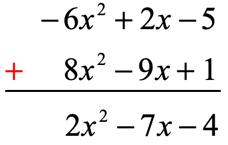
As you can see, the answers in both methods came out to be the same!
Example 2: Simplify by adding the polynomial expressions
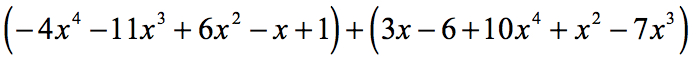
Notice that the first polynomial is already in the standard form because the exponents are in decreasing order. However, the second polynomial is not! We must first rearrange the powers of [latex]x[/latex] in decreasing order from left to right.
- Then add them horizontally…
Similar or like terms are placed in the same parenthesis.
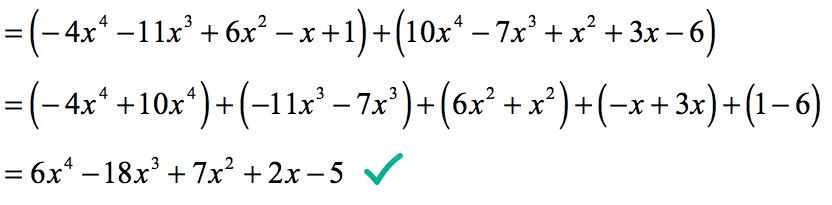
- Or add them vertically…
Similar or like terms are placed in the same column before performing the addition operation.
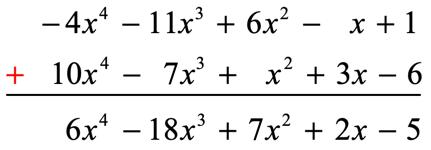
Example 3: Simplify by adding the polynomial expressions
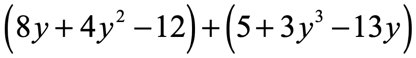
Solution:
We are given two trinomials to add. But first, we have to “fix” each one of them by expressing it in standard form.
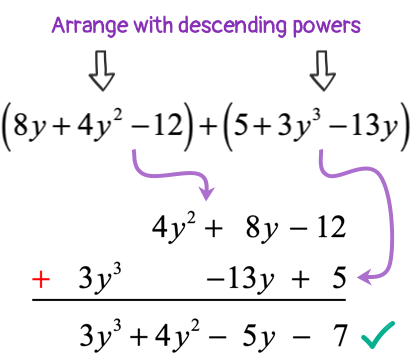
Add only similar terms. Notice that the [latex]y[/latex]
- Adding Polynomials – Horizontally

Let’s check our work if the answer comes out the same when we add them vertically.
- Adding Polynomials – Vertically
Example 4: Simplify by adding the polynomial expressions
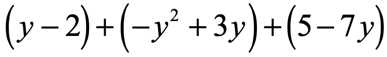
Solution:
Let’s add the polynomials above vertically. Align like terms in the same column then proceed with polynomial addition as usual.
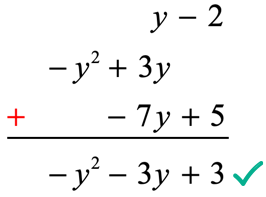
Example 5: Simplify by subtracting the polynomial expressions
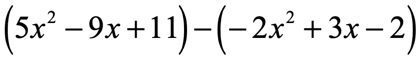
Subtracting polynomials is as easy as changing the operation to normal addition. However, always remember to also switch the signs of the polynomial being subtracted.
This is how it looks when we rewrite the original problem from subtraction to addition with some changes on the signs of each term of the second polynomial.
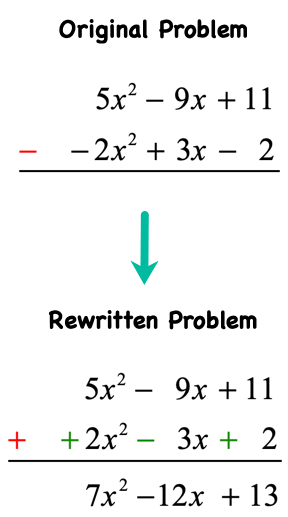
Original Problem

Rewritten Problem

- The original subtraction operation is replaced by addition.
- The second polynomial is “tweaked” by reversing the original sign of each term.
At this point, we can proceed with our normal addition of polynomials. Make sure that similar terms are grouped together inside a parenthesis.
Subtracting Polynomials – Horizontally
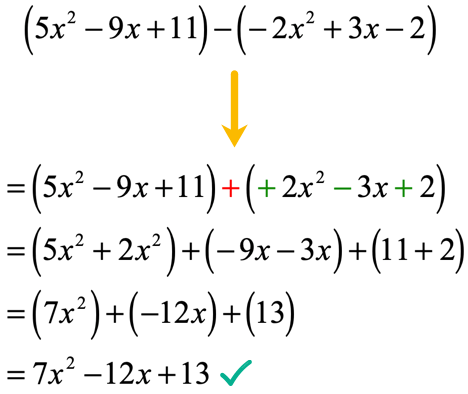
Subtracting Polynomials – Vertically
We can also subtract the polynomials in a vertical way. First, convert the original subtraction problem into its addition problem counterpart as shown by the green arrow. Make sure to align similar terms in a column before performing addition.
Example 6: Simplify by subtracting the polynomial expressions
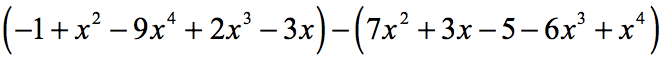
The two polynomials that we are about to subtract are not in standard form. Begin by rearranging the powers of variable [latex]x[/latex] in decreasing order. Change the operation from subtraction to addition, align similar terms, and simplify to get the final answer.
Transform each polynomial in standard form

Subtract by switching the signs of the second polynomial, and then add them together.

Example 7: Simplify by subtracting the polynomial expressions
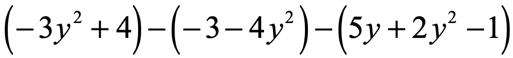
In this problem, we are going to perform the subtraction operation twice.

That means we also need to flip the signs of the two polynomials which are the second and third.
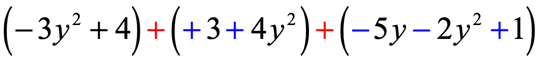
Perform regular addition using columns of similar or like terms.
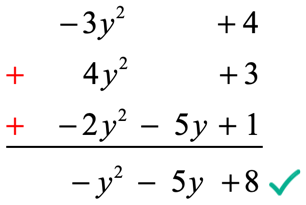
Example 8: Simplify by adding and subtracting the polynomials
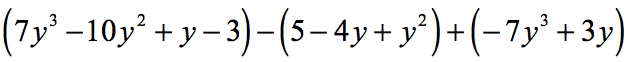
Solution:
Rewrite each polynomial in the standard format. Replace subtraction with addition while reversing the signs of the polynomial in question. Finally, organize like or similar terms in the same column and proceed with regular addition.
Adding the polynomials vertically, we have…
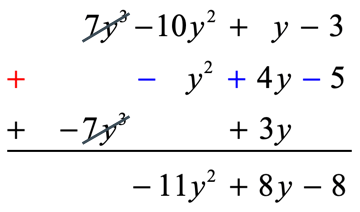
Example 9: Simplify by adding and subtracting the polynomials
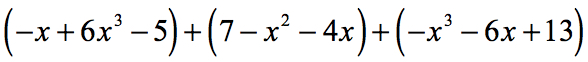
Solution:
Rewrite each polynomial in the standard format. Replace subtraction with addition while reversing the signs of the polynomial in question. Finally, organize like or similar terms in the same column and proceed with regular addition.
If we add the polynomials vertically, we have…
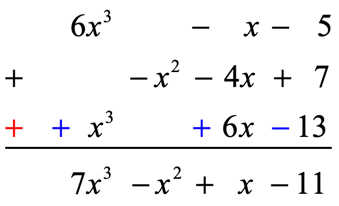
You may also be interested in these related math lessons or tutorials:
Dividing Polynomials using Long Division Method
Dividing Polynomials using Synthetic Division Method
Multiplying Binomials using FOIL Method
Multiplying Polynomials
