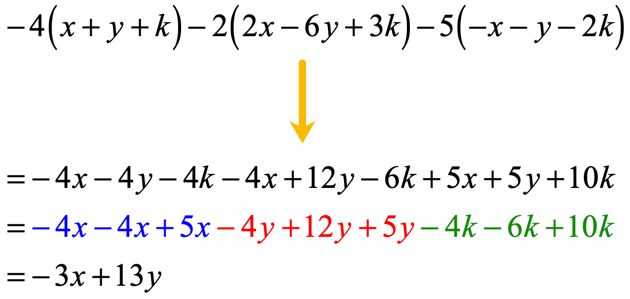How to Combine Like Terms

When you were learning how to add or subtract numbers, you may have started with similar objects such as fruits. For instance, if there are three apples in a box and you place two more, how many apples are there? Obviously, it is possible to add them together because the fruits involved are of the same kind.

In algebra, this idea of adding apples can be represented using the simple equation below. Notice that we are able to combine the two terms, [latex]3a[/latex] and [latex]2a[/latex] because they have the same variable part which is [latex]a[/latex]. We say that they are similar or like terms.

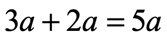
Now, how about if we have apples and bananas? Can we simply add them too? The answer is NO. Apples and bananas are two different kinds of fruits, so putting them together is just creating a pile of fruits. It is not possible to say that “[latex]3[/latex] apples plus [latex]2[/latex] bananas is equal to [latex]5[/latex] applebananas“. There’s no such thing!

---

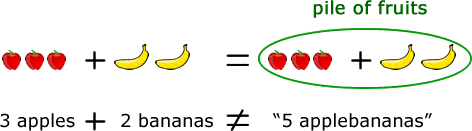
Examples of How to Combine Like Terms with or without the Distributive Property

Now, let’s take a look at some examples!

Example 1: Simplify the expression below by combining like terms.

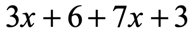
There are four terms in this algebraic expression. Two terms with similar [latex]x[/latex]-variables, [latex]3x[/latex] and [latex]7x[/latex], and two constant terms which are [latex]6[/latex] and [latex]3[/latex]. Since they are like terms, we can definitely combine them using the required operation.

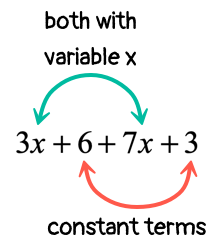
I would place similar terms side by side first before combining them together.

---

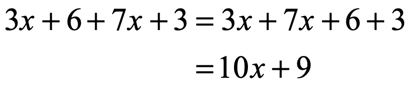
Example 2: Simplify the expression below by combining like terms.

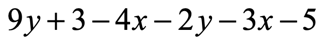
I see that we have three kinds of similar terms that can be combined which are the [latex]y[/latex]-terms, [latex]x[/latex]-terms, and constant terms.

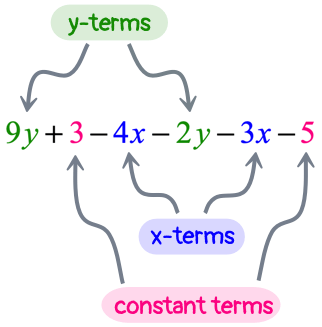
Let’s rearrange the expression such that similar terms are adjacent or close to each other. This allows us to have a “laser” focus on which terms to add or subtract.

---

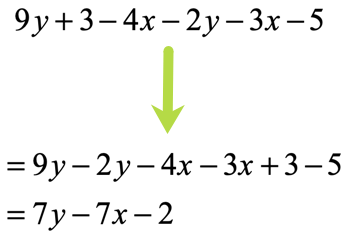
Example 3: Simplify the expression below by combining like terms.

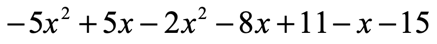
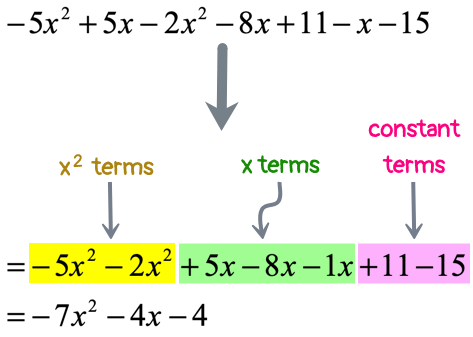
Don’t assume that terms with the same variable are automatically like or similar terms. Remember that each variable must also have a matching exponent value. Be careful to distinguish that [latex]{x^2}[/latex] and [latex]x[/latex] are not like terms because the first [latex]x[/latex]-variable has an exponent of [latex]2[/latex], while the second is [latex]1[/latex].

In fact we have three distinct groups of like terms here; namely, terms with [latex]{x^2}[/latex], [latex]x[/latex], and the pure numbers (constants). Move around the terms in the expression such that like terms are placed side by side before we combine them either by adding or subtracting. Don’t forget also to keep the original signs in front of each term when you move them around.

Just a quick note, the term [latex] – x[/latex] is understood to have a coefficient of [latex] – 1[/latex]. Hence, [latex] – x = – 1x[/latex].

---

Example 4: Simplify the expression below by combining like terms.

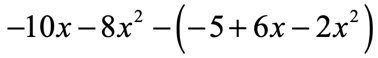
We can’t combine like terms just yet because of the presence of a parenthesis. We need to somehow get rid of that before proceeding with the usual steps. If you are not sure how to start this out, remember to replace that minus symbol in front of the parenthesis by [latex] – 1[/latex].

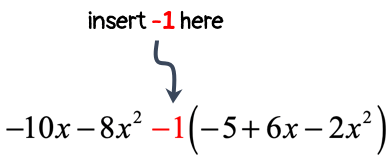
The next step is to distribute that [latex] – 1[/latex] through the terms inside the parenthesis. By doing so, two things happen! The parenthesis is eliminated, and the terms inside the parenthesis will switch signs.

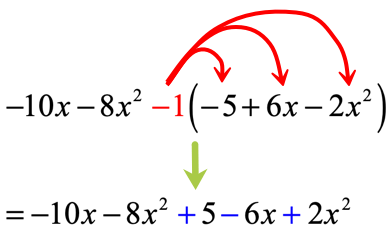
Now that the parenthesis is gone, we can proceed with steps in combining like terms. Group together similar terms, and then add or subtract them whatever operation is required.

---

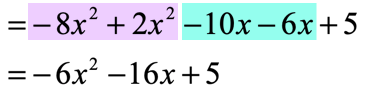
Example 5: Simplify the expression below.

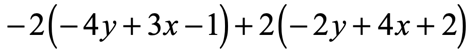
I hope you see this one coming! This is an “upgrade” to the previous problem because this time around, the expression contains two parentheses. It should be clear at this point that we should eliminate them before we can move forward.

We begin by distributing the constant terms into the terms inside the parenthesis.

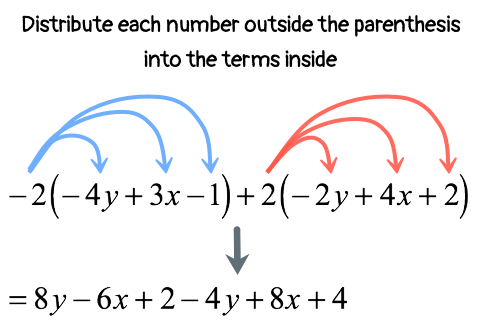
Then, rearrange the terms so that similar terms are clustered together. Finally, combine like terms by adding or subtracting whichever is required.

---

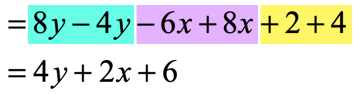
Example 6: Simplify the expression below.

This is an example of nested grouping symbols. Observe that there is a parenthesis inside the main square bracket. We will simplify the inner parenthesis first and then work ourselves outward. Let’s simplify this step by step.

• Step 1: Combine the [latex]x[/latex]-variables within the inner parenthesis.

• Step 2: Distribute the constant [latex]2[/latex] into the terms of the inner parenthesis.

• Step 3: Combine like terms as much as possible inside the square bracket symbol. Identify like terms first before combining.

• Step 4: Distribute the constant [latex]- 3[/latex] through the terms inside the square bracket to get rid of it.

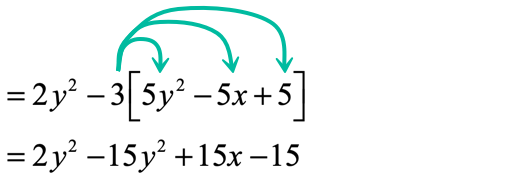
• Step 5: Finish this off by combining like terms again that show up after eliminating the square bracket symbol.

---

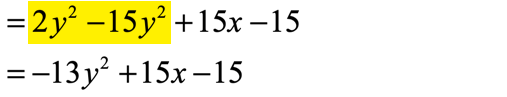
Example 7: Simplify the expression below.

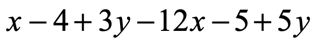
Solution:

To simplify this expression, place side by side the [latex]x[/latex] terms, [latex]y[/latex] terms, and constant terms. Then, proceed with regular addition or subtraction of like terms.

---

Example 8: Simplify the expression below.

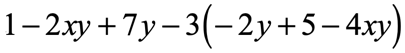
Solution:

---

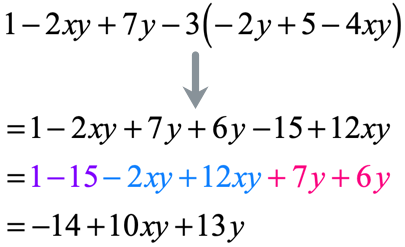
Example 9: Simplify the expression below.

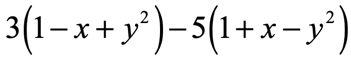
Solution:

First, distribute the constant terms, [latex]3[/latex] and [latex]- 5[/latex] into the terms inside the parenthesis. Next, combine similar terms together then add or subtract as required.

---

Example 10: Simplify the expression below.

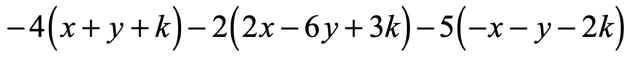
Solution: