How to Multiply Radical Expressions
In this lesson, we are only going to deal with square roots only which is a specific type of radical expression with an index of [latex]\color{red}2[/latex]. If you see a radical symbol without an index explicitly written, it is understood to have an index of [latex]\color{red}2[/latex].
Below are the basic rules in multiplying radical expressions.
Basic Rule on How to Multiply Radical Expressions
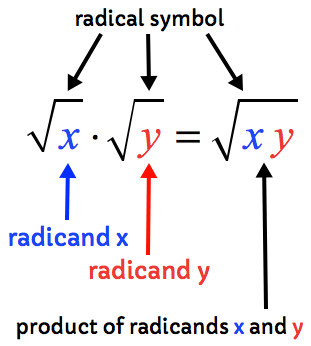
A radicand is a term inside the square root. We multiply radicals by multiplying their radicands together while keeping their product under the same radical symbol. What happens then if the radical expressions have numbers that are located outside?
We just need to tweak the formula above. But the key idea is that the product of numbers located outside the radical symbols remains outside as well.
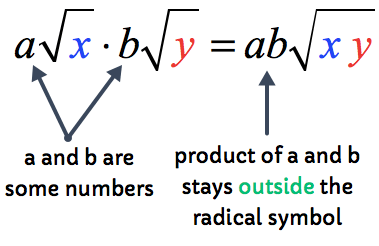
Let’s go over some examples to see how these two basic rules are applied.
Examples of How to Multiply Radical Expressions
Example 1: Simplify by multiplying.
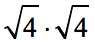
Multiply the radicands while keeping the product inside the square root.
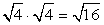
The product is a perfect square since 16 = 4 · 4 = 42, which means that the square root of [latex]\color{blue}16[/latex] is just a whole number.
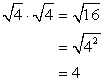
Example 2: Simplify by multiplying.
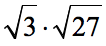
It is okay to multiply the numbers as long as they are both found under the radical symbol. After the multiplication of the radicands, observe if it is possible to simplify further.
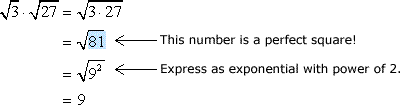
Example 3: Simplify by multiplying.
![√(2) [√(2) - 3]](https://www.chilimath.com/wp-content/uploads/2019/01/ex3.png)
Take the number outside the parenthesis and distribute it to the numbers inside. We are just applying the distributive property of multiplication.
![√2[(√2)-3]=(√2)(√2)-(√2)(3)](https://www.chilimath.com/wp-content/uploads/2017/06/ex3_1.gif)
Next, proceed with the regular multiplication of radicals. Be careful here though. You can only multiply numbers that are inside the radical symbols. In the same manner, you can only numbers that are outside of the radical symbols.
When multiplying a number inside and a number outside the radical symbol, simply place them side by side.
![√2[(√2)-3]=2-3√2](https://www.chilimath.com/wp-content/uploads/2017/06/ex3_2.gif)
Example 4: Simplify by multiplying.
![-3√(12) [5√(3) - 4√(6)]](https://www.chilimath.com/wp-content/uploads/2019/01/ex4.png)
Similar to Example 3, we are going to distribute the number outside the parenthesis to the numbers inside. But make sure to multiply the numbers only if their “locations” are the same. That is, multiply the numbers outside the radical symbols independent from the numbers inside the radical symbols.
![Multiply [(-3)(5)] and [(-3)(4)] then multiply [(√12)(√3)] and [(√12)(√6)].](https://www.chilimath.com/wp-content/uploads/2017/06/ex4_1.gif)
From here, I just need to simplify the products.
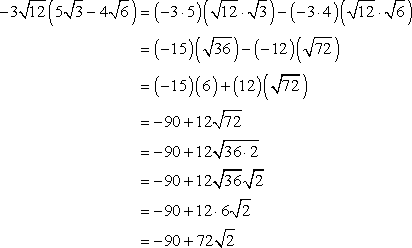
Example 5: Simplify by multiplying.
![-2√(7) [-5-3√(7)]](https://www.chilimath.com/wp-content/uploads/2019/01/ex5.png)
Solution:
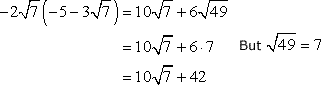
Example 6: Simplify by multiplying two binomials with radical terms.
![[1-√(5)] [1+√(5)]](https://www.chilimath.com/wp-content/uploads/2019/01/ex6.png)
This problem requires us to multiply two binomials that contain radical terms. Apply the FOIL method to simplify.
- F: Multiply the first terms.
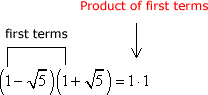
- O: Multiply the outer terms.
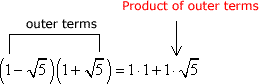
- I: Multiply the inner terms.
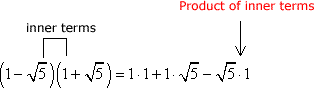
- L: Multiply the last terms.
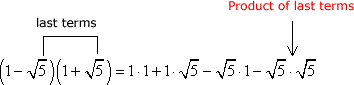
After applying the distributive property using the FOIL method, I will simplify them as usual.
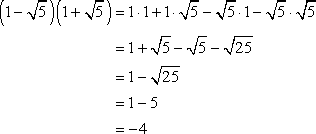
Example 7: Simplify by multiplying two binomials with radical terms.
![[3√(6)-6] [3√(6)+6]](https://www.chilimath.com/wp-content/uploads/2019/01/ex7.png)
Just like in our previous example, let’s apply the FOIL method to simplify the product of two binomials.
- F: Multiply the first terms.
![[(3√6)-6][(3√6)+6]=(3√6)(3√6)](https://www.chilimath.com/wp-content/uploads/2017/06/ex7_s1.gif)
- O: Multiply the outer terms.
![[(3√6)-6][(3√6)+6]=(3√6)(3√6)+(3√6)(6)](https://www.chilimath.com/wp-content/uploads/2017/06/ex7_s2.gif)
- I: Multiply the inner terms.
![[(3√6)-6][(3√6)+6]=(3√6)(3√6)+(3√6)(6)-6(3√6)](https://www.chilimath.com/wp-content/uploads/2017/06/ex7_s3.gif)
- L: Multiply the last terms.
![[(3√6)-6][(3√6)+6]=(3√6)(3√6)+(3√6)(6)-6(3√6)-(6)(6)](https://www.chilimath.com/wp-content/uploads/2017/06/ex7_s4.gif)
From this point, simplify as usual. Notice that the middle two terms cancel each other out.
![[(3√6)-6][(3√6)+6]=18](https://www.chilimath.com/wp-content/uploads/2017/06/ex7_s5.gif)
Example 8: Simplify by multiplying two binomials with radical terms.
![[-√(5)-1] [-√(5)-1]](https://www.chilimath.com/wp-content/uploads/2019/01/ex8.png)
Let’s solve this step-by-step:
- Multiply together using the FOIL method.
![[(-√5)-1] [(-√5)-1]=(√5)(-√5)-[(√5)(-1)]-[(1)(-√5)]-[(1)(-1)]](https://www.chilimath.com/wp-content/uploads/2017/06/ex8_r1_c1.gif)
- Simplify the product.
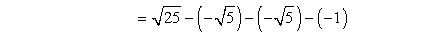
- Simplify the signs.
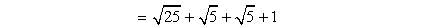
- Add similar radicals.
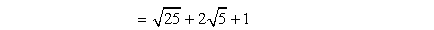
- Simplify the square root of [latex]25[/latex].
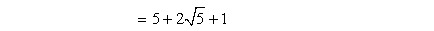
- Add the numbers without radical symbols
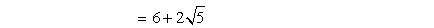
Example 9: Simplify by multiplying two binomials with radical terms.
![[3√(12)-2√(3)] [√(2)+√(3)]](https://www.chilimath.com/wp-content/uploads/2019/01/ex9.png)
Let’s solve this step-by-step:
- Expand the product of binomials using FOIL.
![[(3√12)-(2√(3)] [(√2)+(√3)]=(3√12)(√2)+(3√12)(√3)-(2√3)(√2)-(2√3)(√3)](https://www.chilimath.com/wp-content/uploads/2017/06/ex9s_r1_c1.gif)
- Get the square roots of perfect square numbers which are [latex]\color{red}36[/latex] and [latex]\color{red}9[/latex].
![= (3√24)+[3(6)]-(2√6)-[2(3)]](https://www.chilimath.com/wp-content/uploads/2017/06/ex9s_r2_c1.gif)
- Find a perfect square factor for 24.
- Break it down as a product of square roots.
- Simplify the square root of [latex]4[/latex].
![=[(3√4)(√6)]+18-(2√6)-6](https://www.chilimath.com/wp-content/uploads/2017/06/ex9s_r3_c1.gif)
- Subtract the similar radicals, and subtract also the numbers without radical symbols.
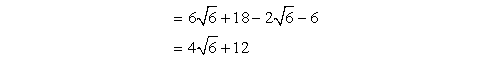
Example 10: Simplify by multiplying.
![[-√(2)-3√(2)] [2+√(8)]](https://www.chilimath.com/wp-content/uploads/2019/01/ex10.png)
We are going to multiply these binomials using the “matrix method”. Write the terms of the first binomial (in blue) in the left-most column, and write the terms of the second binomial (in red) on the top row.
Multiply the numbers of the corresponding grids. See the animation below.
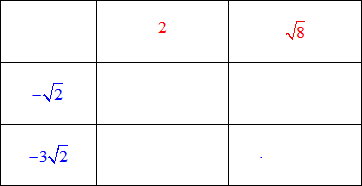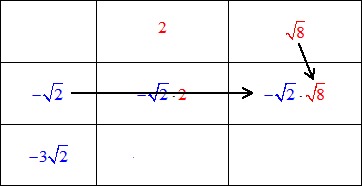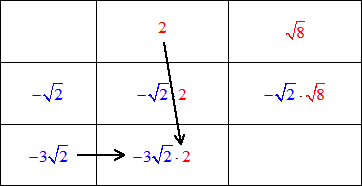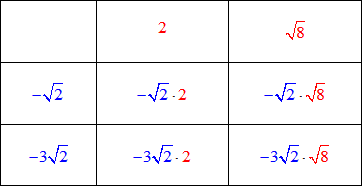
Next, simplify the product inside each grid.
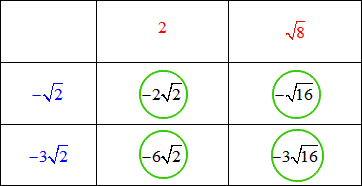
Finally, add all the products in all four grids, and simplify to get the final answer.
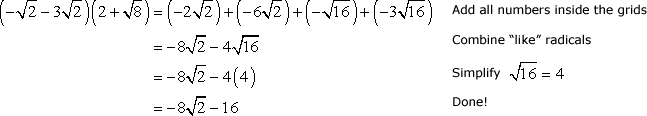
Example 11: Simplify by multiplying.
![[√(3)-√(7)] [√(7)-√(3)]](https://www.chilimath.com/wp-content/uploads/2019/01/example-11.png)
Place the terms of the first binomial in the left-most column, and the terms of the second binomial on the top row. Then multiply the corresponding square grids.
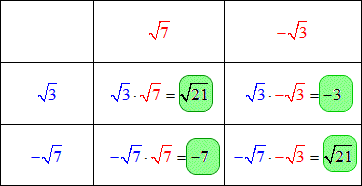
Finally, add the values in the four grids, and simplify as much as possible to get the final answer.

You may also be interested in these related math lessons or tutorials:
Solving Radical Equations
Simplifying Radical Expressions
Adding and Subtracting Radical Expressions
Rationalizing the Denominator
