Adding and Subtracting Radical Expressions
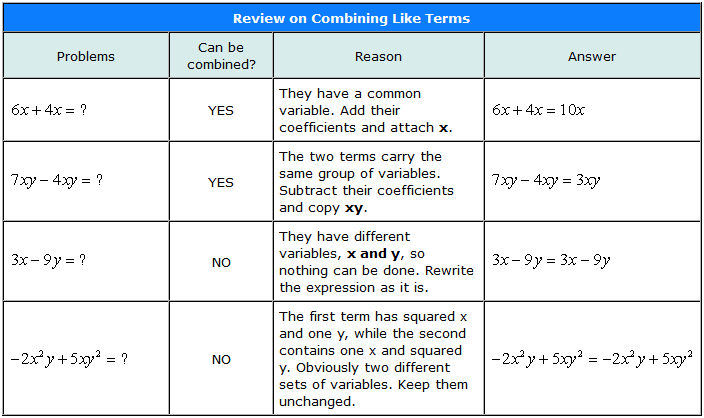
You could probably still remember when your algebra teacher taught you how to combine like terms. The goal is to add or subtract variables as long as they “look” the same. Otherwise, we just have to keep them unchanged. For a quick review, let’s simplify the following algebraic expressions by combining like terms.
Simplifying Algebraic Expressions by Combining Like Terms
Now, just like combining like terms, you can add or subtract radical expressions if they have the same radical component. Since we are only dealing with square roots in this lesson, the only thing we have to worry about is to make sure that the radicand (stuff inside the radical symbol) are similar terms.
Let’s go over some examples to see them in action!
Examples of How to Add and Subtract Radical Expressions
Example 1: Simplify by adding and/or subtracting the radical expressions below.
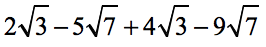
Observe that each of the radicands doesn’t have a perfect square factor. This shows that they are already in their simplest form. The next step is to combine “like” radicals in the same way we combine similar terms.
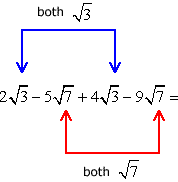
I will rearrange the problem by placing similar radicals side by side to guide me in adding or subtracting appropriate radical expressions correctly. Maybe you can think of this as adding/subtracting the “coefficients” of like radical expressions.
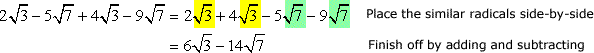
The calculator agrees with our answer.

Example 2: Simplify by adding and/or subtracting the radical expressions below.
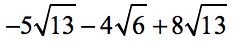
We can combine the two terms with [latex]\sqrt {13}[/latex] . The one with [latex]\sqrt 6[/latex] will simply be carried along because there is nothing we can combine it with.
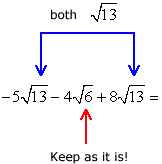
Rearrange the terms such that similar radicals are placed side by side for easy calculation.
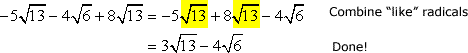
The calculator gives us the same result. Great!

Example 3: Simplify the radical expressions below.
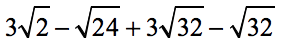
The first thing I would do is combine the obvious similar radicals, which in this case, the expressions with [latex]\sqrt {32}[/latex] .

I realize that the radical [latex]\sqrt 2[/latex] is in its simplest form; however, the two radicals [latex]\sqrt {24}[/latex] and [latex]\sqrt {32}[/latex] need some simplification first. If you need a refresher on how to simplify radical expressions, check out my separate tutorial on simplifying radical expressions.
To simplify radical expressions, the key step is to always find the largest perfect square factor of the given radicand. Next, break them into a product of smaller square roots, and simplify.
You can have something like this table on your scratch paper.
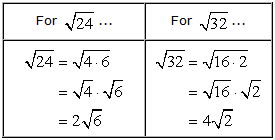
After simplifying the radical expressions in our side calculation, as shown above, we can now proceed as usual.
I will incorporate the simplification of radicals in the overall solution. I use some color coding to help you follow how the radicands are factored out, broken down into smaller radicals and simplified.
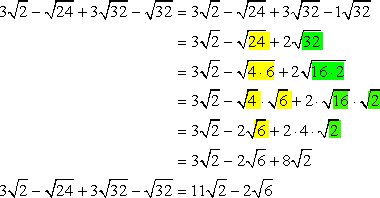
Yep! Our calculator yields the same answer.
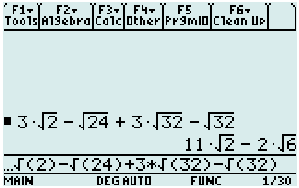
Example 4: Add and subtract the radical expressions below.
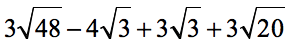
First off, I will combine the radical expressions with [latex]\sqrt 3[/latex].
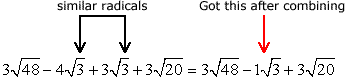
Now, deal with radicands that have perfect square factors. We know that they can be simplified further.
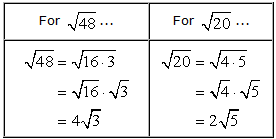
That side calculation above should help us finish our solution.
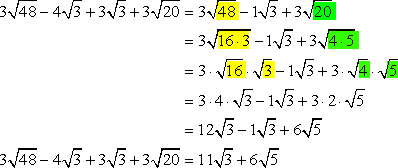
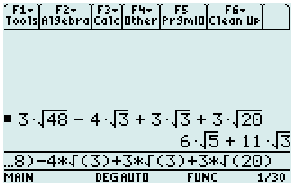
Checking our answer with a calculator, the answer above is correct! Notice that addition is commutative. That means the order of addition does not affect the final value.
Example 5: Add and subtract the radical expressions below.
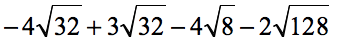
- Combine first the radical expressions with [latex]\sqrt {32}[/latex]
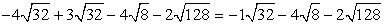
- Break down the radicands with perfect square factors, and simplify. The final answer is reduced to a single radical expression.
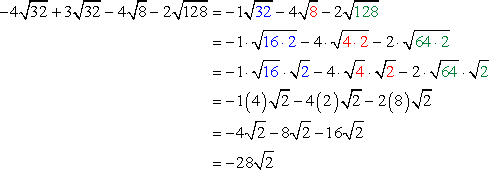
- Calculator check. We got it again!
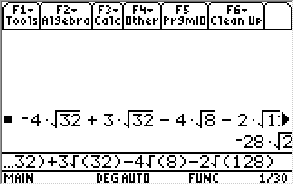
Example 6: Simplify by combining the radical expressions below.
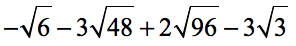
Solution:
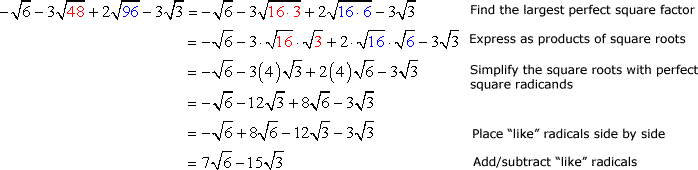
Example 7: Add and subtract to simplify the radical expressions below.
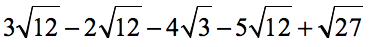
Solution:
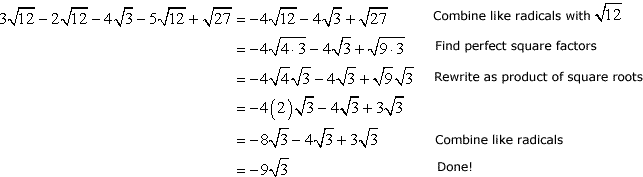
Example 8: Add and subtract to simplify the radical expressions below.
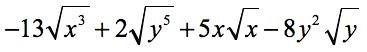
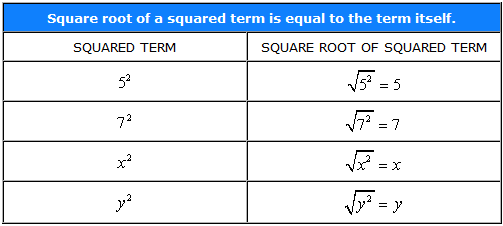
Here, we have variables inside the radical symbol. To simplify this, remember the concept that the square root of a squared term, either numerical or variable, is just the term itself. For quick examples…
Therefore, the approach is to express (as much as possible) each variable raised to some power as products of a variable with an exponent of 2 because this allows us to easily get the square root. Now back to the problem…
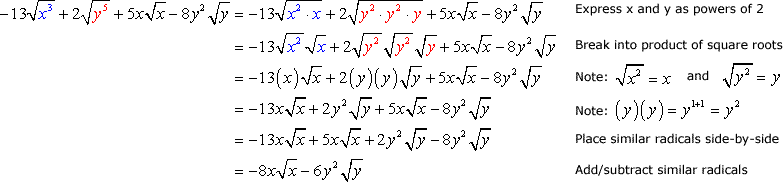
Example 9: Add and subtract to simplify the radical expressions below.
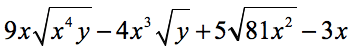
It seems that all radical expressions are different from each other. First, let’s simplify the radicals, and hopefully, something would come out nicely by having “like” radicals that we can add or subtract.
Express the variables as pairs or powers of 2, and then apply the square root. Here we go!
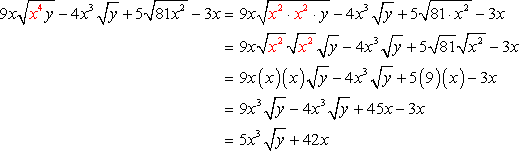
Example 10: Simplify the radical expressions below.
![-3√[(27)(m^3)]+8m√[(12)(m)]-2m√[(3)(m)]](https://www.chilimath.com/wp-content/uploads/2019/01/add-subtract-radicals-example-10.png)
There are no obvious “like” radicals that we can add or subtract. Simplify each radical expression, and observe what we can do from that point.
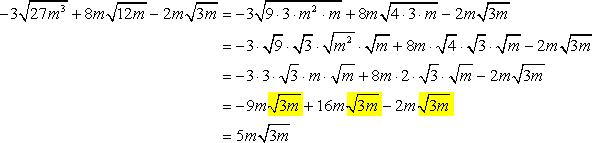
We are able to generate “like” radicals that we can ultimately add or subtract to simplify our final answer.
You may also be interested in these related math lessons or tutorials:
Simplifying Radical Expressions
