How to Solve Multi-Step Equations
The word “multi” means more than two, or many. That’s why solving multi-step equations are more involved than one-step and two-step equations because they require more steps.
The main goal in solving multi-step equations, just like in one-step and two-step equations, is to isolate the unknown variable on one side of the equation while keeping the constant or number on the opposite side.
However, there is no rule on where to keep the variable. It all depends on your preference. The “standard” or usual way is to have it on the left side. But there are cases when it makes more sense to keep it on the right side of the equation.
Since we are dealing with equations, we need to keep in mind that whatever operation we perform on one side must also be applied on the other to keep the equation “balanced”.
This concept of performing the same operation on both sides applies to the four arithmetic operations, namely: addition, subtraction, multiplication, and division. For example, if we add 5 on the left side of the equation we must also add 5 on the right side.
Key steps to remember:
- Get rid of any grouping symbols such as square brackets, parentheses, etc, by applying the Distributive Property of Multiplication over Addition.
- Simplify both sides of the equation, if possible, by combining like terms.
- Decide where you want to keep the variable because that will help you decide where to place the constant.
- Eliminate numbers or variables by applying opposite operations: addition and subtraction are opposite operations as in the case of multiplication and division.
Examples of How to Solve Multi-Step Equations
Example 1: Solve the multi-step equation below.
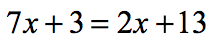
This is a typical problem in multi-step equations where there are variables on both sides. Notice that there is no parenthesis in this equation and no like terms to combine on both sides of the equation.
Clearly, our first step is to decide where to keep or isolate the unknown variable [latex]x[/latex]. Since [latex]7x[/latex] is “larger” than [latex]2x[/latex], then we might as well keep it to the left side. This means we will have to get rid of the [latex]2x[/latex] on the right side. To do that, we need to subtract both sides of the equation by [latex]2x [/latex] because the opposite of [latex]+2x[/latex] is [latex]-2x[/latex].
After doing so, it is nice to see just the variable x on the left side. This implies that we have to move all the constants to the right side by eliminating [latex]+3[/latex] on the left side. The opposite of [latex]+3[/latex] is [latex]-3[/latex], therefore, we will subtract both sides by [latex]3[/latex].
The last step is to isolate the variable [latex]x[/latex] by itself on the left side of the equation. Since [latex]+5[/latex] is multiplying [latex]x[/latex], then its opposite operation is to divide by [latex]+5[/latex]. So, we are going to divide both sides by [latex]5[/latex], and then we are done!
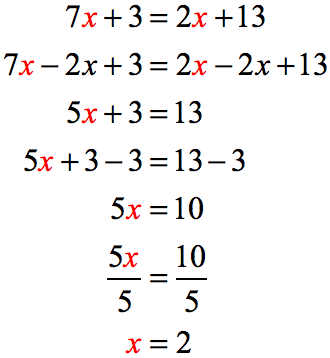
Example 2: Solve the multi-step equation below.
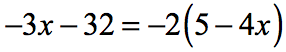
Our very first step should be to get rid of the parenthesis by applying the Distributive Property of Multiplication over Addition. That is, multiply [latex] -2[/latex] inside each term in the parenthesis [latex](5-4x)[/latex].
Now, it is time to decide where to keep the unknown variable [latex]x[/latex]. If you decide to keep the variable on the left side, that is perfectly fine.
However, for practice, let’s try keeping it on the right side. We should arrive at the same answers.
To get rid of the [latex]-3x[/latex] on the left side, we add both sides by [latex]3x[/latex] since the opposite of [latex]-3x[/latex] is [latex]+3x[/latex]. After we simplify by adding both sides by [latex]3x[/latex], we obtain this less messy equation.
It’s nice to see the variable x just on the right side. So, we have to move all the constants to the left side.
Clearly, the [latex]-10[/latex] on the right must be removed. The opposite of [latex]-10[/latex] is [latex]+10[/latex], therefore, we will add both sides by [latex]10[/latex]. The last step is to isolate the variable [latex]x[/latex] by itself on the right side of the equation.
Since [latex]+11[/latex] is multiplying [latex]x[/latex], then its opposite operation is to divide by [latex]+11[/latex]. So, we are going to divide both sides by [latex]11[/latex] and we are done!
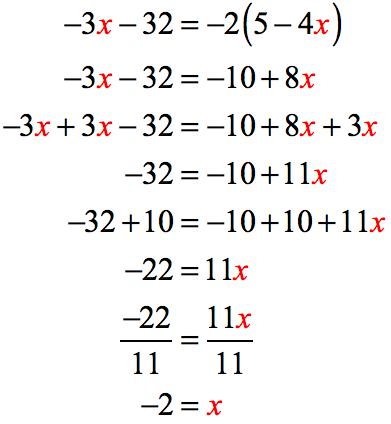
Example 3: Solve the multi-step equation below.
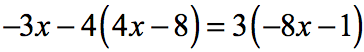
Our first step should be to eliminate the parentheses on BOTH sides of the equation by applying the Distributive property. For the left side, multiply [latex]-4[/latex] inside each term of the parenthesis [latex](4x-8)[/latex] and for the right side, multiply [latex]+3[/latex] inside the parenthesis [latex](-8x-1)[/latex].
Now, before we even decide which side of the equation to isolate the variable, it looks like we have to perform some house cleaning. We need to combine like terms (the x’s) on the left side of the equation.
Again it doesn’t matter which side to isolate the variable being solved. Say, we decided to keep it on the left.
That means we have to get rid of the [latex]-24x[/latex] on the right side. The opposite of [latex]-24x[/latex] is [latex]+24x[/latex] so we are going to add both sides by [latex]24x[/latex].
Next, we have to move all the constants to the right side of the equation. That [latex]+32[/latex] on the left side must go! The opposite of [latex]+32[/latex] is [latex]-32[/latex], so then we will subtract both sides by [latex]32[/latex].
The last step is to isolate the variable [latex]x[/latex] by itself on the left side of the equation. Since [latex]+5[/latex] is multiplying [latex]x[/latex], then its opposite operation is to divide by [latex]+5[/latex]. And so, let’s divide both sides by [latex]5[/latex] and we are done!
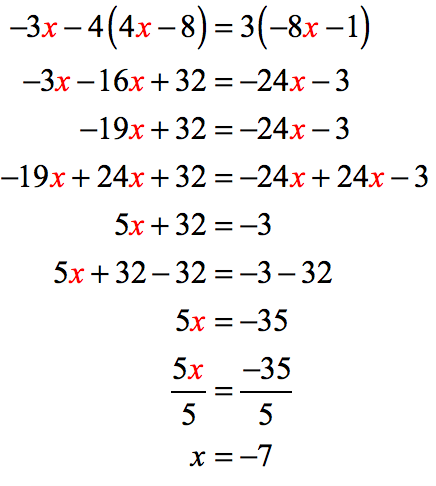
Example 4: Solve the equation [latex]13x – 9x + 20 = 30 + 2[/latex].
Step-by-Step Solution:
1) Combine the variables on the left side of the equation. That is, [latex]13x – 9x=4x[/latex]. Also, simplify the constants on the right side which gives us [latex]30+2=32[/latex].
2) Get rid of [latex]20[/latex] on the left side by subtracting [latex]20[/latex] on both sides of the equation.
3) To solve for [latex]x[/latex], divide both sides by [latex]4[/latex] to get [latex]x=3[/latex].
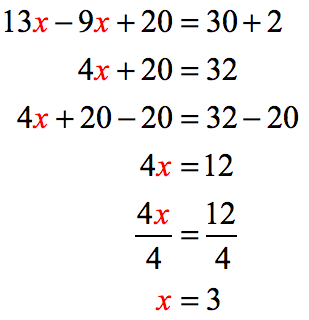
Example 5: Solve the equation below.
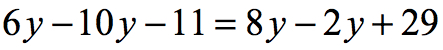
Step-by-Step Solution:
1) Combine like terms on both sides.
2) Subtract [latex]6y[/latex] on both sides to keep the variable [latex]y[/latex] to the left side only.
3) Add [latex]11[/latex] to both sides of the equation.
4) Finally, divide both sides by [latex]-10[/latex] to get the solution.
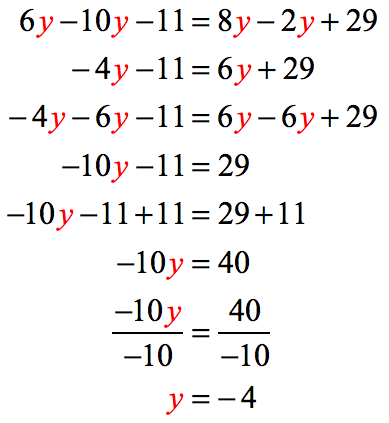
Example 6: Solve the equation below.
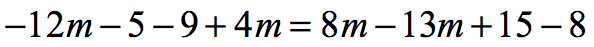
Step-by-Step Solution:
1) Combine the similar terms with variable [latex]m[/latex], and constants on both sides of the equation.
2) Add [latex]5m[/latex] to both sides of the equation. It will keep the variable on the left side and eliminate the variable on the right.
3) Add [latex]14[/latex] to both sides.
4) The last step is to divide the one-step equation by [latex]-3[/latex] to get the value of [latex]m[/latex].
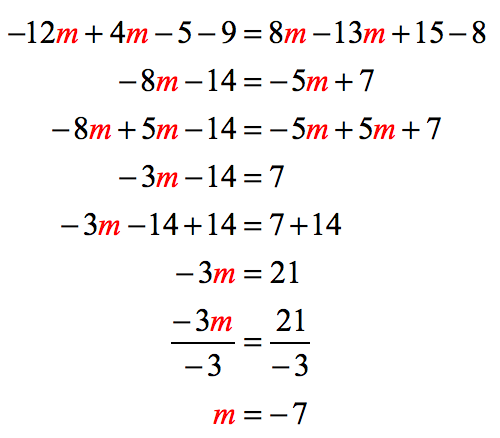
Example 7: Solve the equation [latex]2\left( {x – 5} \right) = 5x + 23[/latex].
Step-by-Step Solution:
1) Eliminate the parenthesis on the left side of the equation by distributing the number outside the parenthesis into the binomial inside.
2) This time, for convenience, we will keep the variable to the right side. To do that, we subtract [latex]2x[/latex] on both sides of the equation.
3) Next, subtract [latex]23[/latex] to both sides of the equation.
4) This leaves to simply divide both sides by the coefficient of [latex]3x[/latex] which is [latex]3[/latex] to get the value of [latex]x[/latex].
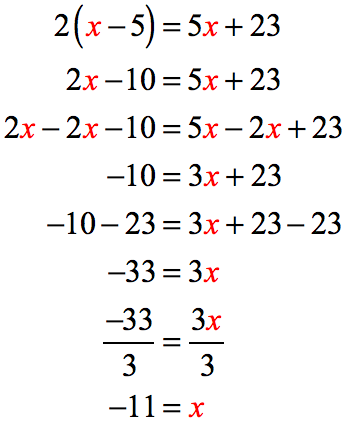
Example 8: Solve the equation below.
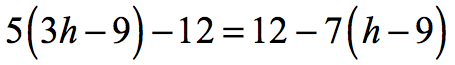
Step-by-Step Solution:
1) Remove the two parentheses on both sides of the linear equation by applying the Distributive Property of Multiplication over Addition.
2) Combine the constants on both sides. This will clean up the equation tremendously.
3) Add [latex]7h[/latex] to both sides to keep the term with a variable on the left while eliminating the one on the right.
4) Add [latex]57[/latex] on both sides of the equation to keep the constant on the right.
5) Divide both sides by [latex]22[/latex] to get the final solution. That’s it!
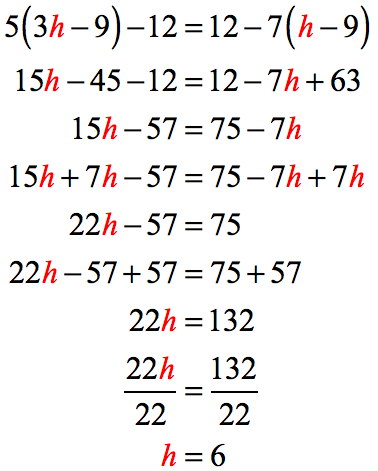
You may also be interested in these related math lessons or tutorials:
