Solving Two-Step Equations
There is no doubt that solving a two-step equation is extremely easy. As the name implies, two-step equations can be solved in just two steps. If this is your first encounter with two-step equations, don’t worry because we will go over enough examples to make you familiar with the process.
When solving an equation in general, we always keep in mind the notion that whatever we do to one side of the equation should also be done to the other side to ensure that the equation remains balanced.
We know that we have completely solved a two-step equation if the variable, usually represented by a letter in an alphabet, is isolated on one side of the equation (either left or right) and the number is located on the opposite side.
The USUAL way of solving a two-step equation:
Note: This is the “usual” method because most of the two-step equations are solved this way. Notice that Step 2 can alternatively be replaced by Step 3 which are the same essentially.
1) First, add or subtract both sides of the linear equation by the same number.
2) Secondly, multiply or divide both sides of the linear equation by the same number.
3)* Instead of step #2, always multiply both sides of the equation by the reciprocal of the coefficient of the variable.
Examples of How to Solve Two-Step Equations
Example 1: Solve the two-step equation below.
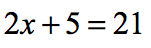
As the name of this linear equation suggests, it requires two steps in order to solve for the unknown variable. Generally, the first step involves getting rid of the number “farthest” from the term with a variable being solved. Then, we eliminate the number “closest” to the variable. The number is either multiplying or dividing the variable. It is also called the coefficient of the term.
The variable here is [latex]x[/latex]. Our goal is to solve [latex]x[/latex] by isolating it on one side of the equation. Keeping the variable on the left or on the right doesn’t make any difference. It is up to you! In this problem, let’s keep it on the left side since it’s already there.
On the side (left side of the linear equation) where the variable is located, notice that [latex]2[/latex] is “closest” to variable [latex]x[/latex], and [latex]5[/latex] is “farthest” one.
This simple observation allows us to decide which number to eliminate first. It is obviously [latex]+5[/latex] because it is farther between the two. The opposite of [latex]+5[/latex] is [latex]-5[/latex], that means we will subtract both sides of the equation by [latex]5[/latex].
After eliminating [latex]5[/latex] on the left side of the equation by subtracting both sides by [latex]5[/latex], it’s time to get rid of the number closest or directly attached to [latex]x[/latex] which is [latex]2[/latex] in [latex]2x[/latex]. Since [latex]2[/latex] is multiplying the variable [latex]x[/latex], its opposite operation is to divide by [latex]2[/latex].
After dividing both sides by [latex]2[/latex], we obtain the final answer or solution to the given two-step linear equation.
Just a quick reminder, it is considered solved because the coefficient of the variable is just
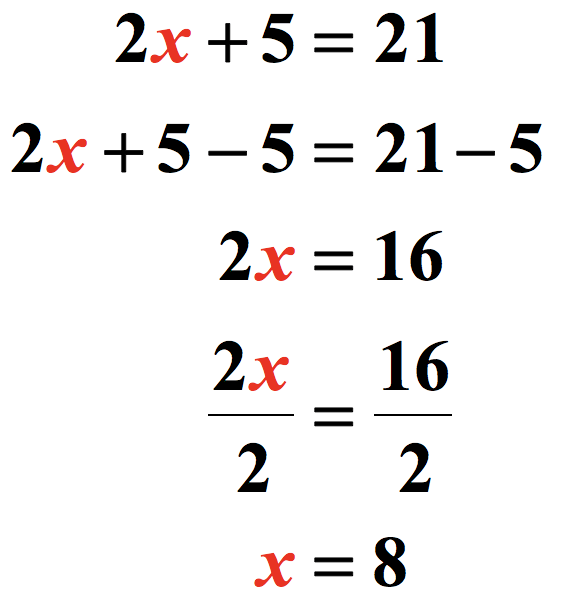
Example 2: Solve the two-step equation below.
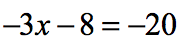
Our goal is to keep the variable [latex]x[/latex] on one side of the equation. It doesn’t matter which side, however it is a “standard” practice to keep the variable being solved to the left side. Some algebra teachers may require you to keep the variable to the left and there’s nothing with that. Personally, I don’t mind where you keep the variable, either left or right, as long as the isolated variable on one side of the equation has a coefficient of [latex]+1[/latex].
The first step involves removing the number “farthest” from variable [latex]x[/latex]. Notice that [latex]-3[/latex] is “closest” to [latex]x[/latex], while [latex]-8[/latex] is “farther away”. So then, we can eliminate [latex]-8[/latex] by adding to its opposite which is [latex]+8[/latex].
The second step involves getting rid of the number closest to the variable [latex]x[/latex] which is [latex]-3[/latex]. Since [latex]-3[/latex] is multiplying the variable x, its opposite operation is to divide by [latex]-3[/latex]. After dividing both sides by [latex]-3[/latex], we have solved the linear equation.
Quick reminder, [latex]-3[/latex] divided by [latex]-3[/latex] is equal to [latex]+1[/latex].
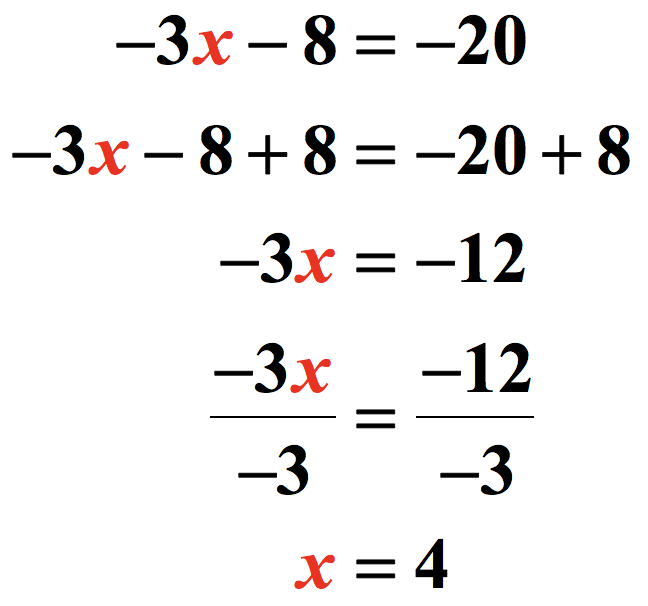
Example 3: Solve the two-step equation below.
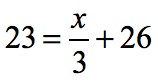
Here’s a situation where we can isolate the variable [latex]x[/latex] to the right side of the equation since it is already there.
Looking at the right side of the equation where the variable is located, the number [latex]3[/latex] is closest to [latex]x[/latex] because [latex]3[/latex] is dividing the variable [latex]x[/latex]. On the other hand, the number [latex]26[/latex] is “farther away”. This implies that we will have to deal with [latex]+26[/latex] by subtracting both sides of the equation by [latex]26[/latex]. The reason we subtract is that the additive inverse of [latex]+26[/latex] is [latex]-26[/latex].
The second step is to get rid of the denominator [latex]3[/latex]. Since [latex]3[/latex] is dividing the [latex]x[/latex], its opposite operation is to multiply by [latex]3[/latex].
After multiplying both sides by [latex]3[/latex], we have arrived at the final answer. You may rewrite your final answer as [latex]x = -9[/latex].
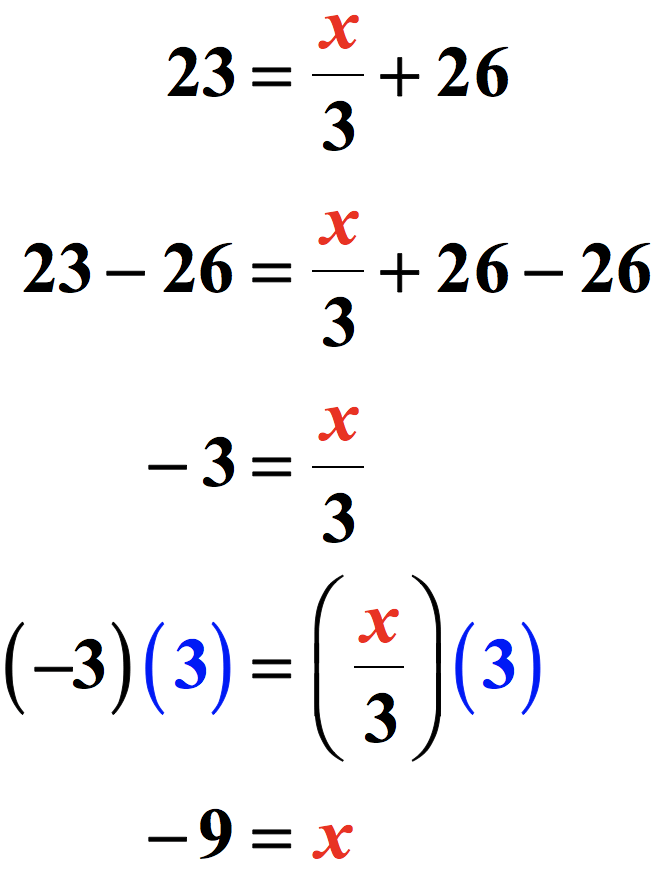
Example 4: Solve the two-equation below.
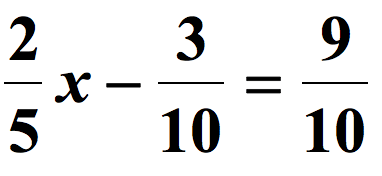
This may appear to be a multi-step equation, but it is not. It can be solved in two steps. Don’t be bothered by the fractions because they are very easy to deal with. In this case, you will apply the rule of fraction addition. The rule states that if you are adding two fractions that have the same denominator, just add the numerators then copy the common denominator.
Back to solving the two-step equation above, to remove the fraction on the left side which is [latex]\Large{ – {3 \over {10}}}[/latex], we will add [latex]\Large{{3 \over {10}}}[/latex] to both sides of the equation.
The reason that we are adding instead of subtracting is
After adding [latex]\Large{{3 \over {10}}}[/latex] to both sides, only [latex]{\Large{{2 \over 5}}}x[/latex] remains on the left side.
For the right side of the equation, we have [latex]\Large{{9 \over {10}} + {3 \over {10}} = {{12} \over {10}}}[/latex].
Everything I stated above is just the first step. Now, moving on to the second step. Look at the coefficient of the variable [latex]x[/latex]. It is [latex]\Large{{2 \over 5}}[/latex] that means its reciprocal is [latex]\Large{{5 \over 2}}[/latex].
To finally solve the given equation, we will multiply both sides of the equation by the reciprocal of the coefficient of the variable in question. Here’s the complete step-by-step solution:
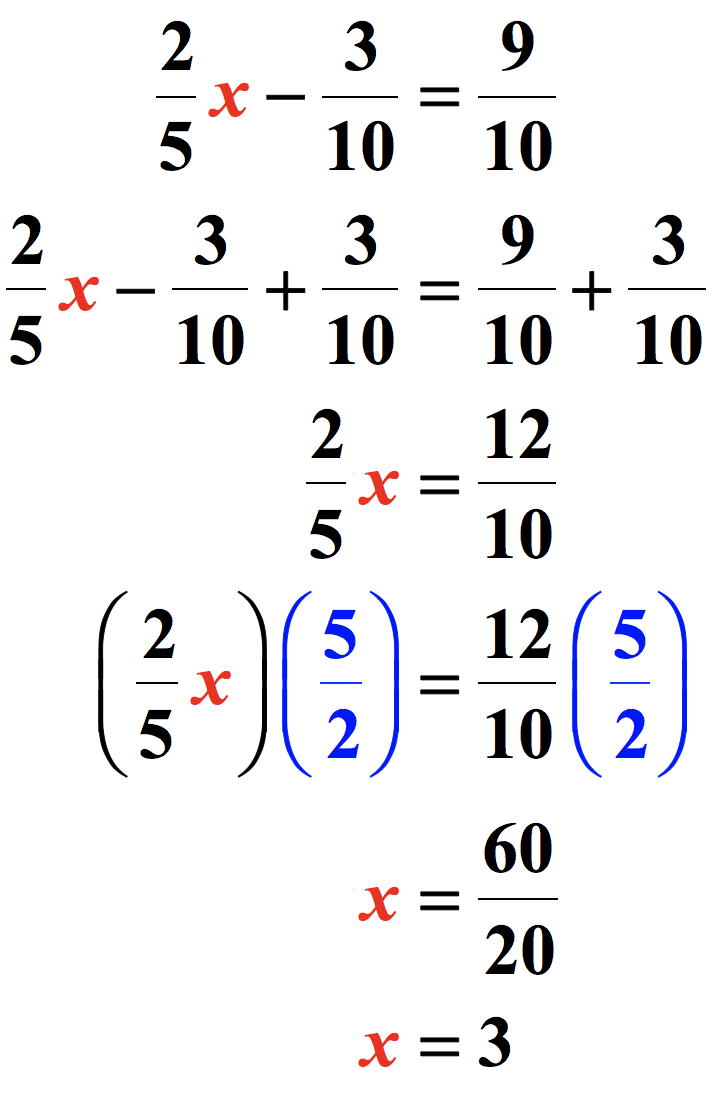
You may also be interested in these related math lessons or tutorials:
