Multi-Step Equations Practice Problems with Answers
For this exercise, I have prepared seven (7) multi-step equations for you to practice. If you feel the need to review the techniques involved in solving multi-step equations, take a short detour to review my other lesson about it. Click the link below to take you there!
1) Solve the multi-step equation for [latex]\large{c}[/latex].
[latex]c – 20 = 4 – 3c[/latex]
Answer
Add both sides by [latex]20[/latex]. Next, add [latex]3c[/latex] to both sides. Finally, divide both sides by the coefficient of [latex]4c[/latex] which is [latex]4[/latex] to get [latex]c=6[/latex].
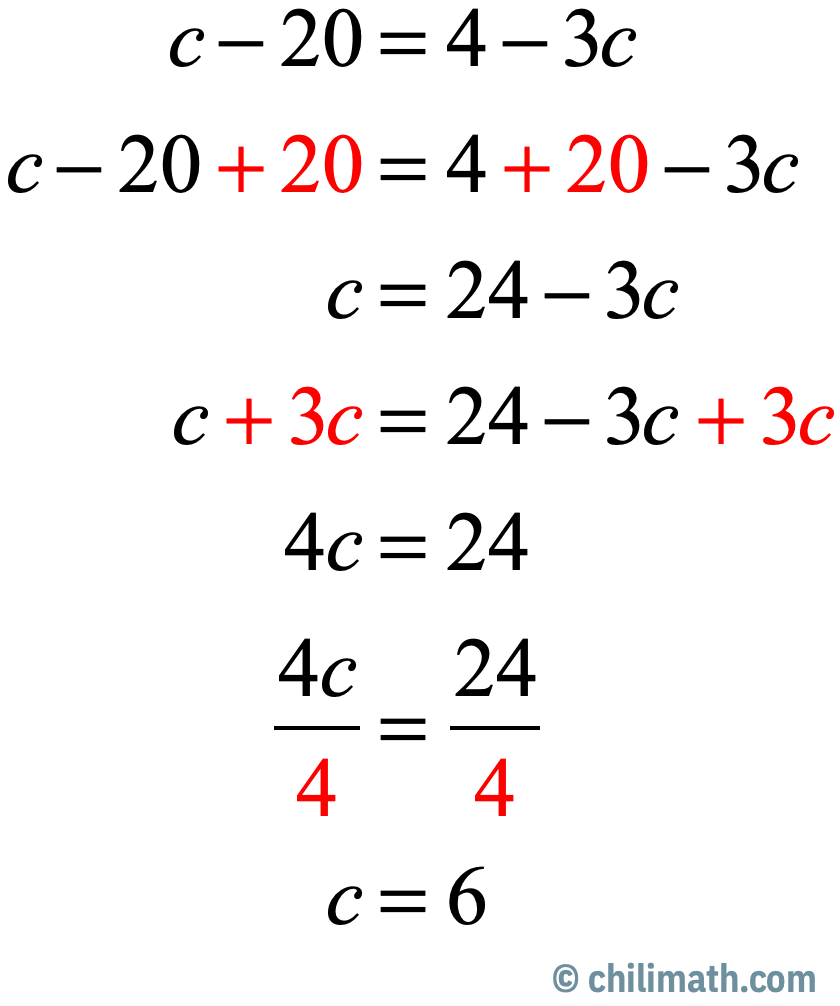
2) Solve the multi-step equation for [latex]\large{n}[/latex].
[latex] – \,4\left( { – 3n – 8} \right) = 10n + 20[/latex]
Answer
- Remember to always perform the same operation on both sides of the equation.
- Subtract by [latex]32[/latex].
- Subtract by [latex]10n[/latex].
- Divide by [latex]2[/latex]
- The final solution is [latex]n=-6[/latex].
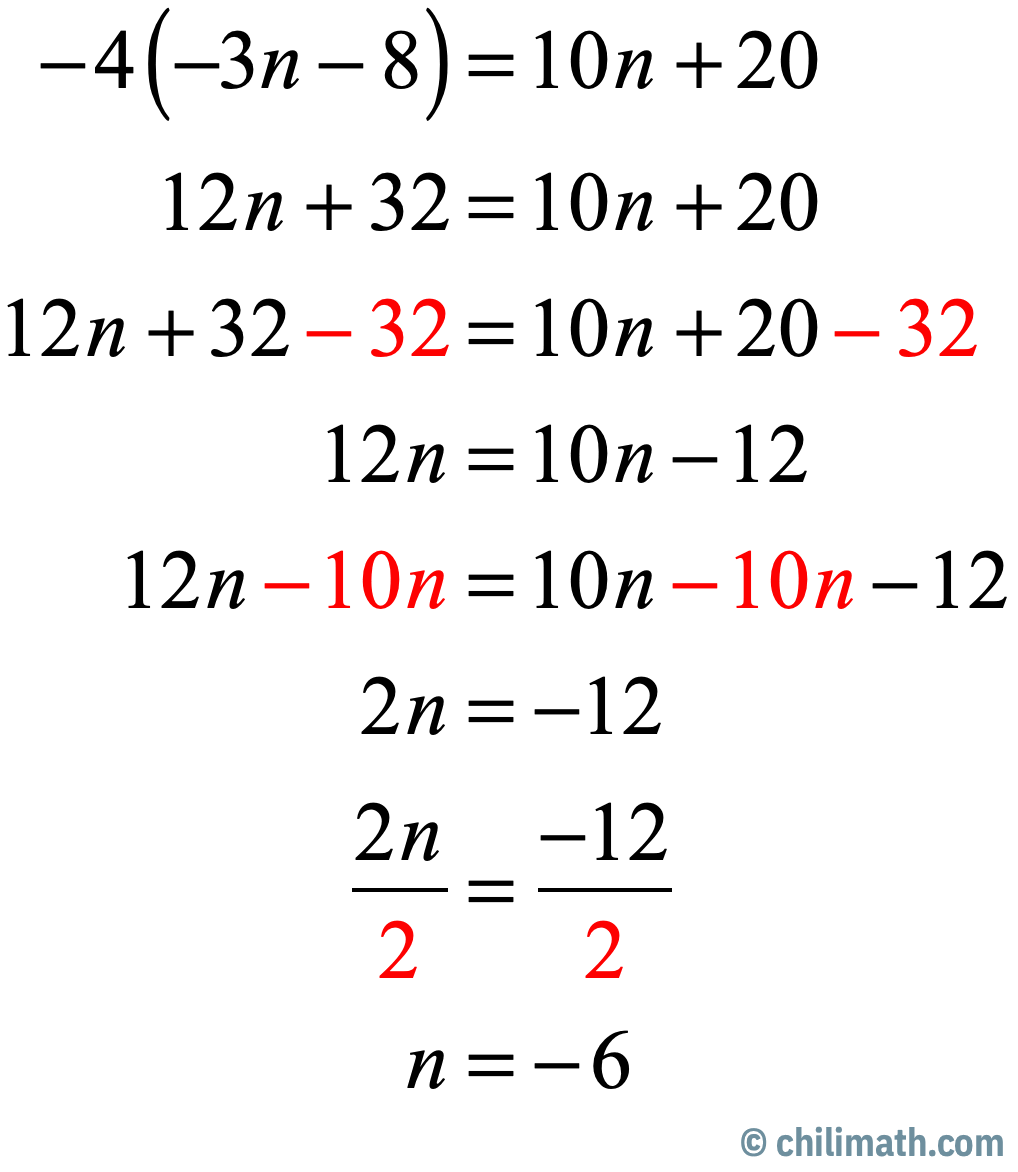
3) Solve the multi-step equation for [latex]\large{y}[/latex].
[latex]2\left( {4 – y} \right) – 3\left( {y + 3} \right) = – 11[/latex]
Answer
Apply twice the Distributive Property of Multiplication over Addition to the left side of the equation. Then combine like terms. Add both sides by [latex]1[/latex] followed by dividing both sides of the equation by [latex]-5[/latex].
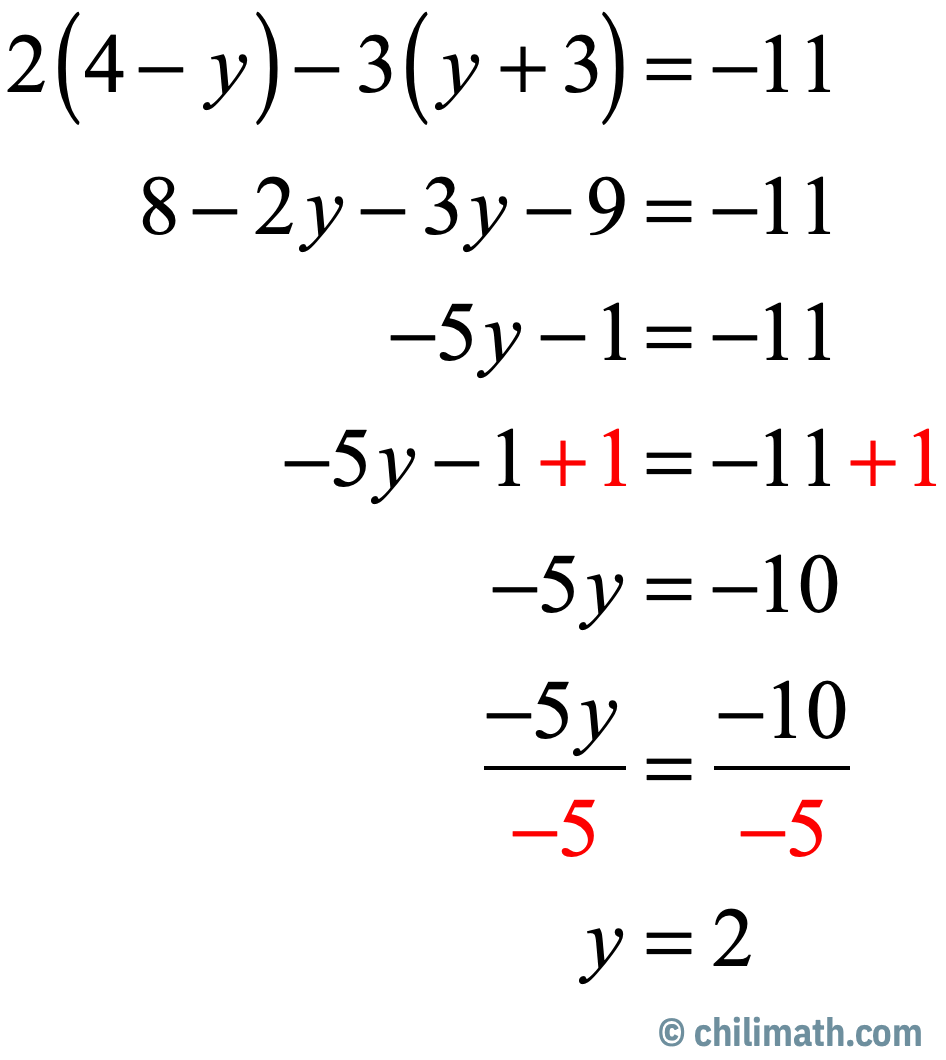
4) Solve the multi-step equation for [latex]\large{k}[/latex].
[latex]{\Large{{6k + 4} \over 2}} = 2k – 11[/latex]
Answer
Multiply both sides by [latex]2[/latex]. Next, subtract [latex]4[/latex] to both sides. Then, subtract [latex]4k[/latex]. Finally, divide by [latex]2[/latex] to obtain the value of [latex]k[/latex] which is [latex]-13[/latex].
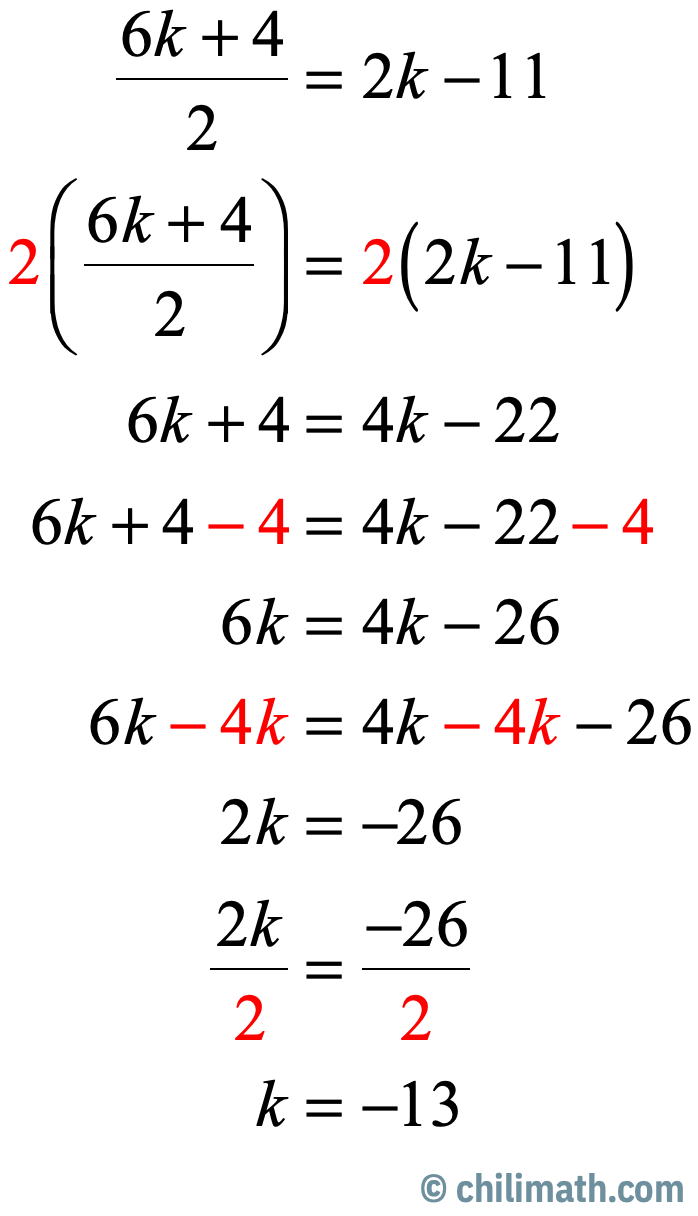
5) Solve the multi-step equation for [latex]\large{x}[/latex].
[latex] – \left( { – 8 – 3x} \right) = – 2\left( {1 – x} \right) + 6x[/latex]
Answer
Apply the Distributive Property on both sides of the equation. Be careful when multiplying expressions with the same or different signs. Next, add [latex]2[/latex] to both sides, then subtract [latex]3x[/latex], and finally finish it off by dividing [latex]5[/latex] to both sides.
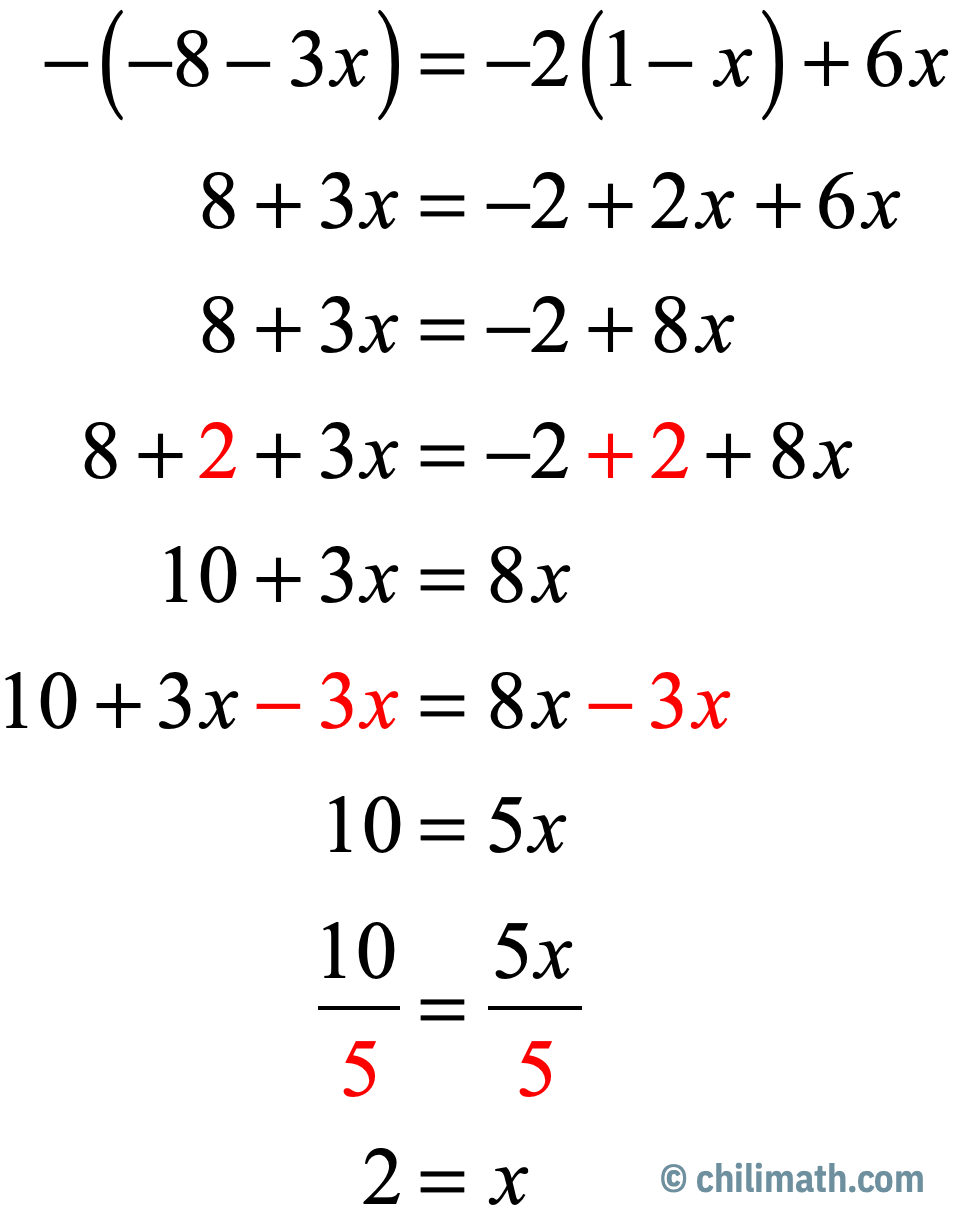
6) Solve the multi-step equation for [latex]\large{m}[/latex].
[latex]{\large{3 \over 4}}m – 2\left( {m – 1} \right) = {\large{1 \over 4}}m + 5[/latex]
Answer
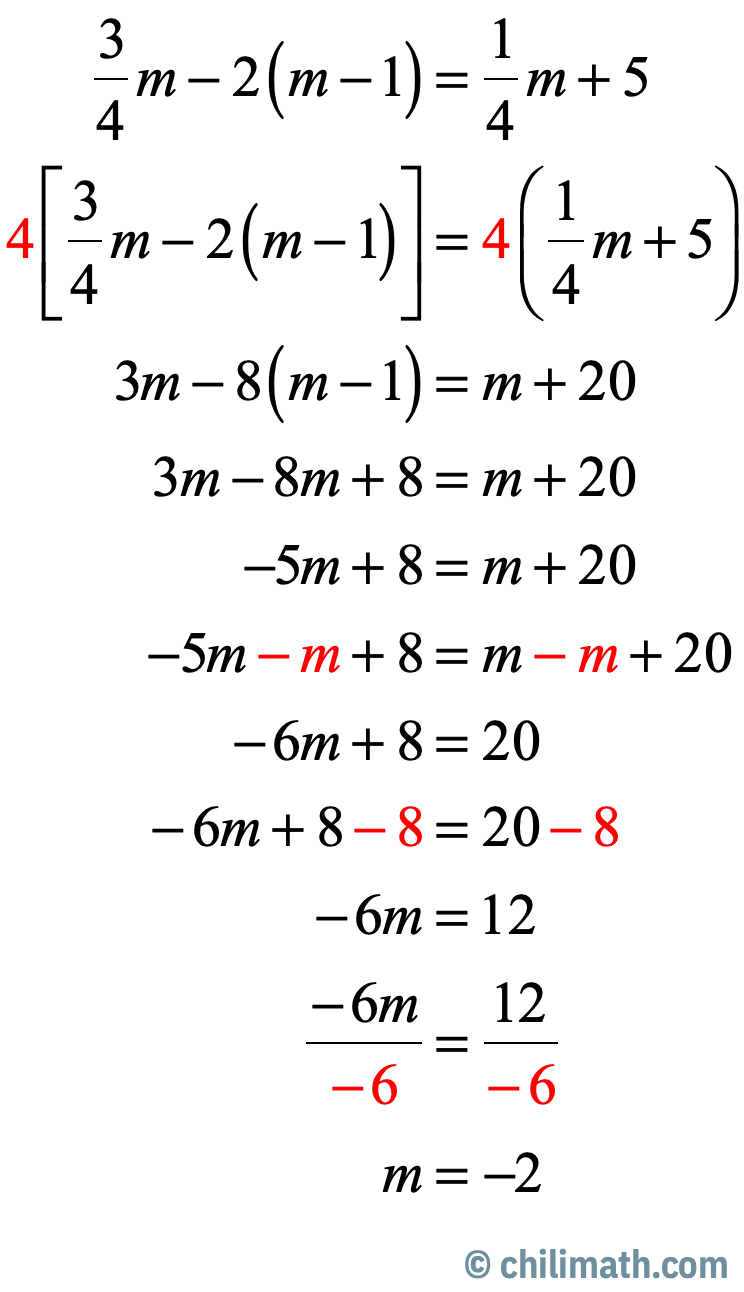
7) Solve the multi-step equation for [latex]\large{x}[/latex].
[latex]3\left( {3x – 8} \right) – 5\left( {3x – 8} \right) = 4\left( {x – 2} \right) – 6\left( {x – 2} \right)[/latex]
Answer
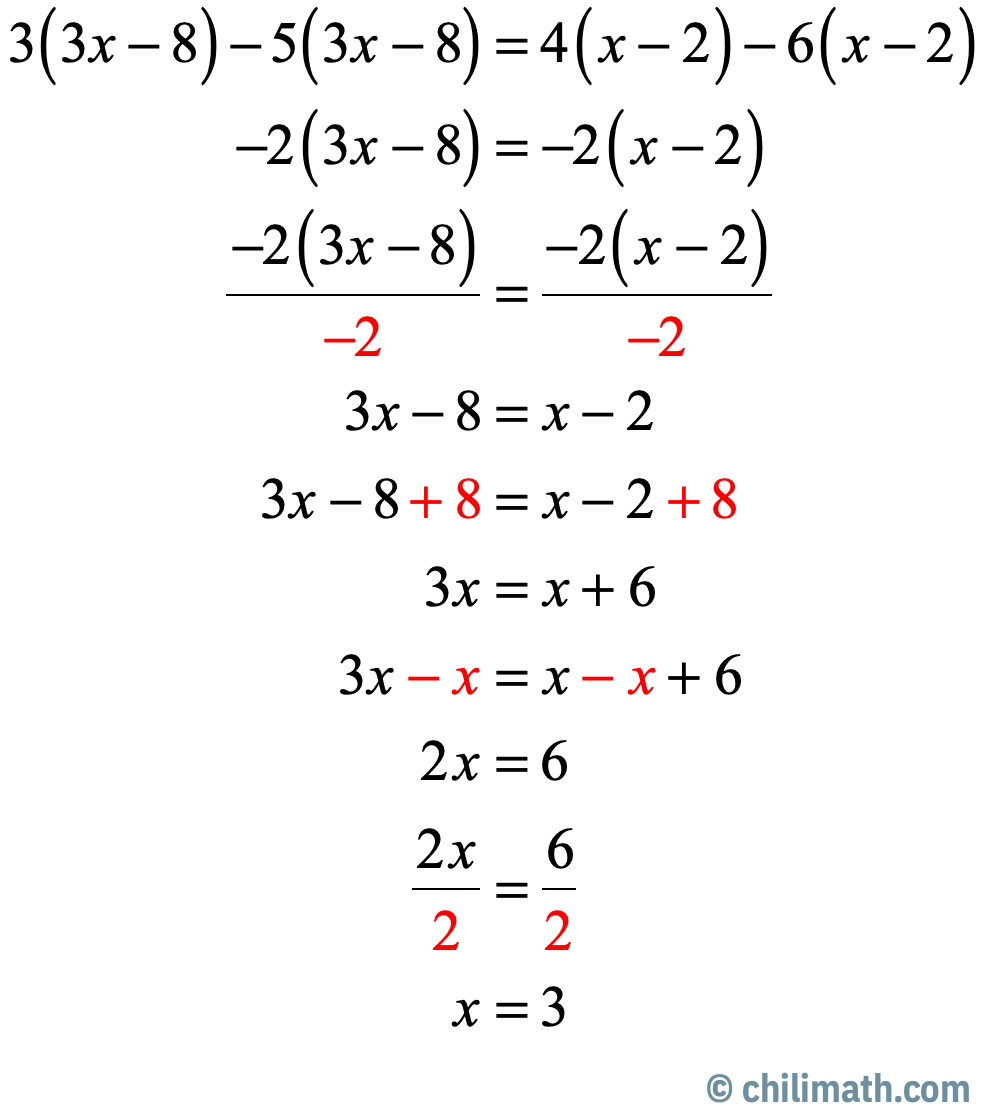
You may also be interested in these related math lessons or tutorials:

