Solving One-Step Equations
Solving one-step equations is truly your “first step” in the world of solving linear equations. If you can solve one-step equations, you are prepared to handle the challenge of more complex equations such as two-step and multi-step equations. Believe me, it is not difficult. Once you’ve mastered this particular skill, you open yourself up to many possibilities.
In this lesson, we are going to cover five (5) types or cases of one-step equations based on how they are solved. However, the fifth type is really the mixture or combination of the multiplication and division performed as one operation. This is really an important case because others may consider it a two-step equation problem when in fact, it can be solved with a single step.
Five (5) Cases of Solving One-Step Equations
- Case 1: Equations that are solvable by adding the same number to both sides of the equation.
- Case 2: Equations that are solvable by subtracting the same number to both sides of the equation.
- Case 3: Equations that are solvable by multiplying the same number to both sides of the equation.
- Case 4: Equations that are solvable by dividing the same number to both sides of the equation.
- Case 5: Equations that are solvable by multiplying the reciprocal of the coefficient of the term with a variable to both sides of the equation.
What does it mean to solve an equation?
Here’s a simple answer. If you can isolate or keep the variable by itself on one side of the equation (the left side or right side) such that the variable or letter has a coefficient of +1 while the constant or number is on the opposite side, then you have just solved the equation in question.
Examples of How to Solve One-Step Equations
Example 1: Solve the one-step equation.

Observe that the left side of the equation contains the variable x which is being subtracted by [latex]3[/latex] while the right side contains the number positive nine, [latex]+9[/latex]. Since the variable is already on the left side, let’s just keep it there.
However, to isolate the variable [latex]x[/latex], we have to get rid of [latex]-3[/latex]. We can eliminate [latex]-3[/latex] by adding its opposite which is [latex]+3[/latex]. To keep the equation balanced, we must also add [latex]+3[/latex] on the right side of the equation.
To reiterate, this is Case 1 of solving one-step equations because we added the same number to both sides of the equation.
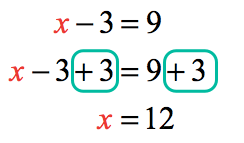
Example 2: Solve the one-step equation.
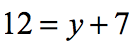
This one-step linear equation is a bit different as compared to the first example. Notice that the variable is located on the right side of the equation. Don’t be bothered by it because it is not a big deal.
Remember that when solving an equation, you may keep the variable on either side of the equation. As long as in the end, the variable that you are solving is isolated on one side with a coefficient of [latex]+1[/latex]. Therefore for this equation, it is convenient to keep the variable on the right side.
It is easy to see that subtracting both sides of the equation by [latex]7[/latex] will do the “trick” because it will get rid of the [latex]+7[/latex] thereby isolating the variable [latex]y[/latex] on the right side.
This is Case 2 since we subtracted the equation on both sides by the same number to solve it.

Example 3: Solve the one-step equation.
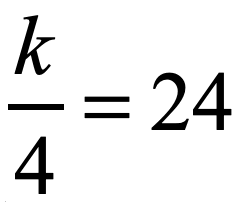
In this problem, our variable “[latex]k[/latex]” is divided by [latex]4[/latex]. Remember that our goal is to always isolate the variable on one side of the equation. Therefore, we have to find an operation that can undo division.
The operation that can undo division is multiplication. That means we will multiply both sides of the equation by [latex]4[/latex].
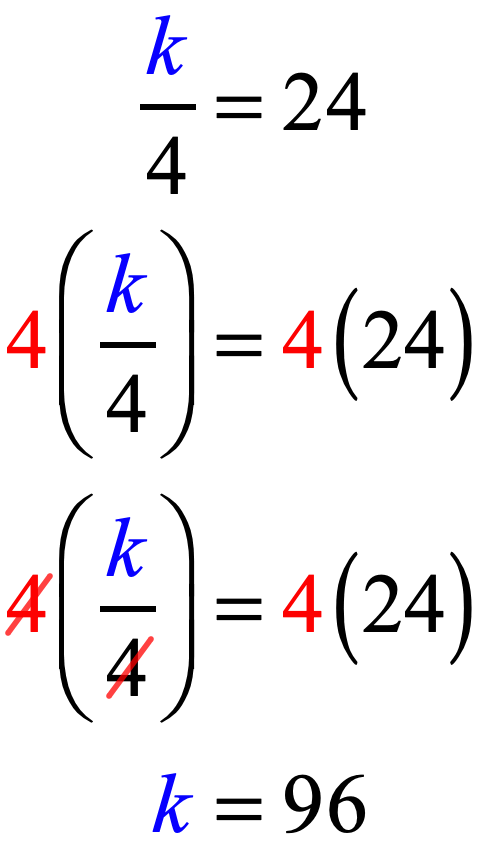
Example 4: Solve the one-step equation.
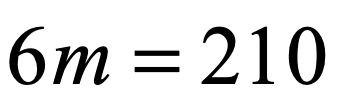
In example #3, a variable is being divided by a number. This time, we have a variable being multiplied by a number. To get rid of the number [latex]6[/latex] that is multiplying the variable [latex]m[/latex], we are going to divide both sides by [latex]6[/latex]. We use division to undo or cancel the effect of multiplication.

Example 5: Solve the one-step equation.

Many students are thrown off with this type of one-step equation because of the presence of a fraction as the coefficient. That is, [latex]\Large{5 \over 7}[/latex] in this case.
So how do we eliminate the fraction [latex]\Large{5 \over 7}[/latex]? When we say that we want to eliminate the fraction, it doesn’t mean that we must make it zero. Instead, we mean to convert it into [latex]\large\color{red}1[/latex].
The only way to do it is to multiply the fraction by its reciprocal.
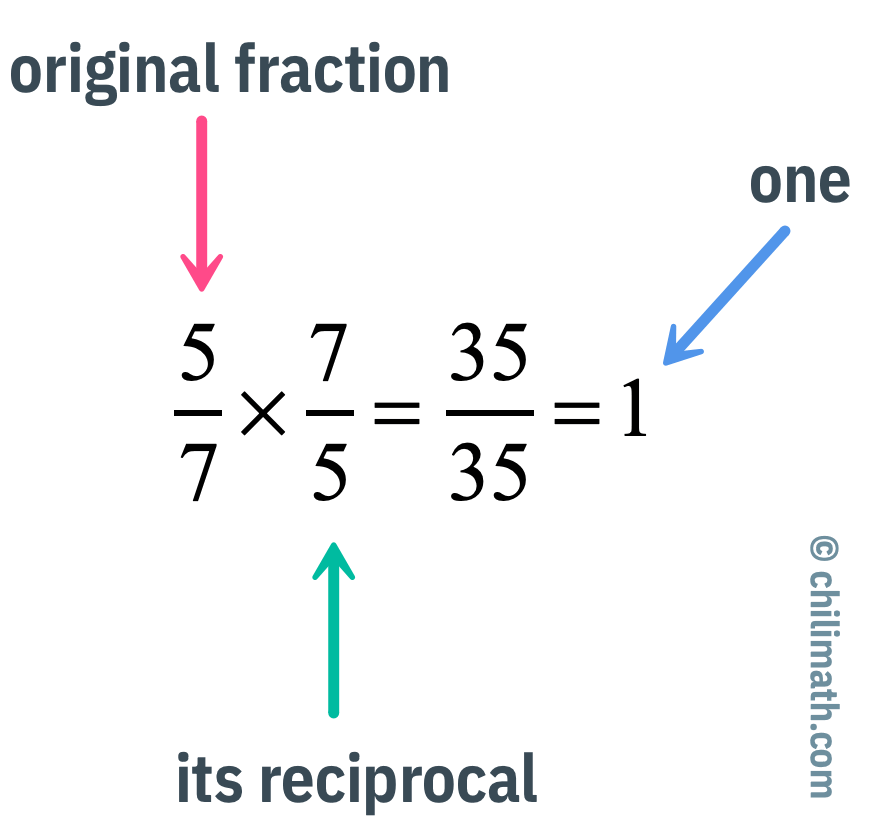
Therefore, to solve this equation we will multiply both sides by [latex]\Large{7 \over 5}[/latex] which is the reciprocal of the coefficient.
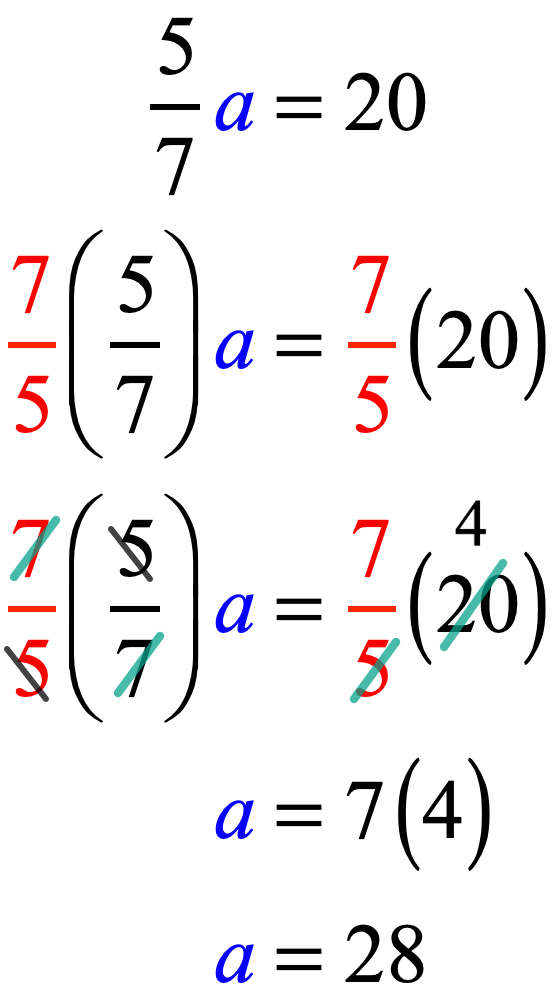
You may also be interested in these related math lessons or tutorials:
