Solving Literal Equations

Literal equations, simply put, are equations containing two or more variables. Your goal is to solve for just one variable with respect to others. If you know how to solve regular equations, then I guarantee you that solving literal equations will be a breeze.

What is a Literal Equation?

A literal equation is an equation that involves more than one variable. More so, a variable or “literal” is a math symbol that represents an arbitrary value or number. The letters in the alphabet are usually used to represent variables such as [latex]a[/latex], [latex]b[/latex], [latex]c[/latex], [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex]. To solve a literal equation means to express one variable with respect to the other variables in the equation.

Key Strategy to Solve Literal Equations

The “heart” of solving a literal equation is to isolate or keep by itself a certain variable on one side of the equation (either left or right) and the rest on the opposite side.

If you know how to solve regular One-Step Equations, Two-Step Equations, and Multi-Step Equations, the process of solving literal equations is very similar.

Therefore, you should not be intimidated by literal equations because you may have already the skills to tackle them. It’s just a matter of practice and familiarization.

So, the key idea looks like this. Notice that the variable that you want to solve is isolated on one side of the equation. In this case, it is on the left side. Observe that the variable [latex]\color{red}\Large{x}[/latex] is by itself on one side of the equation while the rest are on the opposite side.

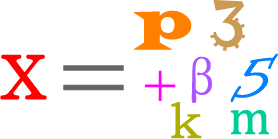
the solution of a literal equation may contain variables not just constants.

Let’s go over some examples!

An Example of One-Step Literal Equation

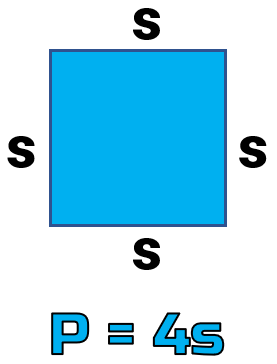
Example 1: Solve for [latex]s[/latex] in the literal equation [latex]P = 4s[/latex].

Remember this formula? This is the perimeter of a square where [latex]P[/latex] stands for perimeter and [latex]s[/latex] stands for the measure of one side of a square. Thus, to get the perimeter of a square we have [latex]P = s + s + s + s = 4s[/latex].

a blue square with a side measure of "s" which implies that its perimeter is four times the length of one side.

To solve for [latex]s[/latex], we need to get rid of the coefficient [latex]4[/latex] which is multiplying [latex]s[/latex]. The inverse of multiplication is division so that’s why we should divide both sides by [latex]4[/latex]!

We can isolate variable [latex]s[/latex] on the right side.

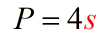
P is equal to the product of 4 and s. In short, we have P=4s.

Divide both sides by [latex]4[/latex].

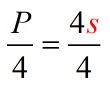
the quotient of P and 4 is equal to the quotient of 4s and 4. We can write this as P/4=(4s)/4.

Simplify. Now that the variable [latex]\color{red}\Large{s}[/latex] is alone on the right side of the equation, we are done!

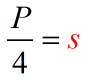
P divided by 4 equals s. We write this in an equation as P/4=s.

Examples of Two-Step Literal Equations

Example 2: Solve for [latex]L[/latex] in the literal equation [latex]P = 2L + 2W[/latex].

The literal equation mentioned above is also the formula to get the perimeter of a rectangle, where: [latex]P[/latex] = perimeter, [latex]L[/latex] = length, and [latex]W[/latex] = width. It is possible to isolate the variable [latex]L[/latex] on the right side. However, why not flip the equation around so we can keep the variable [latex]L[/latex] alone on the left? Well, sounds like a plan!

Don’t be intimidated by how it looks. Just focus on the things you want to do, that is to solve for [latex]L[/latex] and the rest of the steps will follow.

We want [latex]L[/latex] solved, right?

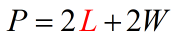
Flip around the equation to isolate the variable on the left side.

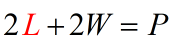
Subtract both sides by [latex]2W[/latex].

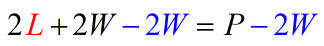
Simplify.

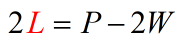
Divide both sides by [latex]2[/latex].

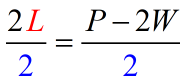
Simplify, now [latex]L[/latex] stands alone – solved!

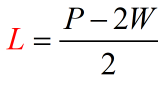
Example 3: Solve for [latex]x[/latex] in the literal equation below.

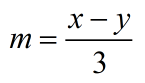
m is equal to the ratio of the difference of x and y, and 3. we can write this as m=(x-y)/3.

What makes this literal equation interesting is that we are going to isolate a variable that is part of the numerator of a fraction. I’m not sure if you remember that whenever you see something like this, try to get rid of the denominator first. This makes the entire solving process a lot simpler.

Since that denominator [latex]3[/latex] is dividing the expression “[latex]x − y[/latex]”, the opposite operation that can undo it is multiplication. It makes sense to multiply both sides by [latex]3[/latex] first, then add by “[latex]y[/latex]” to keep the [latex]x[/latex] by itself. Not too bad, right?

Okay, we want to solve for [latex]x[/latex]. Let’s isolate it on the right side.

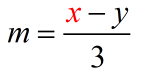
Start by multiplying both sides by [latex]3[/latex] which is the denominator of the fraction.

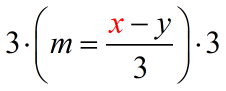
multiply 3 on both sides of the equation m=(x-y)/3.

Simplify. That’s good, the denominator is now gone.

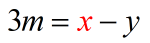
Add both sides by [latex]y[/latex]. That’s the only way to eliminate the [latex]− y[/latex] on the right side.

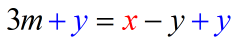
Simplify, [latex]x[/latex] is now happily by itself. Done!

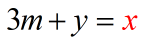
Examples of Multi-Step Literal Equations

Example 4: Solve for [latex]C[/latex] in the literal equation below.

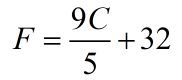
this is the formula to convert Celsius to Fahrenheit

This is the formula used to convert the measure of temperature in the Celsius unit to the Fahrenheit scale. Notice that to find the value of [latex]F[/latex] (Fahrenheit), we need to plug in some value of [latex]C[/latex] (Celsius).

However, can we also use the given formula to find Celsius whenever the value for Fahrenheit is given?

Absolutely yes!

This is a literal equation after all so it is possible to express [latex]C[/latex] in terms of [latex]F[/latex]. That’s what we’re going to do now…

All eyes are on [latex]C[/latex]. The goal is to isolate it.

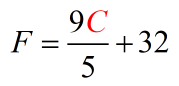
We’ll get rid of [latex]32[/latex] on the right by subtracting both sides by [latex]32[/latex].

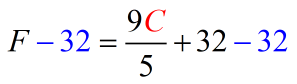
This looks cleaner after simplification.

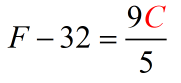
Next, multiply both sides by [latex]5[/latex] to cancel out the denominator [latex]5[/latex] under [latex]9C[/latex].

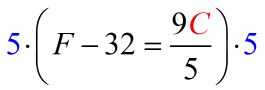
multiply 5 to both sides of the equation F-32=(9C)/5.

We’re getting there! I suggest not to distribute the [latex]5[/latex] into [latex](F − 32)[/latex].

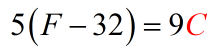
One more step, divide both sides by [latex]9[/latex] to finally isolate the variable on the right.

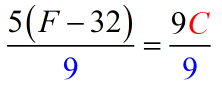
divide both sides by 9 to get the formula to determine Celsius value when a Fahrenheit temperature is given

That’s it! We have solved for [latex]C[/latex].

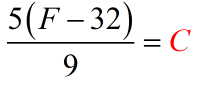
Example 5: Solve for [latex]h[/latex] in the literal equation [latex]3h + g = 5h − hg[/latex].

This is really interesting! Some of you might think that it is impossible to isolate the variable [latex]h[/latex] since it is found pretty much in three places: one [latex]h[/latex] on the left and two on the right. Well, don’t give up yet! Let me show you a little “secret”.

Use the factoring method to pick that variable [latex]h[/latex] out of the group. But before you could factor [latex]h[/latex] out, make sure that you move all the [latex]h[/latex]’s on one side of the equation.

Since we have two terms of [latex]h[/latex]’s on the right side, we might as well move the term [latex]3h[/latex] on the left to the other side.

We want [latex]h[/latex] isolated, right?

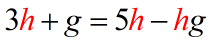
Keep all our [latex]h[/latex] terms on the right side. We can do that by subtracting both sides by [latex]3h[/latex].

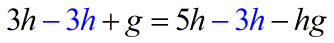
After simplification, it’s wonderful to see all our [latex]h[/latex] terms just on the right side.

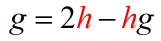
It’s obvious that the step should involve factoring [latex]h[/latex] out.

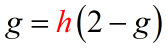
factor out h on the right side of the equation to get g=h(2-g).

Wow, this is great! Just a single [latex]h[/latex] on the right side.

To isolate [latex]h[/latex] by itself implies that we have to get rid of the expression [latex](2−g)[/latex].

Divide both sides by [latex](2 − g)[/latex].

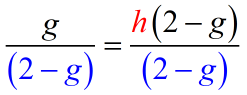
divide the entire literal equation by 2-g to isolate the variable h. g/(2-g)=/(2-g).

Do some cancellations on the right side.

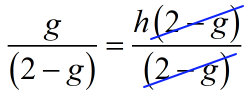
cancel out common terms which give us g/(2-g)=h(2-g)/(2-g).

That is it! We have solved for [latex]h[/latex].

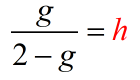
the final solution of the given literal equation is h=g/(2-g).

Example 6: Solve for [latex]x[/latex] in the literal equation below.

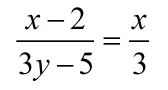
The most straightforward way of solving this literal equation is to perform cross multiplication. In doing so, the denominators on both sides of the equation should disappear.

From that point, we can apply the same strategy from Example 5 to solve for [latex]x[/latex] which involves gathering all [latex]x[/latex] terms on one side of the equation and then hopefully factoring the [latex]x[/latex] out.

In this equation, we have two [latex]x[/latex]’s on both sides of the equation. More importantly, they are located in the numerator position.

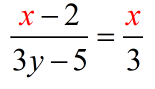
We want the denominators gone so without any hesitation we should apply the cross multiplication technique. Then simply apply the distributive property on both sides of the equation.

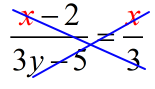
cross multiply (x-2) by 3 and (3y-5) by x

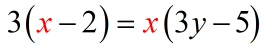
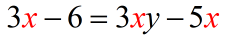
At this point, we decide where to keep or gather all our [latex]x[/latex]’s. For this example, let’s keep them on the left side.

Start by getting rid of the [latex]-5x[/latex] on the right by adding [latex]5x[/latex] on both sides.

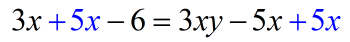
This is how it looks after simplification. The next step is to deal with the [latex]3xy[/latex] on the right side. We want to move it to the left as well.

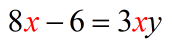
Subtract both sides by [latex]3xy[/latex]. That should keep all our [latex]x[/latex]’s on the left.

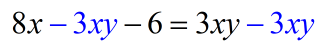
Don’t forget to write [latex]0[/latex] on the right side!

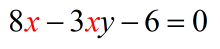
Now, the [latex]−6[/latex] on the left must be moved to the right side. We can do this by adding [latex]6[/latex] to both sides.

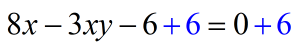
This is getting nicer! We have all our [latex]x[/latex] terms on the left. It appears that we can factor the [latex]x[/latex] out.

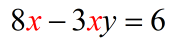
Yep! We just did!

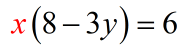
Finally, to solve [latex]x[/latex], we should divide both sides by the expression [latex](8 − 3y)[/latex]. Perform some cancellations.

And we’re done!

Take a Quiz!

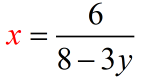
Literal Equations Quiz

You might be interested in:

Solving One-Step Equations

Solving Two-Step Equations

Solving Multi-Step Equations