Equations of Parallel and Perpendicular Lines
In this tutorial, you will learn how to construct a line that is either parallel or perpendicular to a given reference line and passing through a fixed point.
To be successful in solving this kind of problem, you need to have some background knowledge about the line itself.
First: You should know how to find the slope of a line given two points.
Here is the formula:
Slope Formula
The slope, [latex]m[/latex], of a line passing through two arbitrary points [latex]\left( {{x_1},{y_1}} \right)[/latex] and [latex]\left( {{x_2},{y_2}} \right)[/latex] is calculated as follows…
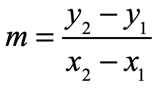
Second: Be familiar with the two (2) most useful forms of the line, namely: Slope Intercept Form and Point Slope Form.
Slope-Intercept Form
The linear equation written in the form [latex]y = mx + b[/latex] is in slope-intercept form where:
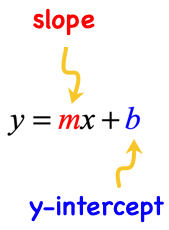
Point-Slope Form
The equation of the line with a slope, [latex]m[/latex], and passing through a specific point [latex]{x_1} – {y_1}[/latex] is
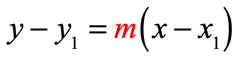
Third: You need to know the basic facts about parallelism and perpendicularity of lines using their slopes.
Assume that you have two distinct and nonvertical lines, [latex]{\ell _1}[/latex] and [latex]{\ell _2}[/latex] in Slope-Intercept Form.
- Line 1:
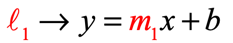
- Line 2:
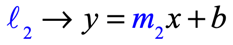
They are parallel lines if their slopes are equal or the same.
- Equal Slopes:
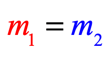
- Graph:
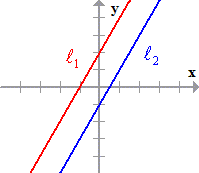
Definition of Parallel Lines
Note: Two lines on the same plane are parallel if they have the same distance and will never meet or will never intersect.
They are perpendicular lines if their slopes are opposite reciprocals of each other, or the product of their slopes equals [latex] – 1[/latex].
- Slopes are Opposite Reciprocals:
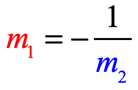
- Product of Slopes:

- Graph:
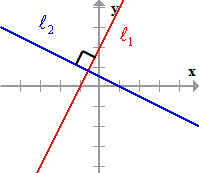
Definition of Perpendicular Lines
Note: Two lines on the same plane are perpendicular if they intersect or meet at a [latex]90^\circ[/latex] degree angle.
Let’s go over some examples!
Examples of How to Find the Equation of a Line Parallel and/or Perpendicular to Another Line
Example 1: Find the equation of a line that is parallel to [latex]y = – \,3x + 5[/latex] and passing through the point [latex]\left( {2, – \,7} \right)[/latex].
Let’s start by graphing the given line and point so that we have a clear picture of what’s going on.
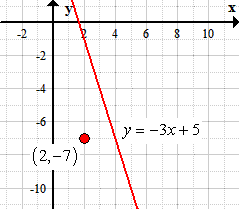
To construct the required line, we need two things: a slope and a point. Once we have this information, we can plug these values into the Point-Slope Form, and finally rewrite it in Slope-Intercept to get our final answer.
We can directly use the slope of the reference line [latex]y = – \,3x + 5[/latex], which is [latex]m = – \,3[/latex] because they must have equal slopes in order to be parallel. We will use [latex]\left( {2, – \,7} \right)[/latex] as the point where this unknown line must pass through.
Therefore, the line that we are trying to determine is the one with a slope of [latex]m = – \,3[/latex] and passing through [latex]\left( {2, – \,7} \right)[/latex].
Substitute these values into the Point-Slope Form and solve for “[latex]y = [/latex]“.
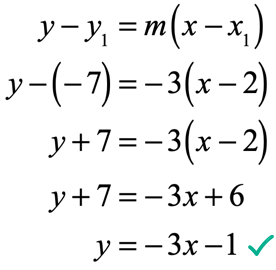
This is how it looks on the graph.
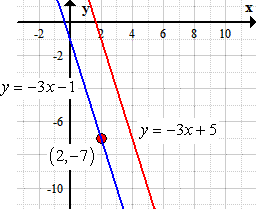
Example 2: Find the equation of a line that is perpendicular to [latex]y = {1 \over 5}x – 2[/latex] , and passing through the point [latex]\left( {1, – \,3} \right)[/latex].
This is the graph of the given line and the point.
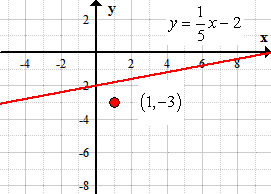
Can we use the slope [latex]m = {1 \over 5}[/latex] of the reference line in the calculation? The answer is no! Use this only as the slope of the parallel line because they must be equal. Instead, take the opposite reciprocal (also known as negative reciprocal) of the given slope [latex]m = {1 \over 5}[/latex] to get the needed perpendicular slope.
The opposite reciprocal of [latex]m = {1 \over 5}[/latex] is [latex]m = – \,5[/latex].
Therefore, to get the equation of the perpendicular line, use [latex]m = – \,5[/latex] and the point [latex]\left( {1, – \,3} \right)[/latex]. Plug these values in the
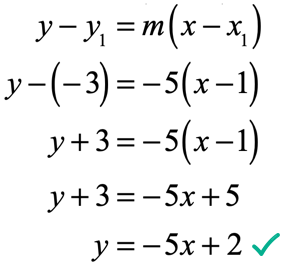
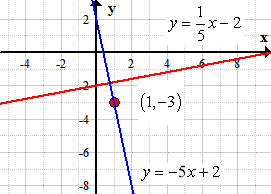
Graph the line to verify if it is perpendicular to the reference line and has passed through the fixed point, which is the case!
Example 3: Find the lines that are parallel and perpendicular to [latex]y = {2 \over 5}x + 7[/latex] and passing through the point [latex]\left( { – 1, – \,2} \right)[/latex].
In this problem, we are going to have two answers. One answer is the line that is parallel to the reference line and passing through a given point. Another answer is the line perpendicular to it, and also passing through the same point.
- Part 1: Determine the parallel line using the slope [latex]m = {2 \over 5}[/latex] and the point [latex]\left( { – 1, – \,2} \right)[/latex].
We will use the slope of the reference line because we want to find the line that is parallel to it, which means, they must have equal slopes. Substitute the values in the Point Slope Form and then transform into Slope Intercept Form as the final answer.
![y-ysub1 = m(x-xsub1) → y-(-2) = 2/5[x-(-1)] → y+2 = 2/5(x+1) → y=-(8/5).](https://www.chilimath.com/wp-content/uploads/2019/02/ppl-ex3a.png)
- Part 2: Determine the parallel line using the slope [latex]m = {{ – \,5} \over 2}[/latex] and the point [latex]\left( { – 1, – \,2} \right)[/latex].
The perpendicular slope will be the opposite reciprocal of the reference line’s slope. Thus, [latex]{2 \over 5} \to {{ – \,5} \over 2}[/latex] .
![y-ysub1 = m(x-xsub1) → y-(-2) = (-5)/2[x-(-1)] → y+2 = (x+1) → y=-(9/2)](https://www.chilimath.com/wp-content/uploads/2019/02/ppl-ex3b.png)
Example 4: Find the equation of a line that is parallel to [latex]y = {5 \over 2}x – 4[/latex], and passes through the point [latex]\left( { – \,2,\,\,1} \right)[/latex].
Solution:
Since we want a parallel line, the slope is taken straight out of the reference line, that is, [latex]m = {5 \over 2}[/latex]. And the point to use will be the one that is given to us which is [latex]\left( { – \,2,\,\,1} \right)[/latex]. Plug the values into the
![y-ysub1 = m(x-xsub1) → y-1 = 5/2[x-(-2)] → y = +6](https://www.chilimath.com/wp-content/uploads/2019/02/ppl-ex4a.png)
Example 5: Find the equation of a line that is perpendicular to [latex]y = {{ – 1} \over 2}x + 2[/latex], and passes through the point [latex]\left( { – 10, – \,5} \right)[/latex].
Solution:
The slope to use will be the opposite reciprocal of the slope of the reference line. The slope of the reference line is [latex]m = {{ – 1} \over 2}[/latex]. That means its opposite reciprocal will be [latex]m = 2[/latex].
Substitute the values for slope [latex]m = 2[/latex] and for the point [latex]\left( { – 10, – \,5} \right)[/latex] into the
![y-ysub1 = m(x-xsub1) → y-(-5) = 2[x-(-10)] → y = 2x+15](https://www.chilimath.com/wp-content/uploads/2019/02/ppl-ex5a.png)
Example 6: Find the lines that are parallel and perpendicular to [latex]y = {{ – \,3} \over 2}x – 15[/latex] and passes through the point [latex]\left( {0,2} \right)[/latex].
Solution:
To get the parallel line, use the slope [latex]m = {{ – \,3} \over 2}[/latex] and the point [latex]\left( {0,2} \right)[/latex]. Plug values into
![y-ysub1 = m(x-xsub1) → y-2 = (-3)/2[x-0] → y = (-3/2)x+2](https://www.chilimath.com/wp-content/uploads/2019/02/ppl-ex6a.png)
To get the perpendicular line, the slope to use will be the opposite reciprocal of the given slope [latex]m = {{ – \,3} \over 2}[/latex] which is [latex]m = {2 \over 3}[/latex] . And the point will simply be the given one, that is, [latex]\left( {0,2} \right)[/latex]. Plug values into
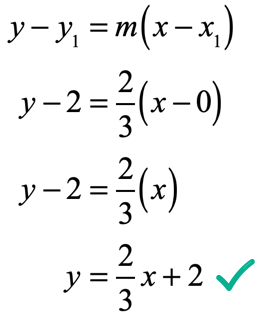
You may also be interested in these related math lessons or tutorials:
