Point-Slope Equation Form of a Line
Basically, the point-slope form is derived from the concept of finding the slope of a line when two points are given. In other words, if you can remember the slope formula then the point-slope form should naturally come to you.
Let’s start by reviewing the slope formula.
Slope Formula
The slope, [latex]m[/latex], of a line passing through two arbitrary points [latex]\left( {{x_1},{y_1}} \right)[/latex] and [latex]\left( {{x_2},{y_2}} \right)[/latex]is calculated as follows.
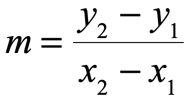
If we slightly tweak how the two points “look”, say for instance
- Let [latex]\left( {{x_1},{y_1}} \right)[/latex] be a specific point on a line
- Let [latex]\left( {x,y} \right)[/latex] be any other point on the line
Then we substitute those points into the slope formula, we get something like this
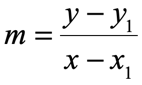
Multiply both sides of the equation by the denominator [latex]x – {x_1}[/latex]
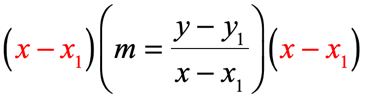
and cancel common factors.
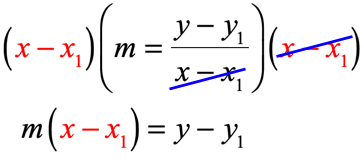
Finally, rewrite the equation such that the [latex]y[/latex]-variables are on the left side to get to the desired form.
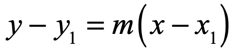
Yep! We have just derived the point-slope form of a line, using the slope formula as our starting point.
Let’s summarize the concept.
Point-Slope Form of a Line
The equation of the line with a slope, [latex]m[/latex], and passing through a specific point [latex]\left( {{x_1},{y_1}} \right)[/latex]is

Examples of Applying the Concept of Point-Slope Form of a Line
Example 1: Write the point-slope form of the line with a slope of [latex]3[/latex] which passes through the point [latex]\left( {2,5} \right)[/latex].
This is a standard textbook question that pretty much can be solved in seconds. However, let’s break down the process step by step in order for us to have a solid understanding of the procedure.
The slope is given as [latex]m = 3[/latex], and the point [latex]\left( {2,5} \right)[/latex] has coordinates of [latex]{x_1} = 2[/latex] and [latex]{y_1} = 5[/latex]. Now plug the known values into the slope-intercept form to get the final answer.
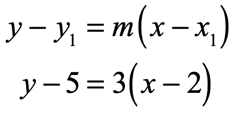
Example 2: Write the point-slope form of the line with a slope of [latex] – \,5[/latex] which passes through the point [latex]\left( { – \,1, – \,7} \right)[/latex].
This is very similar to example #1, but the reason for going over this is to emphasize what happens when the coordinates of the point have negative signs. We will have a case here where we are subtracting negative numbers. The result of that is having double negative signs which require us to make it positive. Remember the rule that two negative signs become positive. Right?
The given slope is just [latex]m = – \,5[/latex], and the point [latex]\left( { – \,1, – \,7} \right)[/latex] has coordinates of [latex]{x_1} = – \,1[/latex] and [latex]{y_1} = – \,7[/latex]. Substituting these known values into the slope-intercept formula, we get…
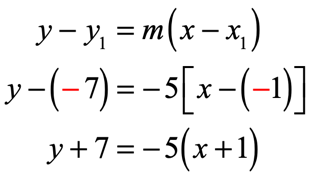
Example 3: Determine the point-slope form of the line passing through the points [latex]\left( {2,10} \right)[/latex] and [latex]\left( {5,1} \right)[/latex].
In order to write the equation of a line in point-slope form, we will need two essential things here which are the slope of the two given points and any point found on the line. Although the slope is not directly provided to us, we can absolutely solve for the slope using the Slope Formula because there are at least two points that we know of that are found on the line.
- Start by assigning the coordinates of the points.
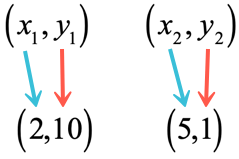
- Evaluate the values of the coordinates found above in the slope formula.
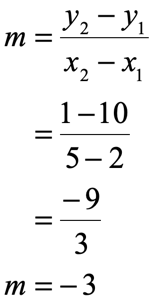
- The value of slope becomes [latex]m = – \,3[/latex].
The next step is to pick ANY of the two given points, [latex]\left( {2,10} \right)[/latex] or [latex]\left( {5,1} \right)[/latex]. Use the chosen point in conjunction with the slope [latex]m = – \,3[/latex] to write point-slope slope of the line.
Notice that it can actually be written in two ways because we have two points here. As an exercise, I will demonstrate that although the point-slope equations “look” different, they are actually equivalent or the same!
Tip: Solve both equations for [latex]y[/latex] in terms of [latex]x[/latex], and compare the results!
- Using the first point [latex]\left( {2,10} \right)[/latex] and slope [latex]m = – \,3[/latex]:

- Using the second point [latex]\left( {5,1} \right)[/latex] and slope [latex]m = – \,3[/latex]:
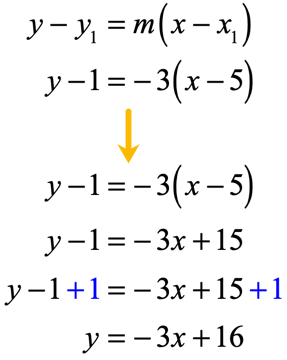
Therefore, it doesn’t matter which point you chose to construct the equation as long as the slope is the same, and the point selected must lie on the line.
Example 4: Determine the point-slope form of the line passing through the points [latex]\left( { – \,3, – \,5} \right)[/latex] and [latex]\left( {2, – \,15} \right)[/latex].
- Begin by solving the slope since two points are given. Let [latex]\left( { – \,3, – \,5} \right)[/latex] and [latex]\left( {2, – \,15} \right)[/latex] be the first and second point, respectively. This implies that their coordinates are as follow:
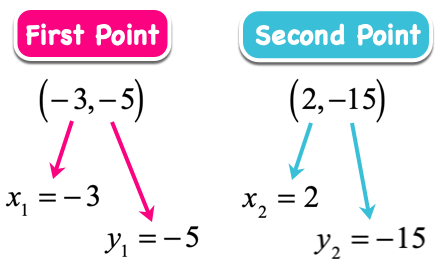
- Plug the values in the slope formula then simplify.
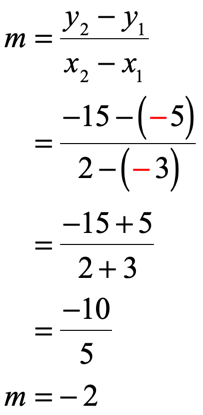
- The value of the slope is [latex]m = – \,2[/latex].
Write the point-slope in two ways, and show that they are equivalent equations.
Tip: Solve both equations for [latex]y[/latex] in terms of [latex]x[/latex], and compare the results!
- Using the first point [latex]\left( { – \,3, – \,5} \right)[/latex] and slope [latex]m = – \,2[/latex]:
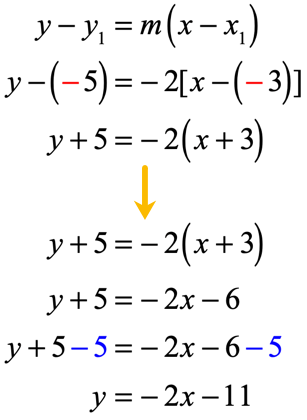
- Using the second point [latex]\left( {2, – \,15} \right)[/latex] and slope [latex]m = – \,2[/latex]:
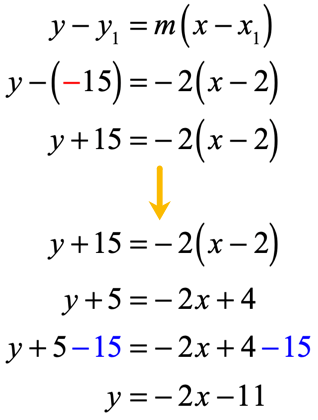
Again, you don’t need to write the point-slope using both of the two points. The purpose of this is to illustrate that any of the two points should work!
Example 5: Find the point-slope form of the line from its graph below.
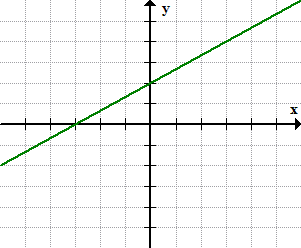
Solution:
Identify any point on the line. I think the most convenient is the [latex]y[/latex]-intercept of the line.
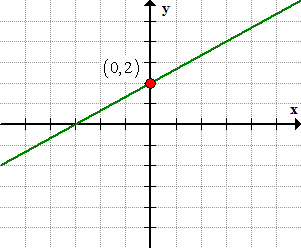
Next, find the slope graphically using the concept of “rise over run”, that is, [latex]m = {{rise} \over {run}}[/latex].
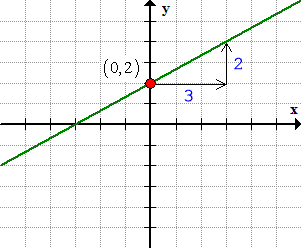
This gives us a slope of [latex]m = {{rise} \over {run}} = {2 \over 3}[/latex].
Now, we have a point at [latex]\left( {0,2} \right)[/latex] and a slope of [latex]m = {2 \over 3}[/latex] which should allow us to write the point-slope form of the line.
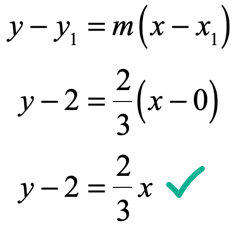
Example 6: Find the point-slope form of the line from its graph below.
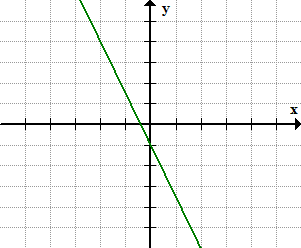
Solution:
Select any point on the line. Although it is okay to pick the [latex]y[/latex]-intercept at [latex]\left( {0, – \,1} \right)[/latex] , this time around, let’s choose a point not found on the [latex]y[/latex]-axis.
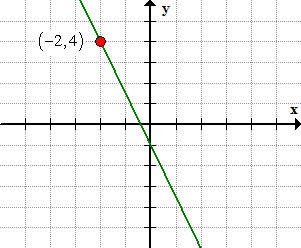
Next, find the slope graphically using the concept of “rise over run”, that is, [latex]m = {{rise} \over {run}}[/latex] .
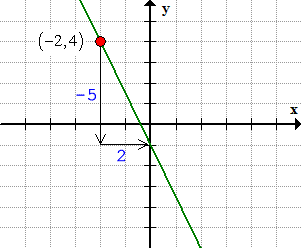
By moving in the downward direction in the [latex]y[/latex]-axis, the “rise” value should be negative. So the slope becomes [latex]m = {{rise} \over {run}} = {{ – \,5} \over 2}[/latex] .
We have a point at [latex]\left( { – \,2,4} \right)[/latex] and the slope of [latex]m = {{ – \,5} \over 2}[/latex]. Writing the point-slope form of the line
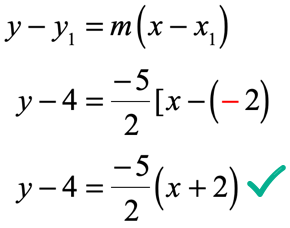
You may also be interested in these related math lessons or tutorials:
Types of Slopes of a Line
Slope Formula of a Line
Slope-Intercept Form of a Line
